INTRODUCTION

Les nombres complexes sont très importants en mathématiques du fait qu’ils constituent une extension de l’ensemble des nombres réels et permettent ainsi de formuler de nombreuses propositions de manière plus aisée et plus générale. Ils jouent également un rôle très important en sciences et dans les domaines technologiques, particulièrement en physique et en génie électrique [plus... La mécanique quantique repose entièrement sur les nombres complexes et, dans le domaine de l’électrotechnique,
la théorie du courant alternatif est grandement simplifiée en utilisant les nombres complexes]. Fort heureusement, les nombres complexes sont intégrés de base dans l’interpréteur Python qui contient des opérateurs permettant d’effectuer l’addition, la soustraction, la multiplication et la division de nombres complexes. De plus, le module cmath comporte de nombreuses fonctions acceptant des arguments complexes.

Les nombres complexes peuvent être représentés dans le plan complexe par de points ou des vecteurs. TigerJython permet d’utiliser une fenêtretortue, un canevas GPanel ou une grille de jeu JGameGrid pour représenter le plan complexe car toutes les fonctions de ces trois bibliothèques respectives demandant des paramètres de coordonnées (x, y) acceptent également des nombres complexes à la place de deux coordonnées réelles.

OPÉRATIONS ÉLÉMENTAIRES SUR LES NOMBRES COMPLEXES

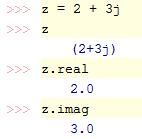
En Python, l’unité imaginaire est dénotée par le symbole j au lieu de i car c’est ainsi qu’il est noté la plupart du temps en génie électrique. Il y a plusieurs manières de définir un nombre complexe dont la partie réelle vaut 2 et la partie imaginaire vaut 3 :

Pour tester les exemples suivants et vous faire la main avec les nombres complexes, le mieux est d’utiliser la console TigerJython :

On peut obtenir la partie réelle et la partie imaginaire d’un nombre complexe grâce à z.real et z.imag respectivement. Il faut garder à l’esprit qu’il ne s’agit pas d’appels de méthodes mais que z.real et z.imag se comportent comme des variables de type float en lecture seule.

Le carré de l’unité imaginaire 1j est -1. En d’autres termes, l’unité imaginaire correspond à la racine de -1. Pour calculer la racine carrée d’un nombre complexe, il faut importer le module cmath au lieu du module math.

La fonction standard abs() retourne non seulement la valeur absolue d’un nombre entier ou flottant, mais également le module d’un nombre complexe. Les opérations élémentaires +, -, *, / et l’opérateur d’exponentiation ** sont également valables pour les nombres complexes. Ces opérations présentent les mêmes règles de précédence que dans le cas des nombres à virgule flottante.

Le programme suivant représente graphiquement les puissances du nombre complexe z = 0.9 + 0.3j dont le module est légèrement inférieur à 1. Puisque le module du produit de deux nombres complexes est donné par le produit de leur module et que l’argument (aussi appelé la phase) du produit est la somme des phases, les puissances de z vont former une spirale facilement représentable à l’aide de GPanel. Pensez à faire le remplissage de la spirale avant de dessiner le quadrillage car sinon, le quadrillage viendrait perturber le remplissage puisqu’il contribue à déterminer la zone fermée à colorier.

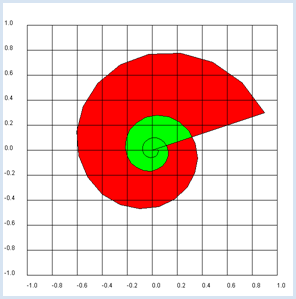
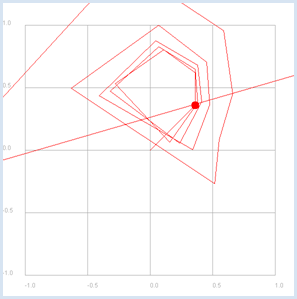
from gpanel import *
makeGPanel(-1.2, 1.2, -1.2, 1.2)
title("Complex plane")

z = 0.9 + 0.3j
for n in range(1, 60):
    y = z**n
    draw(y)
fill(0.2, 0, "white", "red")
fill(0.0, 0.2, "white", "green")
drawGrid(-1.0, 1.0, -1.0, 1.0)

MEMENTO

APPLICATIONS CONFORMES

Considérons maintenant des applications qui, à tout point P(x, y) du plan (pixel), associent un et un seul point (pixel) P'(x', y').

On peut également considérer les points du plan comme des nombres complexes et considérer les applications du plan dans lui-même comme des fonctions complexes qui, à tout nombre complexe z, associent un et un seul nombre complexe z’. On écrit donc  z' = f(z) Dans le programme suivant, on représente la fonction complexe z' = f(z) = 1/z (inversion) que l’on évalue sur l’ensemble des points formant une grille du plan complexe.

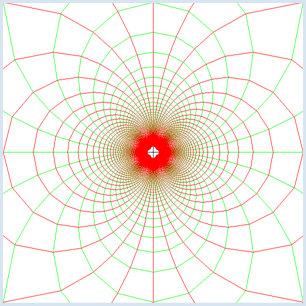
On choisit donc dans le plan complexe une plage entre -5 et 5 sur chacun des axes et on imagine un grillage constitué de 201 lignes horizontales et verticales distantes de 1/20 entre -5 et 5. On dessine en vert l’image par la fonction f des lignes horizontales et en rouge l’image des lignes verticales. On obtient ainsi une magnifique image permettant de mieux se représenter l’effet de la fonction f.

from gpanel import *

# function f(z) = 1/z
def f(z):
    if z == 0:
        return 0
    return 1 / z

min_value = -5.0
max_value = 5.0
step = 1 / 20
reStep = complex(step, 0)
imStep = complex(0, step)

makeGPanel(min_value, max_value, min_value, max_value)
title("Conformal mapping for f(z) = 1 / z")
line(min_value, 0, max_value, 0)  # Real axis
line(0, min_value, 0, max_value) # Imaginary axis

# Transform horizontal line per line
setColor("green")
z = complex(min_value, min_value)
while z.imag < max_value:
    z = complex(min_value, z.imag) # left
    move(f(z))
    while z.real < max_value: # move along horz. line
        draw(f(z))
        z = z + reStep
    z = z + imStep

# Transform vertical line per line
setColor("red")
z = complex(min_value, min_value)
while z.real < max_value:
    z = complex(z.real, min_value) # bottom
    move(f(z))
    while z.imag < max_value:  # move along vert. line
        draw(f(z))
        z = z + imStep
    z = z + reStep

MEMENTO

MANDELBROT FRACTALS

Nombreuses sont les personnes connaissant les fractales et vous avez sans doute déjà entendu parler de l’ensemble de Mandelbrot. Nous allons le représenter à l’aide d’un programme. De nombreux algorithmes permettant de représenter les fractales sont basés sur les nombres complexes, ce qui nous motive à travailler avec les nombres complexes en Python. Le père de la géométrie des fractales est Benoît Mandelbrot (1924-2010).

Mandelbrot lors du cours d’introduction de la Légion d'honneur (2006) (© Wiki)

Pour générer une fractale de Mandelbrot, on considère une suite de nombres complexes définie par un nombre complexe quelconque c et la relation de récurrence

z'  =  z²  +  c     avec le terme initial     z₀  =  0

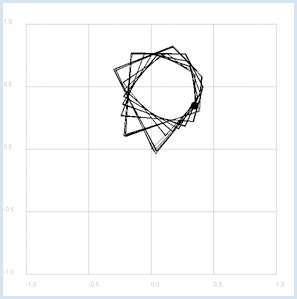
L’ensemble de Mandelbrot est formé de tous les nombres complexes c tels que la suite précédente est bornée.

Avant d’attaquer l’algorithme permettant de représenter l’ensemble de Mandelbrot, représentons les termes des suites définies par les nombres c1 = 0.35 + 0.35j et c2 = 0.36 + 0.36j.

On peut immédiatement constater que c1 appartient à l’ensemble de Mandelbrot et que c2 n’en fait pas partie.

from gpanel import *

def f(z):
    return z * z + c

makeGPanel(-1.2, 1.2, -1.2, 1.2)
title("Mandelbrot iteration")

drawGrid(-1, 1.0, -1, 1.0, 4, 4, "gray")

isMandelbrot = askYesNo("c in Mandelbrot set?")
if isMandelbrot:
    c = 0.35 + 0.35j
    setColor("black")
else:
    c = 0.36+ 0.36j
    setColor("red")

title("Mandelbrot iteration with c = " + str(c))
move(c)
fillCircle(0.03)

z = 0j
while True:
    if z == 0:
        move(z)
    else:
        draw(z)
    z = f(z)
    delay(100)         

from gpanel import *

def isInSet(c):
    z = 0
    for n in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return False
    return True

maxIterations = 50
R = 2
xmin = -2
xmax = 1
xstep = 0.03
ymin = -1.5
ymax = 1.5
ystep = 0.03

makeGPanel(xmin, xmax, ymin, ymax)
line(xmin, 0, xmax, 0)  # real axis
line(0, ymin, 0, ymax) # imaginary axis
title("Mandelbrot set")
y = ymin
while y <= ymax:
    x = xmin
    while x <= xmax:
        c = x + y*1j
        inSet = isInSet(c)
        if inSet:
            move(c)
            fillCircle(0.01)
        x += xstep
    y += ystep

Ce graphique permet déjà de déceler l’ensemble de Mandelbrot. On peut cependant encore obtenir de plus jolis graphiques si l’on représente en couleur les points c pour lesquels la suite des modules diverge. On choisira la couleur en fonction de la vitesse avec laquelle la suite définie par le point c diverge. On peut obtenir une bonne indication de cette vitesse de divergence en considérant le rang itCount du premier terme de la suite dont le module excède 2. Pour associer itCount à une couleur, on utilise la fonction getIterationColor() que vous pouvez bidouiller à votre convenance pour obtenir une magnifique image de fractale.

from gpanel import *

def getIterationColor(it):
    color = makeColor((30 * it) % 256, 
                      (4 * it) % 256, 
                      (255 - (30 * it)) % 256)
    return color
    
def mandelbrot(c):
    z = 0
    for it in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return it
    return maxIterations

maxIterations = 50
R = 2
xmin = -2
xmax = 1
xstep = 0.003
ymin = -1.5
ymax = 1.5
ystep = 0.003

makeGPanel(xmin, xmax, ymin, ymax)
title("Mandelbrot set")
enableRepaint(False)
y = ymin
while y <= ymax:
    x = xmin
    while x <= xmax:
        c = x + y*1j
        itCount = mandelbrot(c)
        if itCount == maxIterations: # inside Mandelbrot set
            setColor("black")
        else: # outside Mandelbrot set
           setColor(getIterationColor(itCount))
        point(c)
        x += xstep
    y += ystep
    repaint()
        

MEMENTO

EXERCICES

MATÉRIEL SUPPLÉMENTAIRE

COURANT ALTERNATIF ET IMPÉDANCE

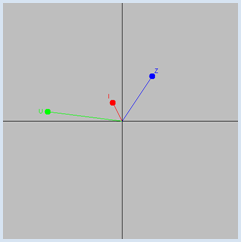
Les circuits électriques constitués de composants passifs (résistances, condensateurs, self) et traversés par des courants alternatifs peuvent être modélisés comme des circuits à courant continu si l’on utilise des valeurs complexes pour les tensions, les courants et les résistances. Une résistance complexe généralisée est appelée impédance et souvent désignée par Z ou par X lorsqu’il s’agit d’une impédance purement imaginaire (partie réelle nulle). L’impédance d’une résistance ohmique est R, celle d’une self X_L = jωL (inductance = self) et celle d’un condensateur est donnée par X_C = 1 / jωC (C: capacité), où ω = 2πf (f: fréquence).

Une tension alternative complexe u = u(t) parcourt un cercle du plan complexe de manière uniforme (vitesse angulaire constante). Si l’on applique cette tension aux bornes d’une impédance , le courant i(t) la traversant sera déterminé par la loi d’Ohm u = Z * i. Puisque lors de la multiplication deux nombres complexes, les arguments (phases) de deux nombres sont additionnés et les modules multipliés, le courant suit la tension avec un décalage de phase de Z:

phase(u) = phase(Z) + phase(i)

De ce fait, le courant i parcourt également un cercle du plan complexe. Les modules (amplitudes) sont donnés par :

| u | = | Z | * | i |

Le programme suivant représente cette relation dans le plan complexe en prenant les valeurs  | u | = 5V et Z = 2 +3j ainsi qu’une fréquence f = 10 Hz. Puisque le graphique serait complètement effacé, reconstitué et redessiné à chaque étape de l’animation en utilisant la fonction repaint(), on utilise plutôt un GPanel avec enableRepaint(False).

from gpanel import *
import math

def drawAxis():
   line(min, 0, max, 0)  # real axis
   line(0, min, 0, max) # imaginary axis


def cdraw(z, color, label):
    oldColor = setColor(color)
    line(0j, z)
    fillCircle(0.2)
    z1 = z + 0.5 * z / abs(z) - (0.1 + 0.2j)
    text(z1, label)
    setColor(oldColor)

min = -10
max = 10
dt = 0.001

makeGPanel(min, max, min, max)
enableRepaint(False)
bgColor("gray")
title("Complex voltages and currents")

f = 10 # Frequency
omega = 2 * math.pi * f

t = 0
uA = 5
Z = 2 + 3j

while True:
    u = uA * (math.cos(omega * t) + 1j * math.sin(omega * t))
    i = u / Z
    clear()
    drawAxis()
    cdraw(u, "green", "U")
    cdraw(i, "red", "I")
    cdraw(Z, "blue", "Z")
    repaint()
    t += dt
    delay(100)

MEMENTO

Cette connaissance est applicable à ce simple circuit constitué uniquement d’une résistance et d’un condensateur. On veut connaitre la tension u1 à sa sortie en fonction de la fréquence f pour des valeurs connues de la tension uo en entrée, de la résistance R et de la capacité C.

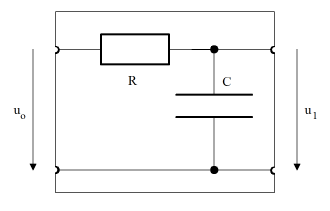
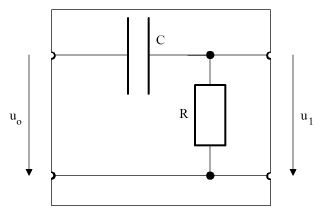
Le calcul est simple : la mise en série de la résistance R et du condensateur C donne lieu à l’impédance Z = R + X_Cet, de ce fait, au courant i = uo / Z. On obtient la tension de sortie en utilisant la loi d’Ohm généralisée :

u1 = Xc * i =

(  Xc  )/ R + Xc

* u0 =

our

u1 = v * u0

avec

v =

(  Xc  )/ R + Xc

La grandeur complexe v est appelée gain du circuit électrique. On peut la visualiser dans le plan complexe pour différentes valeurs de f et l’on observe alors que le gain vaut 1 pour une fréquence nulle (courant continu) et que ce gain va diminuer jusqu’à attendre 0 lorsqu’on augmente la fréquence de la tension. De ce fait, un tel circuit transmet bien les basses fréquences mais atténue les hautes fréquences. On parle de filtre passe-bas.

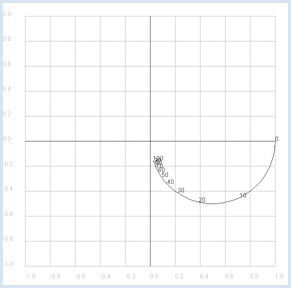
from gpanel import *
from math import pi

def drawAxis():
   line(-1, 0, 1, 0)  # Real axis
   line(0, -1, 0, 1) # Imaginary axis

makeGPanel(-1.2, 1.2, -1.2, 1.2)
drawGrid(-1.0, 1.0, -1.0, 1.0, "gray")
setColor("black")
drawAxis()
title("Complex gain factor – low pass")

R = 10
C = 0.001
def v(f):
    if f == 0:
        return 1 + 0j
    omega = 2 * pi * f
    XC = 1 / (1j * omega * C)
    return XC / (R + XC)

f = 0 # Frequency
while f <= 100:
    if f == 0:
        move(v(f))
    else:
        draw(v(f))
    if f % 10 == 0:
        text(str(f)) 
    f += 1
    delay(10)
    

Un diagramme de Bode est constitué de deux graphiques. Dans le premier, on représente l’amplitude du gain en fonction de la fréquence et dans le second, on représente sa phase en fonction de la fréquence. On utilise généralement des échelles logarithmiques.

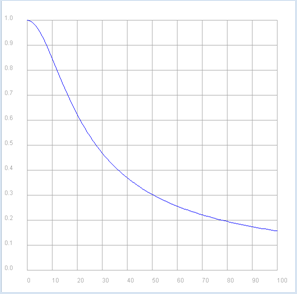
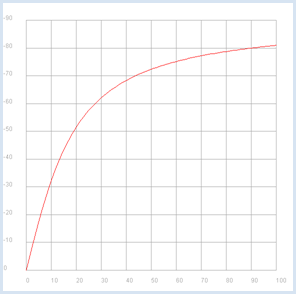
from gpanel import *
import math
import cmath

R = 10
C = 0.001

def v(f):
    if f == 0:
        return 1 + 0j
    omega = 2 * math.pi * f
    XC = 1 / (1j * omega * C)
    return XC / (R + XC)

p1 = GPanel(-10, 110, -0.1, 1.1)
drawPanelGrid(p1, 0, 100, 0, 1.0, "gray")
p1.title("Bode Plot - Low Pass, Gain")
p1.setColor("blue")
f = 0
while f <= 100:
    if f == 0:
        p1.move(f, abs(v(f)))
    else:
        p1.draw(f, abs(v(f)))
    f += 1

p2 = GPanel(-10, 110, 9, -99)
drawPanelGrid(p2, 0, 100, 0, -90, 10, 9, "gray")
p2.title("Bode Plot - Low Pass, Phase")
p2.setColor("red")
f = 0
while f <= 100:
    if f == 0:
        p2.move(f, math.degrees(cmath.phase(v(f))))
    else:
        p2.draw(f, math.degrees(cmath.phase(v(f))))
    f += 1    

MEMENTO

EXERCICES