deutsch     english    français     Imprimer

 

8.6 CORRÉLATION, RÉGRESSION

 

 

INTRODUCTION

 

Aussi bien en sciences naturelles que dans la vie de tous les jours, les collections de données sous forme de mesures jouent un rôle important. Il n’est cependant pas toujours nécessaire d’avoir recours à un instrument de mesure. Les données peuvent en effet également provenir d’un sondage lié à une étude statistique. Suite à une collecte de données, il est très important d’interpréter les données collectées. L’interprétation des données peut conduire à une affirmation qualitative, par exemple que les valeurs augmentent ou diminuent avec le temps. Elle peut également permettre de vérifier expérimentalement un résultat scientifique théorique.

Une des difficultés majeures réside dans le fait que les mesures sont toujours sujettes à certaines fluctuations et ne sont jamais parfaitement reproductibles. Malgré ces incertitudes inhérentes aux mesures, le responsable d’une telle étude doit tout de même parvenir à des conclusions scientifiquement correctes. Les incertitudes de mesure ne proviennent pas nécessairement des instruments de mesure eux-mêmes car elles peuvent également provenir de la nature même de l’expérience. Par exemple, la « mesure » des résultats obtenus lors de jets de dés conduit à des valeurs dispersées entre 1 et 6. De ce fait, pour tout type de mesures, les considérations statistiques jouent un rôle central.

Très souvent, des variables x et y sont mesurées de pair dans une série de mesures et l’on se pose la question de savoir si elles sont corrélées (reliées) et si ces mesures présentent une certaine régularité. On appelle visualisation de données le fait de représenter les couples de mesures (x, y) comme des points dans un repère cartésien. On peut presque toujours reconnaître, à la simple vue de ce graphique, si les variables x et y sont dépendantes l’une de l’eau : il suffit d’observer à ce dessin la distribution des valeurs mesurées.

CONCEPTS DE PROGRAMMATION:
Visualisation de données, distribution de la grandeur mesurée, nuage de points, bruit, covariance, coefficient de corrélation, régression

 

 

VISUALISATION DE DONNÉES DÉPENDANTES ET INDÉPENDANTES

 


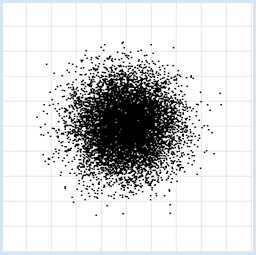
On peut aisément se représenter des données indépendantes dans un diagramme x-y en prenant pour x et y des nombres aléatoires uniformément distribués. Bien que cela ne soit pas nécessaire dans ce cas précis, on copie les valeurs mesurées dans les listes xval et yval avant de les représenter comme des points (x,y).

   


from random import random
from gpanel import *

z = 10000
    
makeGPanel(-1, 11, -1, 11)
title("Uuniformly distributed value pairs")
drawGrid(10, 10, "gray")

xval = [0] * z
yval = [0] * z

for i in range(z):
    xval[i] = 10 * random()
    yval[i] = 10 * random()
    move(xval[i], yval[i])
    fillCircle(0.03)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)


On obtient des graphiques en forme de galaxies lorsque les valeurs x et y sont indépendantes mais distribuées selon une loi normale autour d’une valeur moyenne. Dans l’exemple ci-contre, on a pris 5 comme valeur moyenne et 1 comme paramètre de dispersion. On appelle ce genre de graphique un nuage de points.

Il est très facile d’obtenir une série de nombres aléatoires suivant une loi normale (également appelée gaussienne) en Python avec la fonction random.gauss(valeur_moyenne, dispersion).

 

   

from random import gauss
from gpanel import *

z = 10000
    
makeGPanel(-1, 11, -1, 11)
title("Normally distributed value pairs")
drawGrid(10, 10, "gray")

xval = [0] * z
yval = [0] * z

for i in range(z):
    xval[i] = gauss(5, 1)
    yval[i] = gauss(5, 1)
    move(xval[i], yval[i])
    fillCircle(0.03)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)


On peut facilement simuler une relation de dépendance entre deux variables x et y. Pour ce faire, prenons pour x une série de valeurs équidistantes en parcourant un intervalle par incréments réguliers et, pour chaque x, calculons y en fonction de x en ajoutant une petite fluctuation statistique. En physique, de telles fluctuations sont appelées bruit.

Le programme suivant représente le nuage de points pour x = 0..10 avec un incrément de 0.01 et la fonction y = -x * (0.2 * x - 2) avec un bruit suivant une loi normale.

 

   

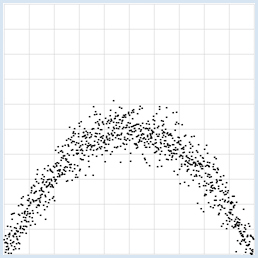
from random import gauss
from gpanel import *
import math

z = 1000
a = 0.2
b = 2

def f(x):
    y = -x * (a * x - b)
    return y

makeGPanel(-1, 11, -1, 11)
title("y = -x * (0.2 * x - 2) with normally distributed noise")
drawGrid(0, 10, 0, 10, "gray")

xval = [0] * z
yval = [0] * z

for i in range(z):
    x = i / 100
    xval[i] = x
    yval[i] = f(x) + gauss(0, 0.5)
    move(xval[i], yval[i])
    fillCircle(0.03)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

On peut facilement reconnaître des relations de dépendance entre variables aléatoires grâce à la visualisation de données [plus... L’exemple précédent est très connu car la relation de dépendance entre les variables n’est pas détectée la mesure de dépendance introduite ci-après (covariance)].

Avec une série de nombres aléatoires distribués de manière uniforme sur un intervalle [a, b], les nombres apparaissent avec la même fréquence dans chaque sous-intervalle de même longueur. Une distribution normale de nombres aléatoires (ou gaussienne) présente une forme de cloche et présente la particularité que 68% des valeurs se trouvent dans l’intervalle [moyenne – dispersion ; moyenne + dispersion].

 

 

LA COVARIANCE COMME MESURE DE LA DÉPENDANCE DE DEUX VARIABLES ALÉATOIRES

 

En plus de vouloir rendre visible la dépendance entre deux variables grâce à un graphique, on veut pouvoir mesurer ce degré de dépendance par un nombre. Partons d’un exemple concret en considérant un double jet de dé où x est le résultat du premier jet et y le résultat du second. Effectuons cette expérience de nombreuses fois en représentant les paires de valeur dans un nuage de points. Puisque les deux valeurs x et y sont indépendantes, on obtient un nuage de points régulier. Si l’on calcule l’espérance de x et y, on obtient le résultat bien connu de 3.5.

  

Puisque les variables x et y sont indépendantes, la probabilité pxy d’obtenir la paire (x, y) lors d’un double jet est donnée par pxy = px * py. Il n’y a qu’un pas pour faire l’hypothèse que cette règle du produit des probabilités est valable de manière générale lorsque les variables x et y sont indépendantes.

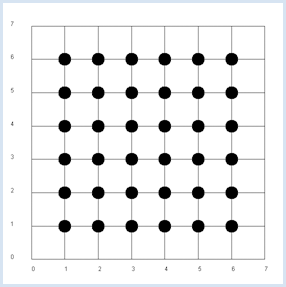
Lorsque les variables x et y sont indépendantes, l’espérance mathématique du produit x*y est donnée par le produit des espérances de x et y [plus... La preuve théorique n’est pas très compliquée:

] .

La simulation suivante confirme cette hypothèse : 

from random import randint
from gpanel import *

z = 10000 # number of double rolls

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

makeGPanel(-1, 8, -1, 8)
title("Double rolls. Independent random variables")
addStatusBar(30)
drawGrid(0, 7, 0, 7, 7, 7, "gray")

xval =  [0] * z
yval =  [0] * z
xyval = [0] * z

for i in range(z):
    a = randint(1, 6)
    b = randint(1, 6)
    xval[i] = a
    yval[i] = b
    xyval[i] = xval[i] * yval[i]
    move(xval[i], yval[i])
    fillCircle(0.2)

xm = mean(xval)
ym = mean(yval)
xym = mean(xyval)
setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  E(x, y) = " + dec2(xym))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 
 

MEMENTO

 

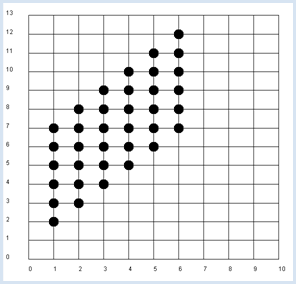
Il est conseillé d’utiliser la barre d’état pour écrire le résultat de la simulation. La fonction dec2() arrondit le résultat à deux chiffres et le retourne sous forme de chaîne de caractères.

Les valeurs sont bien entendu sujettes aux fluctuations statistiques.

Dans la prochaine simulation, nous continuons d’examiner des paires de valeurs (x,y) lors de deux jets successifs d’un dé mais cette fois-ci, x représentera le résultat obtenu lors du premier jet et y la somme des deux jets successifs. Dans cette nouvelle situation, il est clair que y est dépendante de x puisque, par exemple, si x=1, la probabilité d’obtenir 4 pour y n’est pas la même que si x=2. 

 

La simulation suivante confirme que la règle du produit ne s’applique pas lorsque les variables x et y sont dépendantes. Il est de ce fait raisonnable d’introduire l’écart avec la règle du produit, à savoir la différence

c = E(x*y) - E(x)*E(y)

comme une mesure de la dépendance entre x et y. On appelle cette grandeur la covariance.

En même temps, on voit dans le programme que la covariance peut également être calculée comme la somme des carrés des écarts avec la moyenne.

 

   

from random import randint
from gpanel import *

z = 10000 # number of double rolls

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n
    
makeGPanel(-1, 11, -2, 14)
title("Double rolls. Independent random variables")
addStatusBar(30)
drawGrid(0, 10, 0, 13, 10, 13, "gray")

xval =  [0] * z
yval =  [0] * z
xyval = [0] * z

for i in range(z):
    a = randint(1, 6)
    b = randint(1, 6)
    xval[i] = a
    yval[i] = a + b
    xyval[i] = xval[i] * yval[i]
    move(xval[i], yval[i])
    fillCircle(0.2)

xm = mean(xval)
ym = mean(yval)
xym = mean(xyval)
c = xym - xm * ym
setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  E(x, y) = " + dec2(xym) + \
          ",  c = " + dec2(c) + \
          ",  covariance = " + dec2(covariance(xval, yval)))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

On obtient environ 2,9 pour la covariance des valeurs obtenues dans cette simulation. La covariance est une bonne mesure de la dépendance entre deux variables aléatoires.

 

 

LE COEFFICIENT DE CORRÉLATION

 

La covariance que nous venons d’introduire présente également un désavantage. Selon l’échelle des valeurs de x et y mesurées, la covariance livre des grandeurs différentes même si les grandeurs présentent le même degré de dépendance. On peut le voir facilement si l’on refait la même expérience avec des dés dont les faces valent 10, 20, 30, 40, 50, 60 au lieu de 1, 2, 3, 4, 5, 6. La covariance va alors beaucoup changer bien que le degré de dépendance entre x et y soit dans ce cas exactement le même qu’avec un dé habituel. Ceci justifie l’introduction d’une covariance normalisée, appelée coefficient de corrélation, obtenue en divisant la covariance par la dispersion statistique des valeurs x et y :

  correlation coefficient(x, y) = (         covariance(x, y)        )/ dispersion(x) * dispersion(y)  

Le coefficient de corrélation est toujours compris entre -1 et 1. Une valeur 0 correspond à l’absence de dépendance et une valeur proche de 1 en valeur absolue à une grande dépendance entre les variables x et y. Lorsque le coefficient est proche de 1, les variables sont dépendantes et les valeurs de y augmentent lorsque x augmente. Lorsque le coefficient de corrélation est proche de -1, les valeurs de y diminuent lorsque x augmente.

Reconduisons l’expérience du double jet en étudiant le degré de dépendance entre les deux jets. 

from random import randint
from gpanel import *
import math

z = 10000 # number of double rolls
k = 10 # scalefactor

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval) / (deviation(xval) * deviation(yval))
    
makeGPanel(-1 * k, 11 * k, -2 * k, 14 * k)
title("Double rolls. Independent random variables.")
addStatusBar(30)
drawGrid(0, 10 * k, 0, 13 * k, 10, 13, "gray")

xval =  [0] * z
yval =  [0] * z
xyval = [0] * z

for i in range(z):
    a = k * randint(1, 6)
    b = k * randint(1, 6)
    xval[i] = a
    yval[i] = a + b
    xyval[i] = xval[i] * yval[i]
    move(xval[i], yval[i])
    fillCircle(0.2 * k)

xm = mean(xval)
ym = mean(yval)
xym = mean(xyval)
c = xym - xm * ym
setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  E(x, y) = " + dec2(xym) + \
          ",  covariance = " + dec2(covariance(xval, yval)) + \
          ",  correlation = " + dec2(correlation(xval, yval)))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 
 

MEMENTO

 

Même en modifiant le facteur d’échelle k de la valeur des faces du dé, le coefficient de corrélation va rester aux alentours de 0.71 au contraire de la covariance qui va beaucoup changer en conséquence [plus... Le coefficient de corrélation ne mesure que la dépendance linéaire des variables. De ce fait, il n’est pas capable de mesurer correctement la relation de dépendance entre deux variables si cette dépendance n’est pas linéaire. C’est le cas par exemple dans l’exemple quadratique développé plus haut].

Au lieu de parler de coefficient de corrélation, on peut aussi simplement utiliser le terme corrélation.

 

 

MEDICAL RESEARCH PUBLICATION

 

Grâce aux connaissances développées dans ce chapitre, vous êtes déjà capables de comprendre et d’évaluer une publication scientifique publiée dans la prestigieuse revue " New England Journal of Medicine " [plus... FH Messerli, Chocolate Comsumption, Cognitive Function, and Nobel Laureates,
The New England Journal of Medicine 367; 16 (Oct. 2012)]. Celle-ci cherche à savoir s’il y a un lien entre la consommation de chocolat et le nombre de prix Nobel dans différents pays industrialisés. Autrement dit, cette étude cherche à savoir si l’intelligence et la consommation de chocolat sont corrélées d’une quelconque manière. L’étude s’appuie sur les données suivantes librement disponibles sur le Web:

  

Prix Nobel :
http://en.wikipedia.org/wiki/List_of_countries_by_Nobel_laureates_per_capita

Consommation de chocolat :
http://www.chocosuisse.ch/web/chocosuisse/en/documentation/facts_figures.html
http://www.theobroma-cacao.de/wissen/wirtschaft/international/konsum

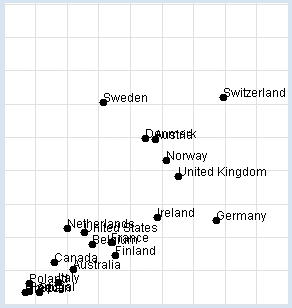
On aimerait reproduire l’étude en utilisant un programme informatique qui utilise une liste data contenant des sous-listes de trois éléments : le nom du pays, le nombre de kilogrammes de chocolat consommés annuellement par habitant et le nombre de prix Nobel par tranche de 10 millions d’habitants. Le programme représente les données graphiquement et détermine le coefficient de corrélation entre les deux grandeurs (consommation de chocolat et nombre de prix Nobel. 

from gpanel import *
import math

data = [["Australia", 4.8, 5.141],
        ["Austria", 8.7, 24.720],
        ["Belgium", 5.7, 9.005],
        ["Canada", 3.9, 6.253],
        ["Denmark", 8.2, 24.915],
        ["Finland", 6.8, 7.371],
        ["France", 6.6, 9.177],
        ["Germany", 11.6, 12.572],
        ["Greece", 2.5, 1.797],
        ["Italy", 4.1, 3.279],
        ["Ireland", 8.8, 12.967],
        ["Netherlands", 4.5, 11.337],
        ["Norway", 9.2, 21.614],
        ["Poland", 2.7, 3.140],
        ["Portugal", 2.7, 1.885],
        ["Spain", 3.2, 1.705],
        ["Sweden", 6.2, 30.300],
        ["Switzerland", 11.9, 30.949],
        ["United Kingdom", 9.8, 19.165],
        ["United States", 5.3, 10.811]]

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval) / (deviation(xval) * deviation(yval))

makeGPanel(-2, 17, -5, 55)
drawGrid(0, 15, 0, 50, "lightgray")

xval = []
yval = []

for country in data:
    d = country[1]
    v = country[2]
    xval.append(d)
    yval.append(v)   
    move(d, v)
    fillCircle(0.2)
    text(country[0])

title("Chocolate-Brainpower-Correlation: " + dec2(correlation(xval, yval)))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 
 

MEMENTO

 

L’étude fournit un coefficient de corrélation d’environ 0.71, ce qui est assez élevé. Il faut cependant prendre du recul pour réaliser que ce résultat peut être interprété de diverses manières. Les deux jeux de données sont manifestement corrélés mais les causes de cette corrélation ne sont pas claires et restent du domaine de la spéculation. Cette étudie ne constitue en aucun cas une preuve que la consommation de chocolat rend plus intelligent. De manière générale, lorsque les grandeurs x et y sont fortement corrélées, il se peut que x soit la cause de y ou l’inverse. Dans notre cas, il se peut que les gens soient plus intelligents parce qu’ils consomment plus de chocolat mais il se peut aussi qu’ils consomment plus de chocolat parce qu’ils sont plus intelligents. Le résultat peut encore être interprété de manière complètement différente si l’on considère que les deux grandeurs sont certainement toutes deux des conséquences d’autres grandeurs non prises en compte dans l’étude.

Prenez le temps de discuter du sens et du but d’une telle étude avec d’autres personnes de votre entourage en vous intéressant à leur opinion sur le sujet.

 

 

ERREURS DE MESURE ET BRUIT

 

Même si la relation entre x et y est parfaitement connue, des erreurs de mesure ou d’autres influences peuvent faire fluctuer les valeurs mesurées. Dans la simulation suivante, on considère une relation linéaire entre x et y où les valeurs y sont sujettes à des fluctuations obéissant à une loi normale. 

La simulation détermine le coefficient de corrélation entre x et y et entoure le point de coordonnées (xm, ym) où xm et ym correspondent à l’espérance mathématique de x et y. 

 

 

   

from random import gauss
from gpanel import *
import math

z = 1000
a = 0.6
b = 2
sigma = 1

def f(x):
    y = a * x + b
    return y

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval) / (deviation(xval) * deviation(yval))
    
makeGPanel(-1, 11, -1, 11)
title("y = 0.6 * x + 2 normally distributed measurement errors")
addStatusBar(30)
drawGrid(0, 10, 0, 10, "gray")
setColor("blue")
lineWidth(3)
line(0, f(0), 10, f(10))

xval = [0] * z
yval = [0] * z

setColor("black")
for i in range(z):
    x = i / 100
    xval[i] = x
    yval[i] = f(x) + gauss(0, sigma)
    move(xval[i], yval[i])
    fillCircle(0.03)

xm = mean(xval)
ym = mean(yval)
move(xm, ym)
circle(0.5)

setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  correlation = " + dec2(correlation(xval, yval)))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

On voit, comme attendu, que la simulation donne un coefficient de corrélation élevé. Il devient d’ailleurs de plus en plus élevé à mesure que l’on réduit le paramètre de dispersion sigma. La corrélation vaut exactement 1 pour sigma = 0. De plus, le point ayant pour coordonnées les espérances P(0.5, 0.5) est situé sur la droite.

 

 

DROITE DE RÉGRESSION, MEILLEUR AJUSTEMENT

 

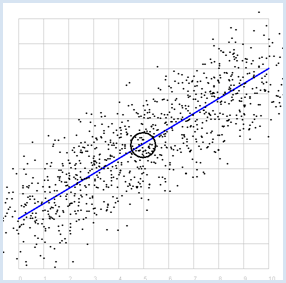
Dans l’exemple précédent, on a engendré un nuage de points en ajoutant artificiellement du bruit sur des données correspondant à la base parfaitement à un modèle linéaire. Nous allons maintenant considérer le cas inverse : comment retrouver la droite parfaite qui approxime le mieux un nuage de points résultant de données suivant un modèle linéaire mais entachées d’erreurs ? La droite recherchée est appelée droite de régression.

Nous savons déjà au moins une chose importante : la droite de régression passe par le point P dont les coordonnées correspondent à l’espérance de x et de y. Pour la déterminer complètement, on peut procéder de la manière suivante :

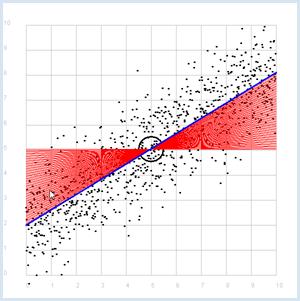
On trace une droite quelconque passant par le point P et l’on détermine, pour toutes les mesures x, les carrés des distances verticales entre les yi = f(xi) et la valeur mesurée pour ce même x. On détermine la somme de ces erreurs en additionnant tous les carrés de écarts.

On peut ensuite déterminer la meilleure droite de régression dans la simulation en faisant progressivement tourner la droite de test autour du point P et en calculant à chaque fois la somme des carrés des erreurs qui va alors diminuer. Dès que cette erreur se remet à augmenter, on sait que la droite précédente était le meilleur ajustement recherché.

 

   

from random import gauss
from gpanel import *
import math

z = 1000
a = 0.6
b = 2

def f(x):
    y = a * x + b
    return y

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

sigma = 1
    
makeGPanel(-1, 11, -1, 11)
title("Simulate data points. Press a key...")
addStatusBar(30)
drawGrid(0, 10, 0, 10, "gray")
setStatusText("Press any key")

xval = [0] * z
yval = [0] * z

for i in range(z):
    x = i / 100
    xval[i] = x 
    yval[i] = f(x) + gauss(0, sigma)
    move(xval[i], yval[i])
    fillCircle(0.03)

getKeyWait()
xm = mean(xval)
ym = mean(yval)
move(xm, ym)
lineWidth(3)
circle(0.5)

def g(x):
    y = m * (x - xm) + ym
    return y

def errorSum():
    count = 0
    for i in range(z):
        x = i / 100
        count += (yval[i] - g(x)) * (yval[i] - g(x))
    return count

m = 0
setColor("red")
lineWidth(1)
error_min = 0
while m < 5:
    line(0, g(0), 10, g(10))
    if m == 0:
        error_min = errorSum()
    else:
        if errorSum() < error_min:
            error_min = errorSum()
        else:
            break
    m += 0.01

title("Regression line found")
setColor("blue")
lineWidth(3)
line(0, g(0), 10, g(10))
setStatusText("Found slope: " +  dec2(m) + \
               ", Theory: " + dec2(covariance(xval, yval) 
              /(deviation(xval) * deviation(xval))))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

Au lieu d’utiliser une simulation informatique pour déterminer la droite de régression qui donne le meilleur ajustement, on peut également calculer sa pente grâce à la formule

  m = (covariance(x, y))/ dispersion(x)2  

Puisque la droite de régression passe par le point P de coordonnées E(x) et E(y), elle est donnée par l’équation cartésienne :

y - E(y) = m * (x - E(x))

 

 

EXERCICES

 

1.
La célèbre loi d’Engel issue des sciences économiques stipule qu’en moyenne, lorsque le revenu des ménages augmente, le montent mensuel absolu dépensé pour la nourriture augmente mais que ce montant diminue relativement aux autres dépenses.
a. Visualiser la relation entre le revenu et les dépenses totales pour la nourriture
b. Faire de même pour la relation entre le revenu et les dépenses relatives pour la nourriture
c. Déterminer le coefficient de corrélation entre le revenu et les dépenses absolues pour la nourriture
d. Déterminer la droite de régression entre le revenu et les dépenses absolues pour la nourriture en utilisant les données ci-dessous

Data:
Revenu mensuel
4000
4100
4200
4300
4400
4500
4600
4700
4800
4900
Dépenses%
64
63.25
62.55
61.90
61.30
60.75
60.25
59.79
59.37
58.99

5000
5100
5200
5300
5400
5500
5600
5700
5800
5900
6000
58.65
58.35
58.08
57.84
57.63
57.45
57.30
57.17
57.06
56.97
56.90

 
2.

L’histoire évolutionniste de l’univers acceptée par la communauté scientifique présuppose que tout a commencé il y a très longtemps par un Big Bang et que, depuis lors, l’univers est en expansion. La question principale est de savoir à quand remonte le Big Bang ou, autrement dit, quel est l’âge de l’univers. L’astronome Hubble a publié une fameuse étude en 1929 dans laquelle il montre qu’il y a une relation linéaire entre la distance d séparant les galaxies et leur vitesse d’éloignement v. La loi de Hubble est formulée de la manière suivante :

v = H * d

où H est la constante de Hubble.

On peut comprendre le processus de pensée des astrophysiciens en partant de données suivantes produites par le télescope spatial Hubble.

Galaxie

Distance
 [Mpc)

Vetesse
[km/s]

NGC0300

2

133

NGC095

9.16

664

NGC1326A

16.14

1794

NGC1365

17.95

1594

NGC1425

21.88

1473

NGC2403

3.22

278

NGC2541

11.22

714

NGC2090

11.75

882

NGC3031

3.63

80

NGC3198

13.8

772

NGC3351

10

642

NGC3368

10.52

768

NGC3621

6.64

609

NGC4321

15.21

1433

NGC4414

17.7

619

NGC4496A

14.86

1424

NGC4548

16.22

1384

NGC4535

15.78

1444

NGC4536

14.93

1423

NGC4639

21.98

1403

NGC4725

12.36

1103

IC4182

4.49

318

NGC5253

3.15

232

NGC7331

14.72

999

1 Megaparsec (Mpc) = 3.09 * 1019km

a)

Représenter ces données dans un nuage de points et les copier dans la liste data au sein du programme.

data = [
["NGC0300", 2.00, 133],
["NGC095", 9.16, 664],
["NGC1326A", 16.14, 1794],
["NGC1365", 17.95, 1594],
["NGC1425", 21.88, 1473],
["NGC2403", 3.22, 278],
["NGC2541", 11.22, 714],
["NGC2090", 11.75, 882],
["NGC3031", 3.63, 80],
["NGC3198", 13.80, 772],
["NGC3351", 10.0, 642],
["NGC3368", 10.52, 768],
["NGC3621", 6.64, 609],
["NGC4321", 15.21, 1433],
["NGC4414", 17.70, 619],
["NGC4496A", 14.86, 1424],
["NGC4548", 16.22, 1384],
["NGC4535", 15.78, 1444],
["NGC4536", 14.93, 1423],
["NGC4639", 21.98, 1403],
["NGC4725", 12.36, 1103],
["IC4182", 4.49, 318],
["NGC5253", 3.15, 232],
["NGC7331", 14.72, 999]]

Données tirées de Freedman et al, The Astrophysical Journal, 553 (2001)
b) Montrer que les données sont bien corrélées et déterminer la pente H de la droite de régression.
c) En supposant que la vitesse v d’une certaine galaxie demeure constante, sa distance est alors donnée par d = v * T, où T est l’âge de l’univers. On peut donc utiliser la loi de Hubble (v = H*d) pour estimer l’âge de l’univers puisque T = 1 / H. Déterminer l’âge de l’univers T donné par ce modèle linéaire.
.

 

 

 

MATÉRIEL SUPPLÉMENTAIRE


 

DÉTECTER DES INFORMATIONS CACHÉES EN UTILISANT L’AUTOCORRÉLATION

 

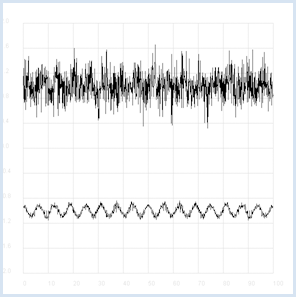
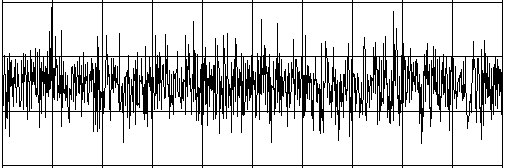
Des êtres intelligents habitant sur une autre planète désirent contacter d’autres êtres vivants en émettant des signaux radio présentant une certaine régularité (vous pouvez vous imaginez une sorte de code morse). L’intensité du signal faiblit au fur et à mesure de son voyage aux confins de l’univers s’en retrouve masqué par un bruit présentant des fluctuations statistiques. Le signal est capté sur terre à l’aide d’un radiotélescope qui ne révèle plus que du bruit.

Les statistiques et un programme informatique peuvent nous permettre de reconstituer le signal original. Si l’on calcule le coefficient de corrélation du signal avec lui-même mais décalé dans le temps, on peut réduire la part du bruit dans le signal. La corrélation d’une grandeur avec elle-même est appelée autocorrélation. On peut simuler ces propriétés importantes pour le traitement de signal à l’aide d’un programme Python.

Le signal utile original est une fonction sinusoïdale sur laquelle on superpose du bruit en ajoutant à chaque valeur de l’échantillon un nombre aléatoire selon une loi normale. Le programme ci-dessous commence par représenter le signal comportant le bruit aléatoire dans la partie supérieure de l’écran et attend que l’utilisateur presse une touche du clavier. On peut constater que le signal n’est plus reconnaissable.

Dans un deuxième temps, le programme construit l’autocorrélation du signal avec lui-même et représente l’évolution du coefficient de corrélation dans la partie inférieure du graphe. Le signal utile original sera à nouveau clairement reconnaissable.

  


from random import gauss
from gpanel import *
import math

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval)/(deviation(xval)*deviation(yval))
def shift(offset):
    signal1 = [0] * 1000
    for i in range(1000):
       signal1[i] = signal[(i + offset) % 1000]
    return signal1

makeGPanel(-10, 110, -2.4, 2.4)
title("Noisy signal. Press a key...")
drawGrid(0, 100, -2, 2.0, "lightgray")

t = 0
dt = 0.1
signal = [0] * 1000
while t < 100:
    y = 0.1 * math.sin(t) # Pure signal
#    noise = 0
    noise = gauss(0, 0.2)
    z = y + noise
    if t == 0:
        move(t, z + 1)
    else:
        draw(t, z + 1)
    signal[int(10 * t)] = z
    t += dt

getKeyWait()
title("Signal after autocorrelation")
for di in range(1, 1000):
    y = correlation(signal, shift(di))
    if di == 1:
        move(di / 10, y - 1)
    else:
        draw(di / 10, y - 1)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

Pour rendre cela encore plus tangible, commencez par écouter un rendu sonore du signal bruité puis du signal reconstitué par l’autocorrélation. Pour ce faire, il faudra vous replonger dans le chapitre traitant du on son. 

from soundsystem import *
import math
from random import gauss
from gpanel import *

n = 5000

def mean(xval):
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, k):
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (xval[(i + k) % n] - xm)
    return cxy / n

def deviation(xval):
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

makeGPanel(-100, 1100, -11000, 11000)
drawGrid(0, 1000, -10000, 10000)
title("Press <SPACE> to repeat. Any other key to continue.")

signal = []
for i in range(5000):
    value = int(200 *  (math.sin(6.28 / 20 * i) + gauss(0, 4)))
    signal.append(value)
    if i == 0:
        move(i, value + 5000)
    elif i <= 1000:
        draw(i, value + 5000)

ch = 32
while ch == 32:
    openMonoPlayer(signal, 5000)
    play()
    ch = getKeyCodeWait()

title("Autocorrelation running. Please wait...")
signal1 = []
xm = mean(signal)
sigma = deviation(signal)
q = 20000 / (sigma * sigma)
for di in range(1, 5000):
    value = int(q *  covariance(signal, di))
    signal1.append(value)
title("Autocorrelation Done. Press any key to repeat.")
for i in range(1, 1000):
    if i == 1:
        move(i, signal1[i] - 5000)
    else:
        draw(i, signal1[i] - 5000)

while True:
    openMonoPlayer(signal1, 5000)
    play()
    getKeyCodeWait()

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 
 

MEMENTO

 

Au lieu d’exécuter le programme, vous pouvez également écouter les deux signaux sonores en les téléchargeant au format WAV :

Signal bruité (cliquer ici)

Signal désiré (cliquer ici)