8.10 MARCHE ALÉATOIRE
![]()
INTRODUCTION |
Dans la vie quotidienne, de nombreux phénomènes sont déterminés par le hasard et il est souvent nécessaire de prendre des décisions sur la base de probabilités. On pourrait par exemple être amenés à préférer un mode de transport à un autre sur la base de leur probabilité respective d’être impliqué dans un accident. Dans de telles situations, l’ordinateur peut se révéler être un outil important permettant d’examiner les dangers potentiels à l’aide simulations, en ne prenant absolument aucun risque. Imaginons qu’une personne se soit perdue et qu’elle ne trouve plus le chemin pour rentrer à la maison. Elle va se mettre à effectuer une marche aléatoire consistant à se déplacer d’une même distance à chaque intervalle de temps, mais en choisissant une direction aléatoire. Même si un tel mouvement ne correspond pas nécessairement à la réalité, il permet de découvrir des caractéristiques importantes applicables à des systèmes réels comme la modélisation de marchés boursiers en mathématiques financières ou du déplacement de molécules. |
MACHE ALÉATOIRE À UNE DIMENSION |
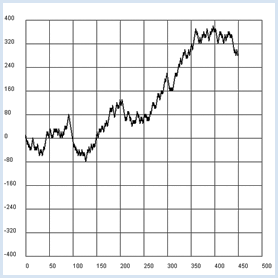
Une fois encore, les graphiques tortues sont très utiles pour représenter la simulation graphiquement. Au temps 0, la tortue se trouve à la position x = 0 et se déplace le long de l’axe Ox par pas d’égale longueur. À chaque pas, la tortue "décide" de faire un pas vers la gauche ou vers la droite de manière aléatoire. Dans le programme suivant, les deux choix surviennent avec la même probabilité p = ½ (marche aléatoire symétrique).
from gturtle import * from gpanel import * from random import randint makeTurtle() makeGPanel(-50, 550, -480, 480) windowPosition(880, 10) drawGrid(0, 500, -400, 400) title("Mean distance versus time") lineWidth(2) setTitle("Random Walk") t = 0 while t < 500: if randint(0, 1) == 1: setHeading(90) else: setHeading(-90) forward(10) x = getX() draw(t, x) t += 1 print("All done") |
MEMENTO |
Vous êtes peut-être surpris d’observer que, dans la plupart des cas, la tortue s’éloigne peu à peu de son point de départ alors même qu’elle fait, à chaque étape, un pas de même longueur à gauche ou à droite avec la même probabilité. Afin d’examiner ce résultat de manière plus minutieuse, notre prochain programme va déterminer la distance moyenne séparant la tortue du point de départ après t étapes parmi 1'000 marches aléatoires. |
LA LOI DE LA RACINE CARRÉE DU TEMPS |
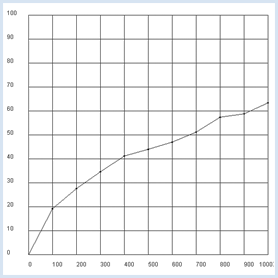
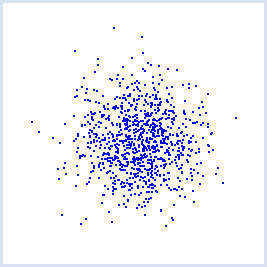
Le programme ci-dessous permet de visualiser de quelle distance une marche aléatoire de t pas s’éloigne de l’origine en moyenne pour t valant 100, 200, 300, …, 1000. Pour chaque nombre de pas t, la simulation est répétée 1000 fois (1000 marches aléatoires) dont le point d’arrivée est représenté à l’écran. La coordonnée y correspond au nombre de pas que comporte la marche aléatoire. Afin d’accélérer l’obtention des résultats, il est conseillé de cacher la tortue et d’éviter d’en dessiner la trace. Chacune de ces simulations permet de déterminer une distance r séparant le point final du point initial. Pour chaque jeu d’expériences avec un t donné, on obtiendra ainsi une distance d’éloignement moyenne avec le point de départ qui est reportée dans un graphique GPanel muni d’un repère orthonormé. from gturtle import * from gpanel import * from math import sqrt from random import randint makeTurtle() makeGPanel(-100, 1100, -10, 110) windowPosition(850, 10) drawGrid(0, 1000, 0, 100) title("Mean distance versus time") ht() pu() for t in range(100, 1100, 100): setY(250 - t / 2) label(str(t)) count = 0 repeat 1000: repeat t: if randint(0, 1) == 1: setHeading(90) else: setHeading(-90) forward(2.5) dot(3) r = abs(getX()) count += r setX(0) d = count / 1000 print("t =", t, "d =", d, "q = d / sqrt(t) =", d / sqrt(t)) draw(t, d) fillCircle(5) print("all done")
|
MEMENTO |
Comme la visualisation graphique le montre, la distance moyenne séparant le point d’arrivée du point de départ croît avec le nombre de pas de la marche aléatoire. Dans la console, on calcule également le quotient q = d / sqrt(t). Du fait qu’il est toujours pratiquement constant, on peut raisonnablement supposer que la relation d = q * sqrt(t) est vraie : La distance moyenne entre le point de départ et le point d’arrivée de la marche aléatoire augmente selon la racine carrée du temps (nombre d’étapes). |
LA MARCHE DU MEC BOURRÉ |
Les choses deviennent encore plus intéressantes lorsque la tortue peut se déplacer dans deux dimensions. Elle effectue alors une marche aléatoire à deux dimensions. La tortue effectue des pas de longueur identique mais dans des directions aléatoires.
from gturtle import * from gpanel import * from math import sqrt makeTurtle() makeGPanel(-100, 1100, -10, 110) windowPosition(850, 10) drawGrid(0, 1000, 0, 100) title("Mean distance versus time") ht() pu() for t in range(100, 1100, 100): count = 0 clean() repeat 1000: repeat t: fd(2.5) setRandomHeading() dot(3) r = math.sqrt(getX() * getX() + getY() * getY()) count += r home() d = count / 1000 print("t =", t, "d =", d, "q = d / sqrt(t) =", d / sqrt(t)) draw(t, d) fillCircle(5) delay(2000) print("all done") |
MEMENTO |
La loi de la racine carrée du temps s’applique également aux marches aléatoires à deux dimensions. En 1905, Albert Einstein en personne a démontré cette loi pour les particules de gaz dans son fameux article « Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen » qui fournit en passant une explication théorique au phénomène du mouvement Brownien. Une année plus tard, M. Smoluchowski est parvenu au même résultat en utilisant une idée différente. |
MOUVEMENT BROWNIEN |
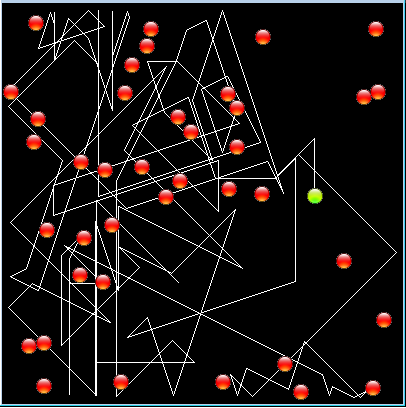
En 1827 déjà, le biologiste Robert Brown observa au microscope des grains de pollen en suspension dans une goutte d’eau effectuer des mouvements irréguliers de secousses. Il a interprété cette observation en attribuant une force vitale inhérente aux grains de pollen. Il a fallu attendre la découverte de la structure moléculaire de la matière pour pouvoir attribuer ce phénomène au mouvement thermique des molécules d’eau entrant en collision avec les grains de pollen. Le mouvement brownien peut être joliment montré dans une simulation informatique modélisant les molécules comme de petites sphères en mouvement qui échangent leur vitesse lors des collisions. Cette simulation peut être facilement implémentée à l’aide de JGameGrid puisqu’il est possible de gérer les collisions avec les événements. Pour ce faire, on crée une classe CollisionListener qui dérive de GGActorCollisionListener et on implémente le gestionnaire d’événements en redéfinissant la méthode collide(). On ajoute chaque particule à l’auditeur (listener en anglais) en utilisant addActorCollisionListener(). Il est possible de régler le type et la taille de la zone de collision à l’aide de la méthode setCollisionCircle(). Dans un souci de simplicité, les 40 particules sont réparties en quatre groupes de vitesses différents.
from gamegrid import * # =================== class Particle ==================== class Particle(Actor): def __init__(self): Actor.__init__(self, "sprites/ball.gif", 2) # Called when actor is added to gamegrid def reset(self): self.oldPt = self.gameGrid.toPoint(self.getLocationStart()) def advance(self, distance): pt = self.gameGrid.toPoint(self.getNextMoveLocation()) dir = self.getDirection() # Left/right wall if pt.x < 5 or pt.x > w - 5: self.setDirection(180 - dir) # Top/bottom wall if pt.y < 5 or pt.y > h - 5: self.setDirection(360 - dir) self.move(distance) def act(self): self.advance(3) if self.getIdVisible() == 1: pt = self.gameGrid.toPoint(self.getLocation()) self.getBackground().drawLine(self.oldPt.x, self.oldPt.y, pt.x, pt.y) self.oldPt.x = pt.x self.oldPt.y = pt.y # =================== class CollisionListener ========= class CollisionListener(GGActorCollisionListener): # Collision callback: just exchange direction and speed def collide(self, a, b): dir1 = a.getDirection() dir2 = b.getDirection() sd1 = a.getSlowDown() sd2 = b.getSlowDown() a.setDirection(dir2) a.setSlowDown(sd2) b.setDirection(dir1) b.setSlowDown(sd1) return 10 # Wait a moment until collision is rearmed # =================== Global section ==================== def init(): collisionListener = CollisionListener() for i in range(nbParticles): particles[i] = Particle() # Put them at random locations, but apart of each other ok = False while not ok: ok = True loc = getRandomLocation() for k in range(i): dx = particles[k].getLocation().x - loc.x dy = particles[k].getLocation().y - loc.y if dx * dx + dy * dy < 300: ok = False addActor(particles[i], loc, getRandomDirection()) # Select collision area particles[i].setCollisionCircle(Point(0, 0), 8) # Select collision listener particles[i].addActorCollisionListener(collisionListener) # Set speed in groups of 10 if i < 10: particles[i].setSlowDown(2) elif i < 20: particles[i].setSlowDown(3) elif i < 30: particles[i].setSlowDown(4) # Define collision partners for i in range(nbParticles): for k in range(i + 1, nbParticles): particles[i].addCollisionActor(particles[k]) particles[0].show(1) w = 400 h = 400 nbParticles = 40 particles = [0] * nbParticles makeGameGrid(w, h, 1, False) setSimulationPeriod(10) setTitle("Brownian Movement") show() init() doRun() |
MEMENTO |
Les molécules sont modélisées par la classe Particle dérivée de la classe Actor. Elles possèdent deux images de sprite, l’une rouge et l’autre verte, pour permettre de distinguer une molécule particulière dont on voudrait suivre le trajet. L’image verte correspond à spriteID = 1 qui est testé dans la méthode act() pour dessiner la trace avec drawLine(). |
EXERCICES |
|