8.1 SIMULATIONS
![]()
INTRODUCTION |
Les simulations par ordinateur ne jouent pas seulement un rôle important en recherche et dans l’industrie mais également dans le monde de la finance. Elles sont utilisées pour simuler le comportement d’un système réel complexe à l’aide d’un ordinateur. Comparées aux expériences et études réelles, les simulations informatiques présentent l’avantage d’être bon marché, écologiques et de ne présenter aucun danger. Elles ne peuvent cependant pas refléter parfaitement la réalité pour plusieurs raisons:
Il n’empêche que les simulations informatiques deviennent de plus en plus précises en raison de l’accroissement de la puissance de traitement des ordinateurs. Il suffit de penser aux prévisions météorologiques pour les prochains jours. Le hasard joue un rôle très important dans nos vies puisque nombre de nos décisions ne sont pas prises sur la base d’arguments purement logiques, mais suite à une estimation intuitive de valeurs probabilistes. Le recours au hasard peut également simplifier drastiquement des problèmes possédant une solution exacte. Il est par exemple extrêmement difficile et pratiquement impossible par un algorithme, en un temps raisonnable, le chemin le plus court entre deux villes A et B sur un réseau routier pourvu de nombreuses connexions [plus...On parle ici d’algorithmes stochastiques qui constituent actuellement un domaine de recherche de la plus haute importance]
|
L’ORDINATEUR COMME PARTENAIRE DE JEU |
Il est tout-à-fait possible de tester la validité de ce raisonnement en utilisant l’ordinateur et vos compétences de programmation. On suppose qu’il revient au même de lancer les trois dés en même temps ou l’un après l’autre. En d’autres termes, on suppose que les jets sont indépendants et que toutes les faces du dé surviennent de manière équiprobables avec probabilité 1/6. Il y a essentiellement deux manières d’attaquer ce problème : l’approche statistique et l’approche combinatoire. L’approche statistique correspond au jeu réel. On simule les jets de dés en générant de manière répétée trois nombres aléatoires compris entre 1et 6 et en dénombrant les cas gagnants. from random import randint n = 1000 # number of games won = 0 repeat n: a = randint(1, 6) b = randint(1, 6) c = randint(1, 6) if a == 6 or b == 6 or c == 6: won += 1 print("Won:", won, " of ", n, "games") print("My winning percentage:", won / n) Le résultat de la simulation indique que la probabilité d’un jeu gagnant vaut environ 0.42 et non 0.5 comme on s’y attendait. Cette valeur change bien entendu d’une simulation à l’autre car elle est sujette aux fluctuations statistiques. Comme on peut s’y attendre intuitivement, plus le nombre d’expériences est élevé, plus le résultat est précis. Les fluctuations statistiques jouent un rôle très important dans les simulations informatiques.
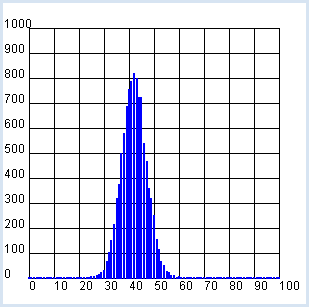
from gpanel import * from random import randint z = 10000 n = 100 def sim(): won = 0 repeat n: a = randint(1, 6) b = randint(1, 6) c = randint(1, 6) if a == 6 or b == 6 or c == 6: won += 1 return won makeGPanel(-10, 110, -100, 1100) drawGrid(0, 100, 0, 1000) h = [0] * (n + 1) title("Simulation started. Please wait...") repeat z: x = sim() h[x] += 1 title("Simulation ended") lineWidth(2) setColor("blue") for x in range(n + 1): line(x, 0, x, h[x])
|
MEMENTO |
|
Le maximum de la distribution se trouve environ à 42 puisque la probabilité de gagner vaut environ 0.42 et que l’on répète le jeu 100 fois. Si vous jouez 100 fois avec Nora, il est possible que vous gagniez plus de 50 fois, bien que la probabilité de gagner ne soit que de 0.42. La probabilité que cela arrive et cependant relativement faible (environ 5%) et le jeu est de ce fait inéquitable. Il faut toujours garder à l’esprit que les expériences par ordinateur impliquant des nombres aléatoires subissent des fluctuations statistiques qui s’atténuent lorsque l’on augmente le nombre d’essais. |
|
Quant à l’approche combinatoire, on laisse l’ordinateur tester toutes les possibilités de jeter trois dés l’un après l’autre. Le premier, le second et le troisième jet peuvent chacun résulter en un nombre compris entre un et six. On forme tous les triplets de nombres possibles dans la boucle imbriquée et l’on compte le nombre de possibilités totales dans la variable possible alors que l’on dénombre le nombre de cas gagnants dans la variable favorable. possible = 0 favorable = 0 for i in range(1, 7): for j in range(1, 7): for k in range(1, 7): possible += 1 if i == 6 or j == 6 or k == 6: favorable += 1 print("favorable:", favorable, "possible:", possible) print("My winning percentage:", favorable / possible) On voit que le nombre de cas favorables vaut 91 alors que le nombre de cas possibles vaut 216. Cela correspond à une probabilité de jeu gagnant de w = favorable / possible = 91/216 = 0.42, Valeur que nous avait déjà livré la simulation informatique.
MATÉRIEL SUPPLÉMENTAIREOn pourrait bien entendu résoudre ce problème sans utiliser l’ordinateur. Pour cela, on considère les trois événements gagnants E1, E2, E3:
Puisque E1, E2, et E3 sont indépendants les uns des autres, la probabilité d’un jeu gagnant vaut la somme des probabilités, à savoir 1/6 + 5/36 + 25/216 = 91/216 = 0.421296. On peut se représenter le processus dans un arbre:
Il existe encore une solution plus élégante qui consiste à calculer la probabilité de ne pas gagner, à savoir de n’obtenir aucun six du tout. Celle-ci vaut p = 5/6 * 5/6 * 5/6 = 125/216. De ce fait, la probabilité d’un jeu gagnant vaut w = 1 - p = 91/216. |
EXERCICES |
|