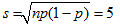8.3 HYPOTHÈSES ET TESTS STATISTIQUES
![]()
INTRODUCTION |
Dans un jeu consistant à tirer à pile ou face avec une pièce de monnaie, vous faites l’hypothèse (on l’appelle hypothèse nulle) que cette dernière est truquée, à savoir que les deux faces ne sont pas équiprobables. Vous utilisez un dé pour jouer et vous faites l’hypothèse qu’il n’est pas truqué, ce qui revient à dire que toutes ses faces apparaissent avec la même probabilité (p = 1/6). Dans ce chapitre, nous allons étudier une méthode permettant de tester ce genre d’hypothèses. Cela ne peut cependant pas se faire de manière absolument certaine puisque le principe consiste à rejeter l’hypothèse en limitant la probabilité de se tromper en la rejetant à 5% (risque de première espèce).
|
UNE PIÈCE SIGNIFICATIVEMENT BIAISÉE |
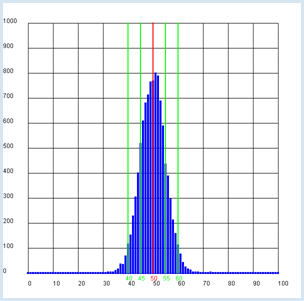
On pose l’hypothèse nulle que la pièce n’est pas biaisée et, en effectuant n = 100 jets, on obtient k fois pile et n-k fois face.
Le programme représente en plus le domaine de valeurs comprenant 95% de tous les résultats et met en évidence que cela correspond environ au double de la dispersion (ici entre 40 et 60). from gpanel import * from random import random n = 100 # size of the test group p = 0.5 z = 10000 def showDistribution(): setColor("blue") lineWidth(4) for t in range(n + 1): line(t, 0, t, h[t]) def showMean(): global mean count = 0 for t in range(n + 1): count += h[t] * t mean = int(count / z + 0.5) setColor("red") lineWidth(2) line(mean, 0, mean, 1000) text(mean - 1, -30, str(mean)) def showSpreading(level): count = h[mean] for s in range(1, 20): count += h[mean + s] + h[mean - s] if count > z * level: break setColor("green") lineWidth(2) line(mean + s, 0, mean + s, 1000) text(mean + s - 1, -30, str(mean + s)) line(mean - s, 0, mean - s, 1000) text(mean - s - 1, -30, str(mean - s)) def sim(): count = 0 repeat n: w = random() if w < p: count +=1 return count makeGPanel(-0.1 * n, 1.1 * n, -100, 1100) title("Coin toss, distribution of number") drawGrid(0, n, 0, 1000) h = [0] * (n + 1) repeat z: k = sim() h[k] += 1 showDistribution() showMean() showSpreading(0.68) showSpreading(0.95)
|
MEMENTO |
|
Si l’on répète un très grand nombre de fois l’expérience consistant à lancer une pièce de monnaie non biaisée 100 fois d’affilée, le nombre de jets « pile » obtenus sera compris dans l’intervalle [50-5, 50+5] dans 68 % des cas et dans l’intervalle [50-10, 50+10] dans 95% des cas [plus...
La valeur théorique calculée est Si l’on effectue un test avec une pièce de monnaie et que l’on obtient un nombre de jets « face » supérieur à 60 ou inférieur à 40, on rejette l’hypothèse que la pièce n’est pas biaisée. En d’autres termes, on admet que la pièce est biaisée. Dans ce cas, on pourrait rejeter l’hypothèse de manière erronée avec une probabilité de 5% (l’intervalle de confiance du test). Par souci de concision, on se contente parfois de dire que la pièce est significativement biaisée. |
UN DÉ SIGNIFICATIVEMENT BIAISÉ |
On considère un dé dont on veut tester s’il est non truqué, à savoir si toutes ses faces ont la même probabilité 1/6 de sortir. On pose l’hypothèse nulle que le dé n’est pas baisé. Il nous faudra dans cet exemple utiliser une méthode légèrement différente de celle vue pour la pièce de monnaie puisque chaque jet possède 6 issues possibles et non seulement deux, à savoir les entiers compris entre 1 et 6. Il est clair que pour obtenir un résultat significatif, il faudra lancer le dé un grand nombre de fois, disons 600 fois, et reporter les fréquences d’apparition des faces dans un tableau:
Fréquences observées et théoriques Pour introduire une mesure de l’écart entre les valeurs observées et les valeurs théoriques découlant de l’hypothèse que la pièce n’est pas biaisée, il faut calculer pour chaque face l’écart au carré relatif (u - e)2 / e et ajouter toutes ces valeurs. Ce résultat est appelé le χ2 (prononcer "khi-carré ").
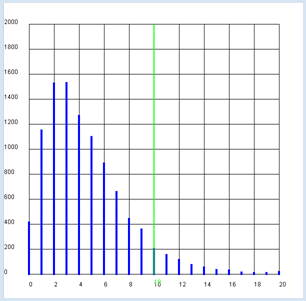
from gpanel import * from random import random, randint n = 600 # number of tosses p = 1 / 6 z = 10000 def showDistribution(): setColor("blue") lineWidth(4) for i in range(21): line(i, 0, i, h[i]) def showLimit(level): count = 0 for i in range(21): count += h[i] if count > z * level: break setColor("green") lineWidth(2) line(i, 0, i, 2000) text(i, -80, str(i)) return i def chisquare(u): chi = 0 e = n * p for i in range(1, 7): chi += ((u[i] - e) * (u[i] - e)) / e return chi def sim(): u = [0] * 7 repeat n: t = randint(1, 6) u[t] += 1 return chisquare(u) makeGPanel(-2, 22, -200, 2200) title("Chi-square simulation is being carried out. Please wait...") drawGrid(0, 20, 0, 2000) h = [0] * 21 repeat z: c = int(sim()) if c < 20: h[c] += 1 else: h[20] += 1 title("Chi-square test on the die") showDistribution() s = showLimit(0.95) # Observed series u1 = [0, 112, 128, 97, 103, 88, 72] u2 = [0, 112, 108, 97, 113, 88, 82] c1 = chisquare(u1) c2 = chisquare(u2) print("Die with", u1, "Xi-square:", c1, "loaded?", c1 > s) print("Die with", u2, "Xi-square:", c2, "loaded?", c2 > s)
|
MEMENTO |
|
La simulation informatique montre les résultats suivants : dans 95% des cas, χ2 st inférieur ou égal à la valeur critique 11 pour une pièce non biaisée. De ce fait, on a trouvé une méthode pour tester si un dé est pipé : il suffit de calculer le χ2des fréquences observées. Si la valeur obtenue est supérieure à 11, on peut affirmer avec une probabilité de se tromper de 5% que l’hypothèse nulle qu’il soit équilibré est fausse, et de ce fait, que le dé est pipé. Les fréquences issues du tableau ci-dessus donnent χ2 = 18.7. En d’autres termes, il y a une très forte probabilité que le dé en question soit pipé. Si, en faisant la même expérience avec un autre dé, on obtient les fréquences empiriques u2 = [112, 108, 97, 113, 88, 82] et vu que dans ce cas, χ2 = 8.5, il y a une faible probabilité que le dé en question soit pipé. |
DIFFÉRENCES DE COMPOREMENT CHEZ L’HUMAIN |
On peut également appliquer le test du χ2 l’étude du comportement de deux populations humaines. Une question intéressante qui survient souvent est de savoir si, dans un contexte particulier, le comportement des femmes et des hommes est statistiquement différent ou si les deux sexes se comportent de manière identique. Imaginons que l’on veuille faire une étude sur l’utilisation de Facebook dans une école secondaire. On demande à 106 filles et 86 garçons de cette école s’ils possèdent un compte Facebook. Le résultat de l’enquête sont les suivants:
On remarque que le pourcentage de personnes qui ont un compte Facebook est nettement plus grand chez les femmes que chez les hommes. Mais il faut encore s’assurer que cette probabilité plus élevée chez les femmes soit vraiment statistiquement significative.
Il faut encore déterminer la valeur attendue e pour chacun des quatre cas possibles. On suppose que la probabilité totale du "oui" est p = (f0 + m0) / n et, de manière correspondante, que 1-p est la probabilité totale du " Non". On calcule donc:
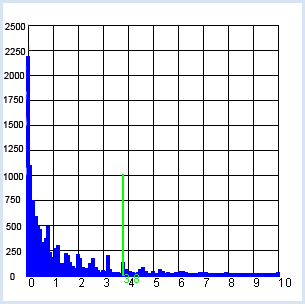
Le reste du programme demeure pratiquement inchangé par rapport au test avec le dé. from gpanel import * from random import random z = 10000 # survey values/polls females_yes = 87 females_no = 19 males_yes = 62 males_no = 24 def showDistribution(): setColor("blue") lineWidth(4) for i in range(101): line(i/10, 0, i/10, h[i]) def showLimit(level): count = 0 for i in range(101): count += h[i] if count > level * z: break setColor("green") lineWidth(2) limit = i / 10 line(limit, 0, limit, 1000) text(limit, -80, str(limit)) return limit def chisquare(f0, f1, m0, m1): # f: females, m: males, 0:yes, 1:no w = (f0 + m0) / n # probability of a yes # expected value ef0 = (f0 + f1) * w # females-yes em0 = (m0 + m1) * w # males-yes ef1 = (f0 + f1) * (1 - w) # females-no em1 = (m0 + m1) * (1 - w) # males-no # add up deviations (u - e)*(u - e) / e chi = (f0 - ef0) * (f0 - ef0) / ef0 \ + (m0 - em0) * (m0 - em0) / em0 \ + (f1 - ef1) * (f1 - ef1) / ef1 \ + (m1 - em1) * (m1 - em1) / em1 return chi def sim(): # simulate females f0 = 0 # yes f1 = 0 # no for i in range(females_all): t = random() if t < p: f0 += 1 else: f1 += 1 # simulate males m0 = 0 # yes m1 = 1 # no for i in range(males_all): t = random() if t < p: m0 += 1 else: m1 += 1 return chisquare(f0, f1, m0, m1) females_all = females_yes + females_no males_all = males_yes + males_no n = females_all + males_all # all p = (females_yes + males_yes) / n # probability of yes for all print("Facebook yes (all):", round(100 * p, 1), "%") pf = females_yes / females_all print("Facebook yes (females):", round(100 * pf, 1), "%") pm = males_yes / males_all print("Facebook yes (males:)", round(100 * pm, 1), "%") makeGPanel(-1, 11, -250, 2750) title("Chi-square test, use of Facebook") drawGrid(0, 10, 0, 2500) h = [0] * 101 repeat z: c = int(10 * sim()) # magnification factor of 10 if c < 100: h[c] += 1 else: h[100] += 1 showDistribution() s = showLimit(0.95) c = chisquare(females_yes, females_no, males_yes, males_no) print("critical value:", s) print("observed:", c) if c <= s: print("- the same behavior") else: print("- not the same behavior")
|
MEMENTO |
|
Le résultat est étonnant : le seuil de signification du χ2 se trouve autour des 3.8 [plus... Cette valeur correspond à ce que l’on trouve dans une table du χ2 à 1 degré de liberté et un seuil de signification de 95%]. Les résultats de l’enquête donnent un χ2 de 2.7. . On peut donc en conclure que, bien que la proportion de femmes inscrites sur Facebook soit bien plus élevée que pour les hommes, on ne peut pas prouver statistiquement à partir de cette enquête que leur comportement sur Facebook est significativement différent de celui des hommes. |
EXERCICES |
|