INTRODUCTION

If you want to investigate which problems a computer can generally solve, you first have to define what exactly a computing machine is. The famous mathematician and computer scientist Alan Turing published a study on this subject in 1936, long before a programmable digital computer even existed. The Turing machine, which was named after him, gradually runs programmatically through individual states. It does this on the basis of input values that it reads from a tape, and again writes output values onto the tape. This basic notion about how the computer functions are still valid today because each processor is actually a Turing machine that runs state by state at the ticks of a clock. However, state machines that can be modeled using transition graphs are better suited for practical applications. Because there is a finite number of states, they are called finite-state machines.

THE ESPRESSO MACHINE AS A MEALY MACHINE

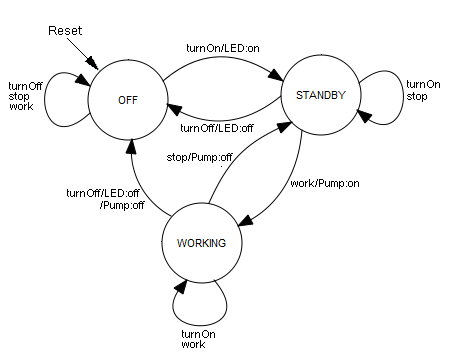
You are bound to encounter many devices and machines that you can regard as automata every single day. Automata include devices such as vending machines, washing machines, ATMs, and many others. As an engineer and computer scientist you develop such machines with the clear understanding that these perform their task in such way that they move from the current state to a successor state, depending on the sensor data and the operation of the buttons and switches. You call these the inputs of the automaton. Depending on the input values, the automaton operates certain actuators at each transition, such as motors, pumps, lights, etc. These are the outputs of the automaton.

In this example, you will develop an espresso machine that has 3 states: It can be turned off (OFF), it can be enabled and ready for operation (STANDBY) and it can be actively pumping water to make an espresso (WORKING). There are 4 push buttons available that allow you to operate the machine: turnOn, turnOff, work, and stop.

Although you can describe the operation of an espresso machine in words, it becomes much clearer if you draw an transition graph. For this, you illustrate the states as circles and the transitions as arrows that you can denote with the inputs/outputs. It is also important to determine which initial state the automaton is in when you connect it to the power line. Since any key can be pressed in each state, all inputs have to be possible at every state. If no action is performed, the output is omitted.

You can also record the behavior in a table in which you specify for each state s and each input t the successor state s'. You denote the initial state with a star.

Transition table:

In mathematical terms, you can say that the successor state s' is a function of the current state s and the input t: s' = F(s, t). You call F the transitional function.

You can also record the outputs belonging to each state and input:

Output table:

Here too, you can say mathematically that the output g is a function of the current state s and the input t: g = G(s, t). G is called the output function.

MEMO

IMPLEMENTING THE ESPRESSO MACHINE WITH STRINGS

A key press should trigger the transition from one state to the next. The respective key, one of the 4 cursor keys, specifies the input value. The implementation is quite straightforward: The program waits on a key entry in an endless event loop with getEntry(). With the return value, the current state is changed according to the transition table and the outputs are given according to the output table.

from gconsole import *

def getEntry():
    keyCode = getKeyCodeWait()
    if keyCode == 38: # up  
        return "stop"
    if keyCode == 40: # down
        return "work"
    if keyCode == 37: # left
        return "turnOff"
    if keyCode == 39: # right
        return "turnOn"
    return ""
    
state = "OFF"  # Start state
makeConsole()
while True:
    gprintln("State: " + state)
    entry = getEntry()
    if entry == "turnOff":
       if state == "STANDBY":
            state = "OFF"
            gprintln("LED off")
       if state == "WORKING":
            state = "OFF"
            gprintln("LED and pump off")
    elif entry == "turnOn":
        if state == "OFF":
            state = "STANDBY"
            gprintln("LED enabled")
    elif entry == "stop":
        if state == "WORKING":
            state = "STANDBY"
            gprintln("Pumpe off")
    elif entry == "work":
        if state == "STANDBY":
            state = "WORKING"
            gprintln("Pumpe enabled")

MEMO

ENUMERATIONS AS STATE AND EVENT IDENTIFIERS

Since the automaton operates with certain states, input values, and output values, it makes sense to introduce a particular data structure for that. Many programming languages offer a specific data type for enumeration. Unfortunately this data type is missing in the standard syntax of Python, but it can be added in TigerJython using the additional keyword enum(). You should use strings when defining the enumeration values, however they must adhere to the variable naming convention.

from gconsole import *

def getEvent():
    keyCode = getKeyCodeWait()
    if keyCode == 38: # up  
        return Events.stop
    if keyCode == 40: # down
        return Events.work
    if keyCode == 37: # left
        return Events.turnOff
    if keyCode == 39: # right
        return Events.turnOn
    return None
    
State = enum("OFF", "STANDBY", "WORKING")
state = State.OFF
Events = enum("turnOn", "turnOff", "stop", "work")
makeConsole()
while True:
    gprintln("State: " + str(state))
    event = getEvent()
    if event == Events.turnOn:
        if state == State.OFF:
            state = State.STANDBY
    elif event == Events.turnOff:
            state = State.OFF
    elif event == Events.work:
        if state == State.STANDBY:
            state = State.WORKING
    elif event == Events.stop:
        if state == State.WORKING:
            state = State.STANDBY

MEMO

MOUSE-CONTROLLED IMPLEMENTATION OF ESPRESSO MACHINE

MEMO

THINKING IN STATES WITH GRAPHICAL USER INTERFACES

At first glance, Mealy machines appear to be a rather theoretical matter. This is not at all the case. Rather, you must always think in states with modern, event-driven programs with a graphical user interface. As an example, you write a turtle program controlled by 3 buttons: The start_button sets the turtle in motion, the stop_button stops the movement, and the quit_button ends the program. In order to correctly implement the program, you have to keep the transition graph in mind::

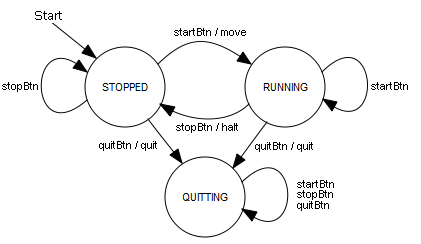
As you already know, no animations and only short-lasting code may be executed in GUI event callbacks, since the screen is only re-rendered at the end of the function. This is why in the callbacks of the button clicks you only modify the state, and you execute the movement of the turtle in the main part of the program.

(You can learn more about this problem in Appendix 4: Parallel processing)

from javax.swing import JButton
from gturtle import *

def buttonCallback(evt):
    global state
    source = evt.getSource()
    if source == runBtn:
        state = State.RUNNING
        setTitle("State: RUNNING")
    if source == stopBtn:
        state = State.STOPPED
        setTitle("State: STOPPED")
    if source == quitBtn:
        state = State.QUITTING
        setTitle("State: QUITTING")

State = enum("STOPPED", "RUNNING", "QUITTING")
state = State.STOPPED

runBtn = JButton("Run", actionPerformed = buttonCallback)
stopBtn = JButton("Stop", actionPerformed = buttonCallback)
quitBtn = JButton("Quit", actionPerformed = buttonCallback)
makeTurtle()
setTitle("State: STOPPED")
back(100)

pg = getPlayground()
pg.add(runBtn)
pg.add(stopBtn)
pg.add(quitBtn)
pg.validate()

while state != State.QUITTING and not isDisposed():
    if state == State.RUNNING:
          forward(200).left(127)
dispose()         

MEMO

EXERCISES

ADDITIONAL MATERIAL

ACCEPTORS FOR REGULAR LANGUAGES

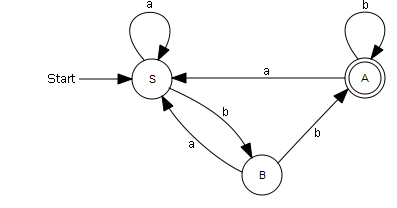
A formal language consists of an alphabet of symbols and a set of rules, which allows someone to clearly decide whether a particular sequence of symbols belongs to the language. If it is possible to implement the set of rules using an automaton, it is called a regular language.

In the implementation, the change of state is triggered by pressing the character keys a or b. Then, your program writes out the current state and the input word.

from gconsole import *

def getKeyEvent():
    global word
    keyCode = getKeyCodeWait(True)
    if keyCode == KeyEvent.VK_A:
        return Events.a
    if keyCode == KeyEvent.VK_B:
        return Events.b
    return None

State = enum("S", "A", "B")
state = State.S
Events = enum("a", "b")
makeConsole()
word = ""
gprintln("State: " + str(state))
while True:
    entry = getKeyEvent()
    if entry == Events.a:
        if state == State.A:
            state = State.S
        elif state == State.B:
            state = State.S
        word += "a"
        gprint("Word: " + word + " -> ")
        gprintln("State: " + str(state))
    elif entry == Events.b:
        if state == State.S:
            state = State.B
        elif state == State.B:
            state = State.A
        word += "b"
        gprint("Word: " + word + " -> ")
        gprintln("State: " + str(state))

MEMO

EXERCISES