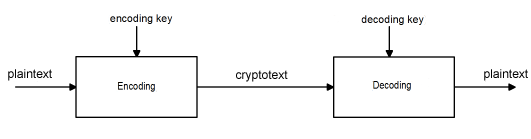
10.5 CRYPTOSYSTEMS
![]()
INTRODUCTION |
The principle of secrecy plays an increasingly important role in our modern world. To protect privacy, but to also maintain confidentiality of important government, industrial, and military information, it is necessary to encrypt data so that, if they fell into the hands of the wrong people, it would be impossible or at least very difficult to find out the original information without the disclosure of the decryption method.
|
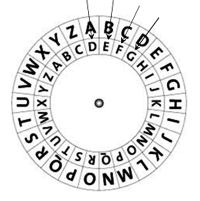
CAESAR CIPHER |
According to tradition, Julius Caesar (100 B.C. - 44 B.C.) already applied the following method for his military correspondence: Each plaintext letter is shifted down the alphabet to the right by a certain fixed number of places, continuing on to A again after Z.
The encoder encodes the read text string msg from the file using the function encode(msg), where each character is replaced by the corresponding crypto character, except for the line break \n. import string key = 4 alphabet = string.ascii_uppercase + " " def encode(text): enc = "" for ch in text: if ch != "\n": i = alphabet.index(ch) ch = alphabet[(i + key) % 27] enc += ch return enc fInp = open("original.txt") text = fInp.read() fInp.close() print("Original:\n", text) krypto = encode(text) print("Krypto:\n", krypto) fOut = open("secret.txt", "w") for ch in krypto: fOut.write(ch) fOut.close() Your encoded text reads as follows:
The decoder is built analogously, except that the characters in the alphabet are shifted backwards. import string key = 4 alphabet = string.ascii_uppercase + " " def decode(text): dec = "" for ch in text: if ch != "\n": i = alphabet.index(ch) ch = alphabet[(i - key) % 27] dec += ch return dec fInp = open("secret.txt") krypto = fInp.read() fInp.close() print("Krypto:\n", krypto) msg = decode(krypto) print("Message:\n", msg) fOut = open("message.txt", "w") for ch in msg: fOut.write(ch) fOut.close()
|
MEMO |
|
Keep in mind that you have to retain all empty spaces in the crypto text, even if they are at the beginning or the end of a line. It is clear that the encoding can be cracked easily. A good trick is to try it out for all key numbers 1 to 26. |
ENCODING WITH THE VIGENÈRE METHOD |
import string key = "ALICE" alphabet = string.ascii_uppercase + " " def encode(text): keyList = [] for ch in key: i = alphabet.index(ch) keyList.append(i) print("keyList:", keyList) enc = "" for n in range(len(text)): ch = text[n] if ch != "\n": i = alphabet.index(ch) k = n % len(key) ch = alphabet[(i + keyList[k]) % 27] enc += ch return enc fInp = open("original.txt") text = fInp.read() fInp.close() print("Original:\n", text) krypto = encode(text) print("Krypto:\n", krypto) fOut = open("secret.txt", "w") for ch in krypto: fOut.write(ch) fOut.close()
The decoder is again virtually identical. import string key = "ALICE" alphabet = string.ascii_uppercase + " " def decode(text): keyList = [] for ch in key: i = alphabet.index(ch) keyList.append(i) print("keyList:", keyList) enc = "" for n in range(len(text)): ch = text[n] if ch != "\n": i = alphabet.index(ch) k = n % len(key) ch = alphabet[(i - keyList[k]) % 27] enc += ch return enc fInp = open("secret.txt") krypto = fInp.read() fInp.close() print("Krypto:\n", krypto) msg = decode(krypto) print("Message:\n", msg) fOut = open("message.txt", "w") for ch in msg: fOut.write(ch) fOut.close()
|
MEMO |
|
The Vigenère encoding method was invented in the 16th century by Blaise de Vigenère and was considered very safe for centuries. If someone knows that the length of the keyword is 5, they must nevertheless try out 265 = 11'881'376 key numbers unless they know something about the word itself, for example that it is the first name of a woman. |
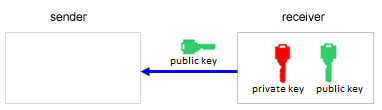
ENCODING WITH THE RSA METHOD |
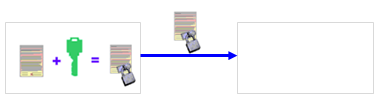
In this method, named after its inventors Rivest, Shamir and Adleman, a key-pair is used, namely a private key and a public key. The original data are encoded with the public key and decoded with the private key. It is an asymmetric cryptographic method.
The keys are generated using the following algorithm based on number theory [more... An elementary proof you can find in the book Barth, Algorithmics for beginners, Springer-Verlag]. First, two prime numbers p and q are chosen, which should have several hundred digits in order for the system to be secure. You multiply these and form m = p*q. From number theory, we know that the Euler function φ(m) = (p-1)*(q-1) is the total of co-prime numbers to m (a, b are co-prime if the largest common factor is ggT(a,b) = 1). Next, you select a number e that is smaller than φ and co-prime to φ. With this, we already have the public key and it consists of the number pair:
Below is an example with the small prime numbers p = 73 and q = 151: m = 73 * 151 = 11023, φ = 72 * 150 = 10800, e = 11 (chosen co-prime to φ)
The private key then consists of the number pair:
where for the number d we must ensure: (d * e) mod φ = 1 (since e and φ are co-prime, Bézout's lemma from number theory says that the equation has to have at least one solution). You can determine the number d with your values for e and φ using a simple program by trying out 100,000 values for d in a for loop. e = 11 phi = 10800 for d in range(100000): if (d * e) % phi == 1: print "d", d You get several solutions (5891, 16691, 27491, 49091, etc.). However, in principle you only need the first solution to determine the private key.
In this case, calculating the private key is only so easy because you already know the numbers p and q, and hence also the number φ. Without knowing these numbers, the private key can only be calculated with great effort. The RSA algorithm is used to encode numbers. In order to encode a text, you can use the ASCII code for each character and create the encoded value s with the public key [m, s] for the ciphertext according to the formula:
Write these encoded numbers line by line in the file secret.txt. publicKey = [11023, 11] def encode(text): m = publicKey[0] e = publicKey[1] enc = "" for ch in text: r = ord(ch) s = int(r**e % m) enc += str(s) + "\n" return enc fInp = open("original.txt") text = fInp.read() fInp.close() print("Original:\n", text) krypto = encode(text) print("Krypto:\n", krypto) fOut = open("secret.txt", "w") for ch in krypto: fOut.write(ch) fOut.close() In the decoder, you read the numbers from the file secret.txt (first) into a list. In order to decode, you calculate the original number according to the formula below which uses the private key s:
This is the ASCII code of the original character. privateKey = [11023, 5891] def decode(li): m = privateKey[0] d = privateKey[1] enc = "" for c in li: s = int(c) r = s**d % m enc += chr(r) return enc fInp = open("secret.txt") krypto = [] while True: line = fInp.readline().rstrip("\n") if line == "": break krypto.append(line) fInp.close() print("Krypto:\n", krypto) msg = decode(krypto) print("Message:\n", msg) fOut = open("message.txt", "w") for ch in msg: fOut.write(ch) fOut.close()
|
||||||||||
MEMO |
|
The big advantage of the RSA method is that no secret key information has to be exchanged between the sender and the receiver. Rather, the receiver generates both the public and the private key and only communicates the public key to the sender, while keeping the private key secret. The sender can now encode its data, but only the receiver can decode it [more... The transmitter and receiver can be connected also over an insecure channel, such as the Internet. ]. In practice, one could choose very large prime numbers p and q (several hundred digits longs). Generating the public key only requires the product formation m = p * q, which is very simple. If a hacker wants to find out the private key from the public key, they have to inversely determine both secret prime factors of m. Until now, factorizing a long number is only possible with an enormous amount of computational effort. That is how cryptosystems utilize the limits of calculability. In principle, however, there are no absolutely secure encoding methods. Encoding is already considered to be safe once the time it takes to decode is considerably longer than the time during which the information is of importance. |
EXERCISES |
|