deutsch     english    français     Print

 

8.7 COMPLEX NUMBERS & FRACTALS

 

 

INTRODUCTION

 

Complex numbers are very important in mathematics since they extend the set of real numbers allowing many propositions to be formulated easier and more general. They also play an important role in science and technology, especially in physics and electrical engineering [more... Quantum mechanics is based entirely on complex numbers and, in the field of electrical
engineering, the alternating current theory is greatly simplified by using complex numbers]. Fortunately, complex numbers are a built-in data type in Python and there are also arithmetic operators for addition, subtraction, multiplication, and division available for use. In addition, there are many known functions with complex arguments in the module cmath.

Complex numbers can be represented in the complex plane as arrows or as points. In order to allow that turtle windows, GPanels, and JGameGrid pixel grids can also be regarded as a complex planes, all functions with coordinate parameters (x,y) in the respective libraries are also directly available for complex numbers.

PROGRAMMING CONCEPTS: Complex data type, conformal mapping, Mandelbrot fractal

 

 

BASIC OPERATIONS WITH COMPLEX NUMBERS

 

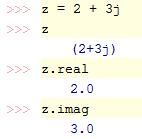
In Python, for the imaginary unit you use the symbol j commonly seen in electrical engineering instead of i. You can define the complex number with the real part 2 and the imaginary part 3 in several ways:

z = 2 + 3j   
or
z = 2 + 3 * 1j      
or
z  = complex(2, 3)

Use the convenient TigerJython console for the following examples:

You get the real and imaginary parts by using z.real and z.imag, respectively. You should keep in mind that these are not function calls but rather variable values (which you can only read). Real and imaginary parts are always floats.  
The square of the imaginary unit 1j is -1. In other words, the imaginary unit 1j is equal to the square root of -1. In order to get the square root of complex numbers, you have to import the module cmath instead of math  
The standard function abs() returns not only the value for integers and floats, but also for complex numbers. You can also use the usual operator symbols +, -, *, / and the power operator ** for complex numbers. They have the same order of precedence as for floats.  


In your program, you make powers of a complex number z = 0.9 + 0.3j, which has the absolute value of slightly less than 1. Since during the multiplication of two complex numbers the absolute values are multiplied and the phases added together , the powers seem to move on a spiral that you can easily draw in a GPanel. Remember that you have to do the filling before drawing the grid, because fill() always fills closed areas.

   



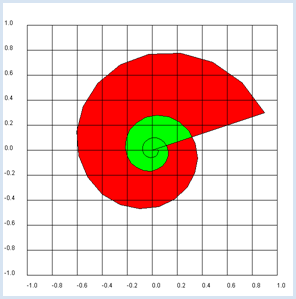
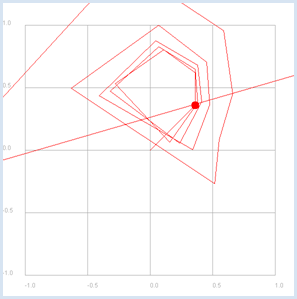
from gpanel import *
makeGPanel(-1.2, 1.2, -1.2, 1.2)
title("Complex plane")

z = 0.9 + 0.3j
for n in range(1, 60):
    y = z**n
    draw(y)
fill(0.2, 0, "white", "red")
fill(0.0, 0.2, "white", "green")
drawGrid(-1.0, 1.0, -1.0, 1.0)
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

draw(z) causes the same as draw(z.real, z.imag), but it is simpler. You should use GPanel coordinates that are 10% larger on all sides than the used coordinate range. You must specify the coordinates as floats in drawGrid() so that the grid is labeled with floats.

 

 

CONFORMAL MAPPING

 

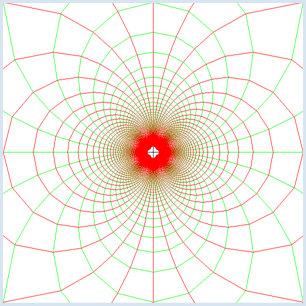
In a two-dimensional mapping every point P(x, y) is assigned a pixel P'(x', y').

You can also regard the points as complex numbers and say that the mapping of each number z is assigned a function value z'. Therefore, you write 
z' = f(z).


In the following, you choose the function z' = f(z) = 1/z (inversion) and map a perpendicular coordinate grid.

You select the area from -5 to 5 in the complex plane and conceive 201 grid lines with a spacing of 1/20. Draw the horizontal lines green and the vertical lines red. The result is a pretty picture

 

   


from gpanel import *

# function f(z) = 1/z
def f(z):
    if z == 0:
        return 0
    return 1 / z

min_value = -5.0
max_value = 5.0
step = 1 / 20
reStep = complex(step, 0)
imStep = complex(0, step)

makeGPanel(min_value, max_value, min_value, max_value)
title("Conformal mapping for f(z) = 1 / z")
line(min_value, 0, max_value, 0)  # Real axis
line(0, min_value, 0, max_value) # Imaginary axis

# Transform horizontal line per line
setColor("green")
z = complex(min_value, min_value)
while z.imag < max_value:
    z = complex(min_value, z.imag) # left
    move(f(z))
    while z.real < max_value: # move along horz. line
        draw(f(z))
        z = z + reStep
    z = z + imStep

# Transform vertical line per line
setColor("red")
z = complex(min_value, min_value)
while z.real < max_value:
    z = complex(z.real, min_value) # bottom
    move(f(z))
    while z.imag < max_value:  # move along vert. line
        draw(f(z))
        z = z + imStep
    z = z + reStep
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

What you can gather from the picture is that the images of the grid lines still intersect perpendicularly. A mapping where the angles between intersecting lines is maintained is called conformal and so we speak of a conformal mapping [more... It can be proved mathematically precise that the inversion is a conformal mapping] .

 

 

MANDELBROT FRACTALS

 


Many people are familiar with fractal images. It is likely that you have already encountered the Mandelbrot set, which you will program here yourself. The algorithm for many fractals is based on complex numbers, and because of this, it is very rewarding to work with them. The mathematician Benoit Mandelbrot is the father of fractal geometry (1924-2010).

   Mandelbrot at the introductory lecture of the Légion d'honneur (2006) (© Wiki)

To generate a Mandelbrot fractal you look at a (recursively defined) sequence of complex numbers for the given complex number c according to the formation rule

z'  =  z2  +  c     with the initial value     z0  =  0

If the amount of the sequence terms remains in a confined area, meaning that they do not grow beyond all limits, c belongs to the Mandelbrot set.

To familiarize yourself with the algorithm, you draw the following terms for two complex numbers
c1 = 0.35 + 0.35j and c2 = 0.36 +  0.36j. You will immediately see that c1 belongs to the Mandelbrot set, but c2 does not.



   

from gpanel import *

def f(z):
    return z * z + c

makeGPanel(-1.2, 1.2, -1.2, 1.2)
title("Mandelbrot iteration")

drawGrid(-1, 1.0, -1, 1.0, 4, 4, "gray")

isMandelbrot = askYesNo("c in Mandelbrot set?")
if isMandelbrot:
    c = 0.35 + 0.35j
    setColor("black")
else:
    c = 0.36+ 0.36j
    setColor("red")

title("Mandelbrot iteration with c = " + str(c))
move(c)
fillCircle(0.03)

z = 0j
while True:
    if z == 0:
        move(z)
    else:
        draw(z)
    z = f(z)
    delay(100)
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

To find out which numbers in a certain area of the complex plane belong to the Mandelbrot set, you execute the iteration for complex numbers c in a given range of the grid. Here you very simplistically assume that c does not belong to the Mandelbrot set if the absolute value of a sequence term in the first 50 iterations is greater than R = 2. If the absolute value of z remains less than 2 until the end of the 50 iterations, you assume that c belongs to the Mandelbrot set and you draw a black point there.

  

 


 
from gpanel import *

def isInSet(c):
    z = 0
    for n in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return False
    return True

maxIterations = 50
R = 2
xmin = -2
xmax = 1
xstep = 0.03
ymin = -1.5
ymax = 1.5
ystep = 0.03

makeGPanel(xmin, xmax, ymin, ymax)
line(xmin, 0, xmax, 0)  # real axis
line(0, ymin, 0, ymax) # imaginary axis
title("Mandelbrot set")
y = ymin
while y <= ymax:
    x = xmin
    while x <= xmax:
        c = x + y*1j
        inSet = isInSet(c)
        if inSet:
            move(c)
            fillCircle(0.01)
        x += xstep
    y += ystep
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

The Mandelbrot set is already visible in the graphic. You can draw figures that are even more beautiful if you draw a colored point for numbers c that do not belong to the Mandelbrot set, where the color says how quickly the sequence diverges. In this case, our measure of divergence is the number itCount, which represents the number of iterations after which the amount of z is greater than R = 2 for the first time.

To map itCount to a color, you can decide on any combination in getIterationColor() that in your opinion creates a particularly beautiful fractal.

 

 

  

 


 
from gpanel import *

def getIterationColor(it):
    color = makeColor((30 * it) % 256, 
                      (4 * it) % 256, 
                      (255 - (30 * it)) % 256)
    return color
    
def mandelbrot(c):
    z = 0
    for it in range(maxIterations):
        z = z*z + c
        if abs(z) > R: # diverging
            return it
    return maxIterations

maxIterations = 50
R = 2
xmin = -2
xmax = 1
xstep = 0.003
ymin = -1.5
ymax = 1.5
ystep = 0.003

makeGPanel(xmin, xmax, ymin, ymax)
title("Mandelbrot set")
enableRepaint(False)
y = ymin
while y <= ymax:
    x = xmin
    while x <= xmax:
        c = x + y*1j
        itCount = mandelbrot(c)
        if itCount == maxIterations: # inside Mandelbrot set
            setColor("black")
        else: # outside Mandelbrot set
           setColor(getIterationColor(itCount))
        point(c)
        x += xstep
    y += ystep
    repaint()
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

To speed up the drawing, you set enableRepaint(False) and only re-render at the end of each line using repaint().

The Mandelbrot fractal possesses the remarkable feature that when a section is magnified, a similar structure appears [more... However, the structure is not exactly the same and in this fractal is not strictly self-similarh] .

 

 

EXERCISES

 

1.


You can create a beautiful fractal if in a grid of the complex plane in the area between -20 and 20 you draw only the grid points z, for which the rounded absolute value is even, so int(abs(z) * abs(z)) % 2 == 0 applies. Choose an increment size of 0.1.
2.

Analyze the mappings of the complex plane:

a)   z' = f(z) = z2

b)   z' = f(z) = a * z   mit komplexem a = 2 + 1j

c)   z' = f(z) = ez

d) z' = f(z) = (1 - z)/ 1 + z (Möbius-Transformation)

Map a rectangular coordinate grid in the range between -5 and 5 with an increment value of 1/10. Describe the image with words and speculate on whether it is conformal.
3.

Draw some Mandelbrot fractals with different color mappings, for example:

 Number of iterations   Color
  < 3   dark gray
  < 5   green
  < 8   red
  < 10   blue
  < 100   yellow
  sonst   black

 

   

ADDITIONAL MATERIAL


 

ALTERNATING CURRENT AND IMPEDANCE

 

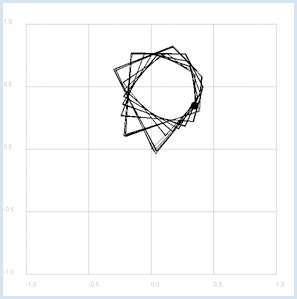
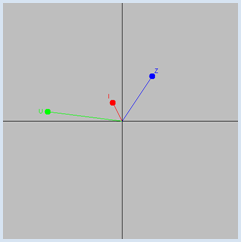
Electrical circuits for sinusoidal alternating voltages and alternating currents, which are built from passive devices (resistors, capacitors, inductors), can be treated like direct current circuits if you are using complex variables for voltages, currents, and resistors. A general complex resistor is also called an impedance and is often denoted with Z (and for purely imaginary resistors, X). The impedance of an ohmic resistor is R, of an inductor is XL = jωL (L: inductance) and of a capacitor is XC = 1 / jωC (C: capacitance), where ω = 2πf (f: frequency).

A complex alternating voltage u = u(t) runs uniformly on a circle in the complex plane. If it is applied to an impedance Z, the current i(t) flows according to Ohm's law u = Z * i. Since in complex multiplication the phases are added and the absolute values multiplied, u runs before i, phase-shifted by the phase of Z

phase(u) = phase(Z) + phase(i)

So, i also runs on a circle. The following absolute values (amplitudes) we have:

| u | = | Z | * | i |

In your program, you display these relationships in the complex plane with the values 

| u | = 5V and Z = 2 +3j

and a frequency of  f = 10 Hz. Since the graphic is completely erased, rebuilt, and rendered with repaint() in each step of the animation, use a GPanel with enableRepaint(False).

   


from gpanel import *
import math

def drawAxis():
   line(min, 0, max, 0)  # real axis
   line(0, min, 0, max) # imaginary axis


def cdraw(z, color, label):
    oldColor = setColor(color)
    line(0j, z)
    fillCircle(0.2)
    z1 = z + 0.5 * z / abs(z) - (0.1 + 0.2j)
    text(z1, label)
    setColor(oldColor)

min = -10
max = 10
dt = 0.001

makeGPanel(min, max, min, max)
enableRepaint(False)
bgColor("gray")
title("Complex voltages and currents")

f = 10 # Frequency
omega = 2 * math.pi * f

t = 0
uA = 5
Z = 2 + 3j

while True:
    u = uA * (math.cos(omega * t) + 1j * math.sin(omega * t))
    i = u / Z
    clear()
    drawAxis()
    cdraw(u, "green", "U")
    cdraw(i, "red", "I")
    cdraw(Z, "blue", "Z")
    repaint()
    t += dt
    delay(100)
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 
 

MEMO

 

Electrical circuits with passive devices can be treated as direct current circuits if you regard voltage, current, and resistance as complex numbers.

 
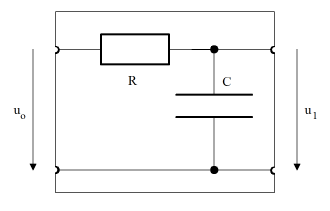
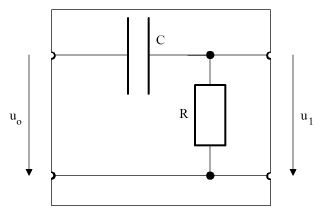
You can apply this knowledge to a simple circuit consisting of only a resistor and a capacitor. You are interested in finding the output voltage u1 dependent on the frequency f, regarding the input voltage uo, R and C as given.
  

The calculation is simple: The series circuit of R and C results in the impedance Z = R + XC and thus the current i = uo / Z, so again using Ohm's law the output voltage
  u1 = Xc * i = (  Xc  )/ R + Xc * u0 =  or   u1 = v * u0   with   v = (  Xc  )/ R + Xc  


v is called the complex amplification factor. You can visualize it in the complex plane for different values of f and you see that the amount of the value 1 decreases with increasing frequency at the frequency 0. Low frequencies are thus transferred well, whereas high frequencies are transferred poorly. This circuit would therefore be a low pass filter.

  


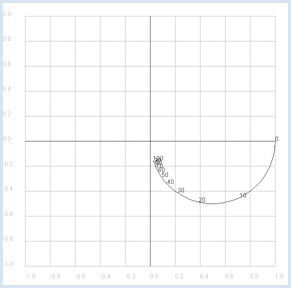
from gpanel import *
from math import pi

def drawAxis():
   line(-1, 0, 1, 0)  # Real axis
   line(0, -1, 0, 1) # Imaginary axis

makeGPanel(-1.2, 1.2, -1.2, 1.2)
drawGrid(-1.0, 1.0, -1.0, 1.0, "gray")
setColor("black")
drawAxis()
title("Complex gain factor – low pass")

R = 10
C = 0.001
def v(f):
    if f == 0:
        return 1 + 0j
    omega = 2 * pi * f
    XC = 1 / (1j * omega * C)
    return XC / (R + XC)

f = 0 # Frequency
while f <= 100:
    if f == 0:
        move(v(f))
    else:
        draw(v(f))
    if f % 10 == 0:
        text(str(f)) 
    f += 1
    delay(10)
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

The gain factor in the Bode plot is divided by magnitude and phase, and plotted in function of the frequency (logarithmic scales are commonly used).



   

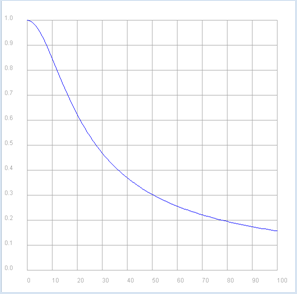
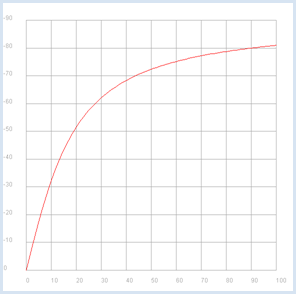
from gpanel import *
import math
import cmath

R = 10
C = 0.001

def v(f):
    if f == 0:
        return 1 + 0j
    omega = 2 * math.pi * f
    XC = 1 / (1j * omega * C)
    return XC / (R + XC)

p1 = GPanel(-10, 110, -0.1, 1.1)
drawPanelGrid(p1, 0, 100, 0, 1.0, "gray")
p1.title("Bode Plot - Low Pass, Gain")
p1.setColor("blue")
f = 0
while f <= 100:
    if f == 0:
        p1.move(f, abs(v(f)))
    else:
        p1.draw(f, abs(v(f)))
    f += 1

p2 = GPanel(-10, 110, 9, -99)
drawPanelGrid(p2, 0, 100, 0, -90, 10, 9, "gray")
p2.title("Bode Plot - Low Pass, Phase")
p2.setColor("red")
f = 0
while f <= 100:
    if f == 0:
        p2.move(f, math.degrees(cmath.phase(v(f))))
    else:
        p2.draw(f, math.degrees(cmath.phase(v(f))))
    f += 1
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

The Bode-Plot once again particularly clarifies that the present circuit transmits low frequencies well and high frequencies poorly. Additionally, a phase shift exists between the input and the output signal in the range of 0 to -90 degrees.

 

 

EXERCISES

 

1.


The frequency

  fc = (   1   )/ 2 π R C  

is called the cutoff frequency. Show that the amount of the gain factor for the RC low pass filter when R = 10 Ohm and C = 0.001 F at this frequency is:
 

2.

The amount of the gain factor is often specified in decibels (dB). It is defined dB = 20 log |v| (decimal logarithm). Draw the Bode diagram for the RC low pass filter with R = 10 Ohm and C = 0.001 F with a dB scale up to -100 dB and a logarithmic frequency scale in the range 1Hz..100 kHz.

Confirm that the roll-off for higher frequencies is 20 dB/(frequency decade) using the graphic illustration.
3.

The following circuit is a high pass filter (R = 10 Ohm, C = 0.001 F).

As you did in exercise 2, draw the Bode plot for the gain factor and discuss the frequency behavior.