deutsch     english    français     Print

 

8.2 POPULATIONS

 

 

INTRODUCTION

 

Computer simulations are often used to make predictions about the behavior of a system in the future, based on time observation or a certain time span in the recent past. Such predictions can be of great strategic significance and can prompt us, for example, to rethink early enough in a scenario leading to a catastrophe. Hot topics today are the prediction of the global climate and population growth.

We understand a population as a system of individuals whose number changes as a result of internal mechanisms, interactions, and external influences over the course of time. If external influences are disregarded, we speak of a closed system. For many populations the change in population size is proportional to the current size of the population. The change of the current value is calculated from the growth rate as follows:

   new value - old value = old value * growth rate * time interval

Because the left shows the difference of the new value from the old value, this relationship is called a difference equation. The growth rate can also be interpreted as an increase probability per individual and time unit. If it is negative, it decreases the size of the population. The growth rate may well change over the course of time.

PROGRAMMING CONCEPTS:
Difference equation, growth rate, exponential/limited growth, life table, population pyramid, predator-prey system

 

 

EXPONENTIAL GROWTH

 

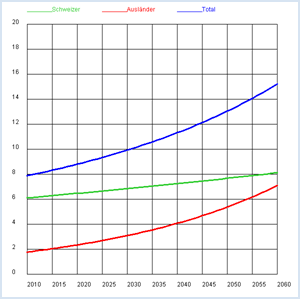
Population projections are of great interest and can massively affect the political decision-making process. The latest example is that of the debate going on about the regulation of the proportion of foreigners in the population.

You can find the number of inhabitants in Switzerland each year for the years 2010 and 2011 from the Swiss Federal Statistical Office (source:: http://www.bfs.admin.ch, keyword: STAT-TAB):

2010: Total z0 = 7 870 134, of which s0 =  6 103 857 are Swiss
2011: Total z1 = 7 954 662, of which s1 = 6 138 668 are Swiss

Can you create a forecast of the proportion of foreigners for the next 50 years from this information? You should first calculate the number of foreigners using the numbers a0 = z0 - s0 and a1 = z1 - s0 and from this the annual growth rate between 2010 and 2011 for Swiss and foreigners.

  rs =  (s1 - s0)/   s0 = 0.57%
bzw.
 ra =  (a1 - a0)/   a0 = 2.81%

It should now be easy for you to investigate the composition of the population for the next 50 years, provided that these growth rates remain the same. You can do this with a calculator, a spreadsheet program, or with Python. You can visualize the calculated values in a graph.

   


from gpanel import *

# source: Swiss Federal Statistical Office, STAT-TAB
z2010 = 7870134 # Total 2010
z2011 = 7954662 # Total 2011
s2010 = 6103857 # Swiss 2010
s2011 = 6138668 # Swiss 2011

def drawGrid():
    # Horizontal
    for i in range(11):
        y = 2000000 * i
        line(0, y, 50, y)
        text(-3, y, str(2 * i))
    # Vertical
    for k in range(11):
        x = 5 * k
        line(x, 0, x, 20000000)
        text(x, -1000000, str(int(x + 2010)))

def drawLegend():
    setColor("lime green")
    y = 21000000
    move(0, y)
    draw(5, y)
    text("Swiss")
    setColor("red")
    move(15, y)
    draw(20, y)
    text("foreigner")
    setColor("blue")
    move(30, y)
    draw(35, y)
    text("Total")
    
makeGPanel(-5, 55, -2000000, 22000000)
title("Population growth extended")
drawGrid()
drawLegend()

a2010 = z2010 - s2010 # foreigners 2010
a2011 = z2011 - s2011 # foreigners 2011

lineWidth(3)
setColor("blue")
line(0, z2010, 1, z2011)
setColor("lime green")
line(0, s2010, 1, s2011)
setColor("red")
line(0, a2010, 1, a2011)

rs = (s2011 - s2010) / s2010  # Swiss growth rate
ra = (a2011 - a2010) / a2010  # foreigners growth rate

# iteration
s = s2011
a = a2011
z = s + a
sOld = s
aOld = a
zOld = z
for i in range(0, 49):
    s = s + rs * s  # model assumptions
    a = a + ra * a  # model assumptions
    z = s + a
    setColor("blue")
    line(i + 1, zOld, i + 2, z)
    setColor("lime green")
    line(i + 1, sOld, i + 2, s)
    setColor("red")
    line(i + 1, aOld, i + 2, a)
    zOld = z
    sOld = s
    aOld = a
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

As you can gather from the figures, the proportion of foreigners doubles from 2010 to 2035, so just within 25 years, and in another 25 years it quadruples. With a the constant growth rate the population size obviously increases much faster than proportionally. If T is the doubling time, the population size y after time t for an initial size A is apparently:

y = A * 21/T

Since time is in the exponent, this rapid growth is called an exponential growth.

 

 

LIMITED GROWTH

 


Many populations reside in an environment with limited resources. The rapid exponential increase with a constant growth rate r is therefore bounded. Already about 100 years ago the biologist Carlson determined the following quantities (mg) for a yeast bacteria culture after each hour in an experiment:

 

  


1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
9.6 18.3 29.0 47.2 71.1 119.1 174.6 257.3 350.7 441.0 513.3 559.7 594.8 629.4 640.8 651.1 655.9 659.8 661.8

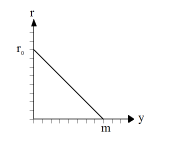
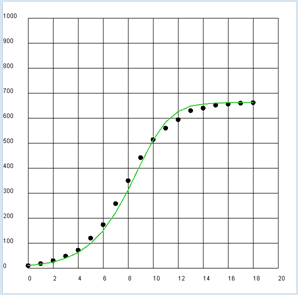
You can understand the experimental process with a model where the exponential growth experiences saturation. For this you can let the growth rate decrease linearly with an increasing population size y until it is zero at a certain saturation value m.

 

As you can easily verify by substituting y = 0 and y = m, we get the following formula:

r = r0 * (1 - (y)/ m ) = (r0)/ m * ( m - y)  

With this assumption, you can graphically display the temporal process and also draw the experimental values in a short program. To do this, repeat the difference equation with:

dy: new value - old value
y: old value
dt: time increment
λ: growth rate

so you can write:

<
  dy = y * r * dt = y * r0 * (1 - (r0)/ m ) * dt  
 


Using the initial value y0 = 9.6 mg, the saturation quantity m = 662 mg and the initial growth rate r0 = 0.62 /h we obtain a good correlation between theory and experiment.

from gpanel import *

z = [9.6, 18.3, 29.0, 47.2, 71.1, 119.1, 174.6, 257.3, 350.7, 441.0, 513.3, 
559.7, 594.8, 629.4, 640.8, 651.1, 655.9, 659.6, 661.8]

def r(y):
    return r0 * (1 - y / m)

r0 = 0.62
y = 9.6
m = 662

makeGPanel(-2, 22, -100, 1100)
title("Bacterial growth")
drawGrid(0, 20, 0, 1000)
lineWidth(2)
for n in range(0, 19):
    move(n, z[n])
    setColor("black")
    fillCircle(0.2)
    if n > 0:
        dy = y * r(y)
        yNew = y + dy
        setColor("lime green")
        line(n - 1, y, n, yNew)
        y = yNew
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

Assuming a linear decrease of the growth rate results in an “S” shaped saturation curve typical of the population size (also called logistic growth or sigmoid curve).

 

 

LIFE TABLES

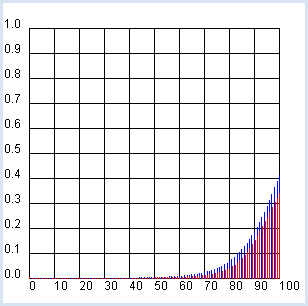
  A possible way to measure the health of a population is to look at the probability of surviving a certain age or of dying at an old age, respectively. If you wish to analyze the age distribution of the Swiss population, you can use current data from the Federal Statistical Office again, namely the so-called life tables (source: http://www.bfs.admin.ch, keyword: STAT-TAB). These tables contain the observed probabilities (qx and qy) for men and women to die at a certain age, separated by gender. Their determination is basically simple: one considers all deaths in the past year separately for men and women and calculates the frequency of 0-year-olds (people who died between birth and one year of age), 1-year-olds, etc. Afterwards, one divides each number by the total number in the corresponding age group at the beginning of the year.


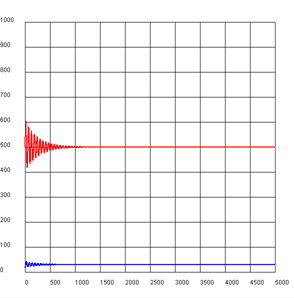
(You can create an Excel table for STAT-TAB and copy the columns for qx and qy into text files qx.dat or qy.dat, or just download the files from here. Copy them into the directory where your program is located.) Input the data into the program in a list qx or qy. Since the numbers sometimes contain spaces or apostrophes for better readability, you must remove them. First, you simply create a graphical representation of the read data.

 

   


import exceptions
from gpanel import *

def readData(filename):
    table = []
    fData = open(filename)

    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

makeGPanel(-10, 110, -0.1, 1.1)
title("Mortality probability (blue -> male, red  -> female)")
drawGrid(0, 100, 0, 1.0)
qx = readData("qx.dat")
qy = readData("qy.dat")
for t in range(101):
    setColor("blue")
    p = qx[t]
    line(t, 0, t, p)
    setColor("red")
    q = qy[t]
    line(t + 0.2, 0, t + 0.2, q)
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 


The curve clearly shows that on average, women live longer than men. The course in the first 30 years of life is also interesting.

Significantly more boys than girls die in the first year of life, as well as during the ages from 15- to 30-years old. Come up with some of your own thoughts about this graph.		  

 

 

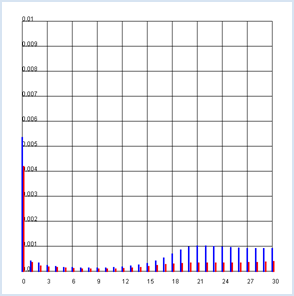
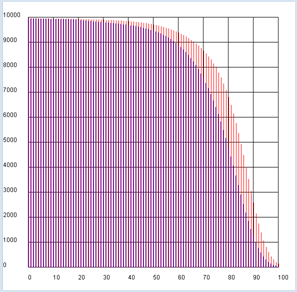
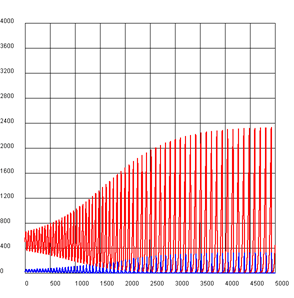
TEMPORAL EVOLUTION OF A POPULATION

 


With the help of the life table and a computer program, you can tackle many interesting demographic questions in a scientifically correct way. In this example you examine how a population of 10,000 newborns will evolve over the next 100 years. In doing so, use the values qx and qy as negative growth rates.

 

   


import exceptions
from gpanel import *

n = 10000 # size of the population

def readData(filename):
    table = []
    fData = open(filename)

    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

makeGPanel(-10, 110, -1000, 11000)
title("Population behavior/predictions  (blue -> male, red -> female)")
drawGrid(0, 100, 0, 10000)
qx = readData("qx.dat")
qy = readData("qy.dat")
x = n # males
y = n # females
for t in range(101):
    setColor("blue")
    rx = qx[t]
    x = x - x * rx
    line(t, 0, t, x)
    setColor("red")
    ry = qy[t]
    y = y - y * ry
    line(t + 0.2, 0, t + 0.2, y)
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

LIFE EXPECTANCY OF WOMEN AND MEN

 

In the previous analysis it became clear once again that women live longer than men. You can also express this difference with a single quantity called the life expectancy. This is the average achieved age of either women or men.

Briefly recall how an average, for example the average grade of a school class, is defined: You calculate the sum s of the grades of all students and divide it by the number of students n. If you are looking for simplicity, you can assume that only the integer grades between 1-6 occur and so you can calculate s as follows:

s = number of students with the grade 1 * 1 + number of students with the grade 2 * 2 + ... number of students with the grade 6 * 6

or more generally:

average = sum of (frequency of the value * value) divided by the total number

If you read the frequencies from a frequency distribution h of the values x (in this case, the grades 1 to 6), one also calls the average the expected value and you can write

  E = (x1 * h1 + x2 * h2+ ... + xn * hn)/         h1 + h2 + ... + hn

As you can see, the frequencie hi are weighted with their value xi in the sum.

Life expectancy is nothing else than the expected value for the age at which women and men die. In order to calculate it with a computer simulation, you begin with a certain amount of men and women (n = 10000) and determine the number of men (hx) or women (hy) that die between the ages t and t + 1. Evidently these numbers can be expressed as follows, using the size of the population x and y at the time t which you calculated in the previous program and the death rates rx and ry:

hx = x * rx  bzw. hy = y * ry

 

n = 10000 # size of the population

def readData(filename):
    table = []
    fData = open(filename)

    while True:
        line = fData.readline().replace(" ", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

qx = readData("qx.dat")
qy = readData("qy.dat")
x = n
y = n
xSum = 0
ySum = 0
for t in range(101):
    rx = qx[t]
    x = x - x * rx
    mx = x * rx # male deaths
    xSum = xSum + mx * t # male sum
    ry = qy[t]
    y = y - y * ry
    my = y * ry # female deaths
    ySum = ySum + my * t # female sum

print "Male life expectancy:", xSum / 10000
print "Female life expectancy:", ySum / 10000
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

The data of the Swiss population yields a life expectancy of men of about 76 years of women about 81 years.

 

 

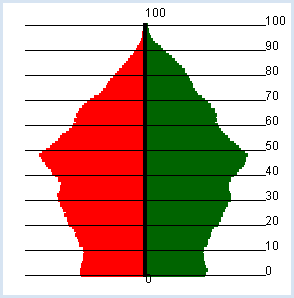
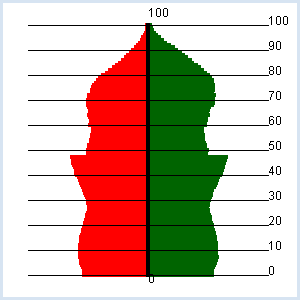
POPULATION PYRAMID

 

In demographic studies, the population is often grouped by year and from this, a frequency diagram is created. If you have two groups that you would like to compare, you can plot the frequencies of one group to the left and the ones of the other group to the right. Using this method for comparing women and men results in a beautiful pyramid-like graphic.

You can again take the current data (31. December 2012) from a table that you can find on the Swiss Federal Statistical Office website ( http://www.bfs.admin.ch, keyword: STAT-TAB) and copy them from the Excel table into the test files zx.dat and zy.dat. You can also download them hier.

 

   

import exceptions
from gpanel import *

def readData(filename):
    table = []
    fData = open(filename)
    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

def drawAxis():
    text(0, -3, "0")
    line(0, 0, 0, 100)
    text(0, 103, "100")

makeGPanel(-100000, 100000, -10, 110)
title("Population pyramid (green -> male, red ->  female)")
lineWidth(4)
zx = readData("zx.dat")
zy = readData("zy.dat")
for t in range(101):
    setColor("red")
    x = zx[t]
    line(0, t, -x, t)
    setColor("darkgreen")
    y = zy[t]
    line(0, t, y, t)
setColor("black")
drawAxis()
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

It is easy to spot the baby boomers born in the years 1955 – 1965 (47 - 57 years old).

 

 

CHANGE OF THE AGE DISTRIBUTION

 

An analysis of how the age distribution changes over decades can expose important information, such as how a society changes. You can simulate the current age distribution for the next 100 years under the following conditions:

  • There is no immigration or migration from the outside (closed society)
  • Deaths are taken into account according to the mortality tables
  • Each woman of childbearing age from 20 to 39 will have a certain number of children k (girls and boys are equally likely). At the moment we will assume k = 2.
  

With a key press you can show the following year.

import exceptions
from gpanel import *

k = 2.0

def readData(filename): 
    table = []
    fData = open(filename)
    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

def drawAxis():
    text(0, -3, "0")
    line(0, 0, 0, 100)
    text(0, 103, "100")
    lineWidth(1)
    for y in range(11):
        line(-80000, 10* y, 80000, 10 * y)
        text(str(10 * y))

def drawPyramid():
    clear()
    title("Number of children: " + str(k) + ", year: " + str(year) + 
          ", total population: " + str(getTotal()))
    lineWidth(4)
    for t in range(101):
        setColor("red")
        x = zx[t]
        line(0, t, -x, t)
        setColor("darkgreen")
        y = zy[t]
        line(0, t, y, t)
    setColor("black")
    drawAxis()
    repaint()

def getTotal():
    total = 0
    for t in range(101):
        total += zx[t] + zy[t]
    return int(total)

def updatePop():
    global zx, zy
    zxnew = [0] * 110
    zynew = [0] * 110
    # getting older and dying
    for t in range(101):
        zxnew[t + 1] = zx[t] - zx[t] * qx[t]    
        zynew[t + 1] = zy[t] - zy[t] * qy[t]
    # making a baby
    r = k / 20
    nbMother = 0
    for t in range(20, 40):
        nbMother += zy[t]
    zxnew[0] = r / 2 * nbMother
    zynew[0] = zxnew[0]
    zx = zxnew
    zy = zynew    

makeGPanel(-100000, 100000, -10, 110)
zx = readData("zx.dat")
zy = readData("zy.dat")
qx = readData("qx.dat")
qy = readData("qy.dat")
year = 2012
enableRepaint(False)
while True:
    drawPyramid()
    getKeyWait()
    year += 1
    updatePop()
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

It turns out that the future of the population is very sensitively dependent on the number k. Even with the value k = 2, the population decreases in the long term.

To stop the screen from flickering when you press a key, you should disable automatic rendering with enableRepaint(False). In drawPyramid() the graphics are then merely deleted from the backing storage (offscreen buffer), and are only newly rendered to the screen after the recalculation of repaint().

 

 

EXERCISES

 

1.


A population consists of 2 individuals at time 0. Each year it increases at a birth rate of 10% (number of births per year per individual). Simulate this for the first 100 years (display it graphically as a bar graph).
2a.

In a non-aging population, the mortality probability always remains the same regardless of age. There is no such population for living beings, but radioactive atoms (radionuclides) behave exactly this way. Instead of calling this mortality probability, we call it decay probability. Simulate a population of 10,000 radionuclides whose decay probability amounts to 0.1 for the first 100 years (display it graphically as a bar graph).

2b.

In the diagram, draw the times at which the population has shrunk to approximately 1/2, 1/4, 1/8, and 1/16 of the initial size, as vertical lines. What can you guess?
2c*

Radioactive decay takes place according to the following law:

N = N0 * e -λt

No: number of radionuclides at the time t = 0
N: number of radionuclides at the time t
λ: decay probability per time unit (decay constant)

Enter the best possible adapted curve shape using the color red in the graphic from 2a.
3.

Life expectancy can also be calculated by a statistical computer simulation. To do this, you simulate the life of a single individual from year to year. Let the computer choose a random number between 0 and 1 and allow the individual to die if the number is less than the mortality probability q. You then add up the achieved life duration. Once you have performed this simulation for 10,000 individuals, divide the total by 10,000. Determine the life expectancy of a female using this method with the values from qy.dat.

 

 

 

ADDITIONAL MATERIAL


 

PREDATOR-PREY SYSTEMS

 

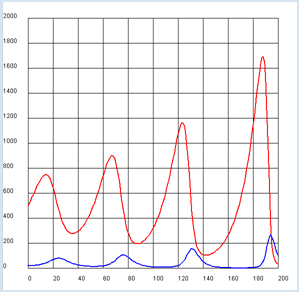
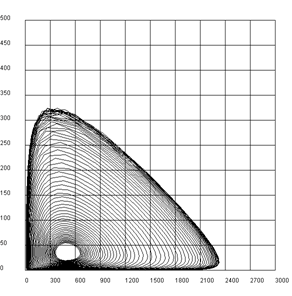
The behavior of two populations in a particular ecosystem which affect each other is very interesting. Assume the following scenario:
Bunnies and foxes reside in a closed territory. The bunnies multiply at a constant growth rate rx. If a fox meets a bunny, there is a certain probability that the fox will snatch it. In turn, the foxes die with a mortality rate ry. Their growth rate is determined by the consumption of bunnies.

If you assume that the probability of the foxes and bunnies meeting is equal to the product of the number of bunnies x and foxes y, there are two difference equations for x and y [more... These equations are the mathematical formulation of the Lotka-Volterra rules].

xNew - x = rx * x - gx * x * y
yNew - y = -ry * y + gy * x * y

Use the following values:

rx = 0.08
ry = 0.2
gx = 0.002
gy = 0.0004

and use the initial populations x = 500 bunnies and y = 20 foxes. For now, perform the simulation for 200 generations.

   


from gpanel import *

rx = 0.08
ry = 0.2
gx = 0.002
gy = 0.0004

def dx():
    return rx * x - gx * x * y

def dy():
    return -ry * y + gy * x * y
    
x = 500
y = 20

makeGPanel(-20, 220, -200, 2200)
title("Predator-Prey system (red: bunnies, blue: foxes)")
drawGrid(0, 200, 0, 2000)
lineWidth(2)
for n in range(200):
    xNew = x + dx()
    yNew = y + dy()
    setColor("red")
    line(n, x, n + 1, xNew)
    setColor("blue")
    line(n, y, n + 1, yNew)
    x = xNew
    y = yNew
Highlight program code (Ctrl+C to copy, Ctrl+V to paste)

 

 

MEMO

 

The number of the bunnies and foxes consistently fluctuates up and down. Qualitatively, this cycle is understood as follows: since the foxes eat the bunnies, they multiply particularly strongly, when there are many bunnies. Since this in turn depletes the population of the bunnies, the breeding of foxes slows down. It is during this time that the number of bunnies increases again (even beyond any limits).

 

 

EXERCISES

 

1.


Implement a boundary of the habitat for the bunnies according to the logistic growth with a growth rate rx' = rx(1 – x/m) with otherwise identical values as you did above. Show that when m = 2000 the oscillation decays over time, whereas when m = 3500 it oscillates regularly.

 
m = 2000, oscillation decays/fades away
  

m = 3500, oscillation is stable

2.

A chart/graph where the sizes of the population are plotted against each other is called a phase diagram. Write a program that draws the phase diagram for the two cases from exercise 1. Do you understand the behavior?