8.1 SIMULATIONS
![]()
INTRODUCTION |
Computer simulations do not only play an important role in research and in the industry, but also also in the finance world. They are used to simulate the behavior of a real system using a computer. Computer simulations have the advantage of being inexpensive and environmentally friendly, as well as safe, compared to real experiments and studies. However, they can usually never reflect reality with full accuracy. There are many reasons for this:
Nevertheless, computer simulations are becoming more and more precise with increasing computational power, just think of the weather forecasts for the next few days. Chance plays an exceptionally big role in our lives, as we make many decisions based on an intuitive assessment of probabilities and not just on the basis of purely logical arguments. However, the use of chance can also greatly simplify problems with exact solutions. One example is that it can be very time consuming to exactly determine the shortest possible path from A to B on a road map with many different connection possibilities using an algorithm; it is sufficient for practical use to find the most probably shortest possible path [more...These are randomized algorithms, a recent research area of great importance]PROGRAMMING CONCEPTS:
Computer simulation. computer experiment, statistical fluctuations |
THE COMPUTER AS A GAME PARTNER |
You can verify this thought process with the computer and your programming skills. You thereby assume that it does not matter whether you roll the 3 dice consecutively or all at the same time. So in other words, the probability of a die to obtain a certain number is independent of the other dice and it is always 1/6. from random import randint n = 1000 # number of games won = 0 repeat n: a = randint(1, 6) b = randint(1, 6) c = randint(1, 6) if a == 6 or b == 6 or c == 6: won += 1 print("Won:", won, " of ", n, "games") print("My winning percentage:", won / n) The result is a winning percentage of about 0.42, not 0.5 as you expected. The value easily changes from simulation to simulation though, because it is subject to statistical fluctuations. As you might intuitively expect, the result is more accurate the more tests you do. Statistical fluctuations are of great importance in computer simulations.
from gpanel import * from random import randint z = 10000 n = 100 def sim(): won = 0 repeat n: a = randint(1, 6) b = randint(1, 6) c = randint(1, 6) if a == 6 or b == 6 or c == 6: won += 1 return won makeGPanel(-10, 110, -100, 1100) drawGrid(0, 100, 0, 1000) h = [0] * (n + 1) title("Simulation started. Please wait...") repeat z: x = sim() h[x] += 1 title("Simulation ended") lineWidth(2) setColor("blue") for x in range(n + 1): line(x, 0, x, h[x])
|
MEMO |
|
The maximum of the distribution is approximately at 42, since the probability of winning is around 0.42 and you play 100 games each time. If you play 100 times with Nora it is possible that you win the game over 50 times, despite your only 0.42 chance of winning. However, the probability for this is quite low (ca. 5 %) and therefore the game is not fair. Computer experiments with random numbers are subject to statistical fluctuations that get smaller the larger number of attempts. |
|
For the combinatorial solution, you let the computer run all possible rolls with 3 dice one after another. The first, second, and third roll can each result in a number from 1 to 6. In the nested for loop you form all triples of numbers and count the total possibilities with the variable possible, whereas you count your winning cases which contain at least one 6 with the variable favorable. possible = 0 favorable = 0 for i in range(1, 7): for j in range(1, 7): for k in range(1, 7): possible += 1 if i == 6 or j == 6 or k == 6: favorable += 1 print("favorable:", favorable, "possible:", possible) print("My winning percentage:", favorable / possible) This results in 91 favorable of 216 possible cases and thus a winning probability w = favorable / possible of 91/216 = 0.42, which you also get with the computer simulation.
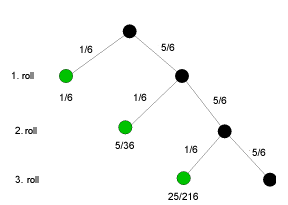
ADDITIONAL MATERIALYou could, of course, also solve this problem entirely without a computer. For this, think of the following: There are three possible winning events E1, E2, E3:
Since E1, E2, and E3 are independent of each other, the probability is the sum, i.e. 1 /6 + 5 /36 + 25 /216 = 91/216 = 0.421296. You can display the process as a tree:
There is also an ideal way to get the solution: the probability of rolling no 6's at all is p = 5/6 * 5/6 * 5/6 = 125/216. Therefore, the desired probability is w = 1 - p = 91/216. |
EXERCISES |
|