Recursions

deutsch english français Print

2.9 RECURSIONS

INTRODUCTION

Maybe you remember the slightly uncanny story of the man with the hollow tooth from your early childhood:

Äs isch ämal ä Ma gsi
dä het ä hohle Zahn gha
u i däm hohle Zahn isch äs Schachteli gsi
u i däm Schachteli isch äs Briefli gsi
u i däm Briefli isch gstande:
Äs isch ämal ä Ma gsi...

There once was a man
who had a hollow tooth
in this hollow tooth was a box
in the box was a letter
in the letter it said:
There once was a man...

Structures, which use themselves in their own definition, are called recursive. You likely already know the Russian Matryoshka dolls: One Matryoshka doll contains another slightly smaller Matryoshka doll inside of it, which contains another slightly smaller Matryoshka doll inside of it, which contains...

PROGRAMMING CONCEPTS: Recursion, recursion anchor, indirect recursion

RECURSIVE STAIRCASE

Suppose that you are asked to build a staircase with 3 steps. Instead of saying that you need to build a single step 3 separate times, you could also see a staircase with 3 steps as consisting of a step and a staircase with 2 steps. Then, a staircase with 2 steps is again composed of a step and a staircase with 1 step, which could again be seen as made of a single step and a staircase with 0 steps, which is of course nothing.

This construction manual is recursive, as in the definition of the staircase with 3 (or more generally n) steps, the staircase with 2 (or more generally n-1) stairs is used. Expressed in program code:

def stairs(n):
    step()
    stairs(n-1)

In a minute, you will instruct the turtle to draw a single step by defining the function step(). Then, you can simply call stairs(3) in order to build a stair with three steps. But wait, there is not yet an indication that nothing should happen when you build a staircase with 0 steps. You can easily solve this by using an if condition:

if n == 0:
   return

With the statement return, you tell the turtle to quit and return to its previous work. Your program should now look like this:

from gturtle import *

def stairs(n):
    if  n == 0:
        return
    step()
    stairs(n - 1)

def step():
    forward(50)
    right(90)
    forward(50)
    left(90)
    
makeTurtle()
fillToHorizontal(0)
stairs(3)

Highlight program code (Ctrl+C copy, Ctrl+V paste)

MEMO

Recursion is a fundamental solution method in the fields of mathematics and computer science, in which a problem is solved by turning it into the same but slightly simplified problem. Thus, if f is a function that solves the problem, in a (direct) recursion, f is used again in the definition of f [more... In a indirect recursion other functions that contain f used in the definition of f instead of f itself].

At first glance it may seem strange that someone would want to solve a problem in a way that already presupposes the solution. However, then we overlook an essential point: it is not the same problem that we use to find the solution, but one that is closer to the solution. In order to do this, we mostly use an integer parameter n, which we pass to f

def f(n):
   ...

The parameter is then reduced when f is called recursively:

def f(n):
   ...
   f(n-1)
   ...

A function defined this way would keep calling itself infinitely. To prevent this, you need a termination condition called a recursion anchor (or recursion base).

def f(n):
   if n == 0:
      return
   ...
   f(n - 1)
   ...

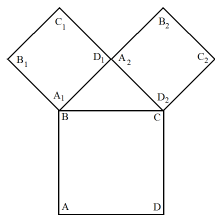
The further processing of the function is canceled using the keyword return. One also says that the function returns.

THE PYTHAGORAS TREE

You can create wonderful graphics with recursive algorithms. Try the following instructions:

	Begin at point A and draw a square ABCD making sure the base side is AD
	Add a right-angled isosceles triangle BD1C to the BC side of the square
	Draw the same again, taking A1D1 and A2D2 as the base sides of two new squares

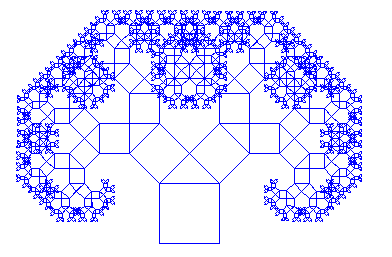
It is well-known that the implementation of a recursive program is unusual. Thus, the following will give you a detailed guide on how to proceed.

	Define a command square(s) with which the turtle can draw a square with the side length s and then return to the initial position where it again has the initial viewing direction.
	Define the command tree(s), where a tree is drawn, beginning with a square of side length s. In the definition you can reuse tree(). Important: After drawing the tree, the turtle must be back at the starting position having the original viewing direction. You should try to think about it as if you yourself were the turtle (the newly added code parts are highlighted in gray).

First draw a square with side length s starting at point A:

def tree(s):
     square(s)

Then go to the corner B of the square, turn 45 degrees to the left and look at this as a starting point for a new tree with a reduced parameter s1. Following the Pythagorean theorem, we obtain:

s₁ =

( s )/ √ 2

def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)   
   left(45)
   tree(s1)

Since you assumed that after drawing the tree you will be back at the starting point with the initial viewing direction, you find yourself back at point B and looking in the direction of B1.

Turn 90 degrees to the right and move forward by s1. Now you should be at the point D1, looking towards B2. From here you will draw the tree again.

def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)
   left(45)
   tree(s1)
   right(90)
   forward(s1)
   tree(s1)

Now you simply have to return to the initial point A with the original viewing direction. To do this, you need to move backwards by s1, turn 45 degrees to the left and then move backwards by s.

def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)
   left(45)
   tree(s1)
   right(90)
   forward(s1)
   tree(s1)
   back(s1)
   left(45)
   back(s)

from gturtle import *
import math

def tree(s):
    if s < 2:
        return
    square(s)
    forward(s)
    s1 = s / math.sqrt(2)
    left(45)
    tree(s1)
    right(90)
    forward(s1)
    tree(s1)
    back(s1)
    left(45)
    back(s)

def square(s):
    repeat 4:
        forward(s)
        right(90)

makeTurtle()
ht()
setPos(-50, -200)
tree(100)

Highlight program code (Ctrl+C copy, Ctrl+V paste)

MEMO

It is very important that the turtle returns back to its initial location with the initial viewing direction in many recursively defined figures.

EXERCISES

What is the essential difference between the two programs? Be sure to examine in particular the location and direction of the turtle after the program finishes. Why is figA called a "Last Line Recursion" and figB called a "First Line Recursion"?

from gturtle import *

def  figA(s):
   if s > 200:
      return
   forward(s)
   right(90)
   figA(s + 10)

makeTurtle()
figA(100)

from gturtle import *

def  figB(s):
   if s > 200:
      return
   figB(s + 10)
   forward(s)
   right(90)

makeTurtle()
figB(100)

The complete binary tree is a well-known graph. For a specific recursion depth, it looks as shown in the adjacent image. Write a recursive function tree(s) that draws a tree with "stem length" s.

Draw the adjacent star figure.
In order to do this, define the recursive function star(s) where the turtle can draw a star with the "dimension" s (s is the distance from the center of the star to the center of the figure in the next generation). s diminishes to 1/3 of the foregoing value. Call star(180) and anchor the recursion so that it breaks off at s < 20. If you use hideTurtle(), the turtle will draw much faster.

4*.

Now you will draw a tree that already almost looks like a real tree. Define the recursive function treeFractal(s) with the "stem length" s, which is constructed as follows:

	Anchor the recursion at a stem length less than 5
	First save the current x- and y-coordinates of the turtle with getX() and getY() as well as the viewing direction with heading(), so that you can easily return to the initial location
	Now move forward by s/3, turn 30 degrees to the left and draw the tree with the stem length 2*s/3
	Turn 30 degrees to the right, move forward by s/6, turn 25 degrees to the right and draw the tree with the stem length s/2
	Turn 25 degrees further to the right, move forward by s/3 and draw the tree with the stem length s/2 once again
	Return back to the initial location using setPos() and heading() with the save coordinates