2.9 RÉCURSIONS

 

 

INTRODUCTION

 

Vous vous rappelez peut-être de l’étrange histoire de l’homme à la dent creuse que l’on raconte volontiers aux petits enfants :

Äs isch ämal ä Ma gsi
dä het ä hohle Zahn gha
u i däm hohle Zahn isch äs Schachteli gsi
u i däm Schachteli isch äs Briefli gsi
u i däm Briefli isch gstande:
Äs isch ämal ä Ma gsi...		 Il était une fois un monsieur
qui avait une dent creuse
Dans cette dent creuse, était une boîte
dans la boîte, était une lettre
sur cette lettre, il était écrit:
Il était une fois un monsieur... .

 

  Des structures qui se font référence à elles-mêmes dans leur définition sont appelées récursives. Les poupées russes ou matryoshkas en sont un exemple très connu : une matryoshka contient une autre matryoshka légèrement différente et plus petite qui contient elle-même une autre matryoshka qui contient elle-même …
  CONCEPTS DE PROGRAMMATION: Récursion, ancrage de récursion, récursion indirecte

 

 

ESCALIERS RÉCURSIFS

  Admettons qu’il nous soit demandé de construire un escalier de trois marches. Au lieu de construire trois marches l’une après l’autre, on peut imaginer un escalier de trois marches comme une marche de longueur 3 surmontée d’un escalier de deux marches. Cet escalier de deux marches est alors constitué d’une marche de longueur 2 surmontée d’un escalier à une marche.

Cet escalier à une marche peut être lui-même considéré comme une marche de longueur 1 surmontée d’un escalier à zéro marche. Un escalier à zéro marche n’est composé de rien du tout et l’on peut s’arrêter de construire.

Cette procédure de construction est récursive puisque la définition d’un escalier de 3 marches (n marches de manière plus générale) repose sur un escalier de 2 marches (n-1 marches de manière plus générale). Sous forme de programme, cela donne:

def stairs(n):
    step()
    stairs(n-1)
 

Il ne reste plus qu’à instruire la tortue sur la façon de construire une marche de taille n en définissant la fonction step(). Il suffit ensuite d’appeler stairs(3) pour dessiner un escalier de trois marches. Notre programme ne fonctionnerait cependant pas en l’état, car il ne traite pas le cas de base d’un escalier à zéro marche. On peut facilement régler ce problème avec une condition if : 

if n == 0:
   return

L’instruction return interrompt l’exécution de la fonction, ce qui a pour effet d’interrompre le travail actuel et de retourner au travail en cours avant le dernier appel à step(). Voici à quoi devrait ressembler le programme après cet ajout indispensable:

from gturtle import *

def stairs(n):
    if  n == 0:
        return
    step()
    stairs(n - 1)

def step():
    forward(50)
    right(90)
    forward(50)
    left(90)
    
makeTurtle()
fillToHorizontal(0)
stairs(3)
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

La récursion est une méthode de résolution de problème essentielle en mathématiques et en informatique consistant à résoudre un problème en le transformant un en problème de même nature mais légèrement simplifié. Ainsi, dans une récursion directe, si f est une fonction qui qui fournit la solution cherchée, f est réutilisée dans sa propre définition [plus... Dans le cas d’une récursion indirecte, d’autres fonctions qui font appel à f sont utilisées pour définir la fonction f elle-même].

De prime abord, il peut paraître étrange de vouloir résoudre un problème par une méthode qui présuppose la connaissance de sa solution. Il faut noter cependant que la définition récursive ne présuppose pas la solution du même problème, mais d’un problème similaire de taille réduite, plus proche de la solution cherchée. Pour réduire la taille du problème, on définit la fonction récursive f avec un paramètre n 

def f(n):
   ...
Bei der Wiederverwendung von f im Definitionsteil wird der Parameter verkleinert:

def f(n):
   ...
   f(n-1)
   ...
Une fonction ainsi définie s’appellerait récursivement et n’aboutirait jamais à la solution cherchée. Pour éviter cela, il est nécessaire de définir un critère de terminaison appelé ancrage de la récursion.

def f(n):
   if n == 0:
      return
   ...
   f(n - 1)
   ...
L’instruction return prévient tout traitement ultérieur de la fonction.

 

 

L’ARBRE DE PYTHAGORE

 

Les algorithmes récursifs permettent de dessiner de magnifiques dessins. Voici comment obtenir l’arbre ci-dessus:

En partant du point A, dessiner un carré ABCD en s’assurant que sa base soit le côté AD
Ajouter un triangle rectangle isocèle BD1C au-dessus du côté BC du carré
Recommencer la procédure en prenant les cathètes du triangle rectangle isocèle comme bases des prochains carrés à dessiner
 

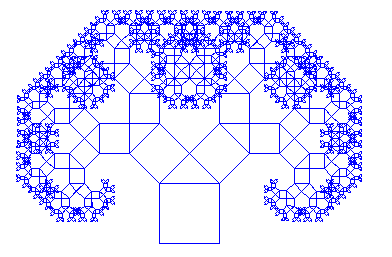
Il est bien établi que l’implémentation d’un programme récursif est inhabituelle. De ce fait, voici une procédure servant de guide dans l’élaboration de ce programme:

Définir une fonction square(s) qui ordonne à la tortue de dessiner un carré de côté s et qui s’assure qu’elle achève le dessin dans la même position et la même orientation qu’au début du dessin

Définir une fonction tree(s) permettant de dessiner un arbre en commençant par un carré dont la longueur du côté est s. Cette fonction peut s’appeler elle-même de manière récursive. Il est capital qu’après avoir dessiné l’arbre en question, la tortue se retrouve dans le même position et avec la même orientation que lorsqu’elle a débuté le dessin de cet arbre. Il est toujours judicieux dans ces cas de se mettre à la place de la tortue pour bien comprendre le programme. À chaque étape, les lignes ajoutées sont mises en évidence
On commence par dessiner le carré dont le côté mesure s en partant du point A 

 
def tree(s):
     square(s)
Ensuite, se rendre au point B, tourner de 45 degrés vers la gauche et considérer cette position et cette orientation comme le point de départ pour le dessin d’un prochain sous-arbre de longueur réduite s1. D’après le théorème de Pythagore, on a:
 
def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)   
   left(45)
   tree(s1)

Étant donné qu’après avoir dessiné un arbre, on se retrouve dans la position et l’orientation de départ, on se retrouve au point B avec une orientation de 45 degrés vers la gauche (Nord-Ouest) dans la direction du sommet B1

En se tournant de 90 degrés et en avançant d’une distance s1, la tortue se retrouve au point D1, orientée vers B2. Il s’agit de la condition initiale permettant de redessiner un arbre avec tree(s1)

 
def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)
   left(45)
   tree(s1)
   right(90)
   forward(s1)
   tree(s1)
Finalement, il est nécessaire de retourner au point initial A en adoptant l’orientation de départ. Pour ce faire, il suffit de reculer sur une distance s1, de tourner de 45 degrés vers la gauche et de reculer sur une distance s. 
def tree(s):
   square(s)
   forward(s)
   s1 = s / math.sqrt(2)
   left(45)
   tree(s1)
   right(90)
   forward(s1)
   tree(s1)
   back(s1)
   left(45)
   back(s)

from gturtle import *
import math

def tree(s):
    if s < 2:
        return
    square(s)
    forward(s)
    s1 = s / math.sqrt(2)
    left(45)
    tree(s1)
    right(90)
    forward(s1)
    tree(s1)
    back(s1)
    left(45)
    back(s)

def square(s):
    repeat 4:
        forward(s)
        right(90)

makeTurtle()
ht()
setPos(-50, -200)
tree(100)
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

Lorsqu’on dessine des motifs récursifs avec la tortue, il est très important qu’elle retrouve sa position et son orientation initiale après avoir effectué le dessin.

 

 

EXERCICES

 

1.


Expliquer la différence essentielle entre ces deux programmes. Examiner en particulier la position et l’orientation de la tortue à la fin du programme. Pourquoi figA est-elle appelée « Last Line Recursion » alors que figB est-elle appelée « First Line Recursion »? 


from gturtle import *

def  figA(s):
   if s > 200:
      return
   forward(s)
   right(90)
   figA(s + 10)

makeTurtle()
figA(100)

from gturtle import *

def  figB(s):
   if s > 200:
      return
   figB(s + 10)
   forward(s)
   right(90)

makeTurtle()
figB(100)

2.

L’arbre binaire complet est un graphe bien connu. La figure ci-contre représente un arbre binaire de profondeur 4. Le tronc unique est rajouté en plus et n’en fait pas partie à strictement parler. Définir une fonction récursive tree(s) qui dessine un arbre binaire complet (sans le tronc qu’il faut rajouter a posteriori) de taille s.

  


3.

Dessiner l’étoile ci-contre en définissant la fonction récursive star(s) où s représente la taille de l’étoile, à savoir la distance entre le centre de l’étoile et le centre des étoiles de la génération suivante. s diminue à 1/3 de sa valeur précédente. Dessiner l’étoile avec l’appel star(180) et définir l’ancrage de la récursion de telle sorte qu’elle s’arrête lorsque s < 20. En cachant la tortue avec hideTurtle(), le dessin se fera bien plus rapidement.
 

4*.


Maintenant, dessinez un arbre qui ressemble presque à un arbre réaliste. Dans ce but, définir une fonction treeFractal(s) dont la tige mesure s construit de la manière suivante:

Définir l’ancrage de la récursion de telle sorte qu’elle s’arrête lorsque la longueur s de la tige est inférieur à 5

Avant de commencer le dessin de l’arbre, sauver les coordonnées x et y avec les fonctions getX() et getY() ainsi que son orientation avec heading() de manière à pouvoir les restaurer facilement à la fin du dessin

Avancer de s / 3, tourner de 30 degrés vers la gauche et dessiner un arbre de taille 2*s/3

Tourner de 30 degrés vers la droite, avancer de s / 6, tourner de 25 degrés vers la droite et dessiner l’arbre de taille s/2

Tourner encore une fois de 25 degrés vers la droite, avancer de s / 3 et dessiner à nouveau un arbre de taille n / 2

Restaurer les coordonnées et l’orientation initiales avec les fonctions setPos(x, y) et heading(angle).