denkspiele

deutsch english français Imprimer

11.1 JEUX LOGIQUES AMUSANTS

INTRODUCTION

Les jeux logiques comportant un aspect mathématique sont très populaires et répandus. Le but de ce chapitre n’est pas de vous ôter le plaisir de résoudre ce genre de jeux à la main mais bien plutôt de mettre en évidence que l’ordinateur peut en trouver la solution de manière systématique à l’aide du retour sur trace (backtracking en anglais). Cela se fait néanmoins avec deux différences significatives. D’une part, en l’absence de stratégie particulière et de limite claire, l’exploration systématique par l’ordinateur peut prendre un temps colossal, même sur un ordinateur très puissant. D’autre part, l’ordinateur est capable de trouver toutes les solutions possibles, ce qui n’est souvent pas faisable à la main. Ceci permet d’exploiter l’ordinateur pour vérifier qu’une certaine solution est la meilleure et la plus courte.

SUDOKU

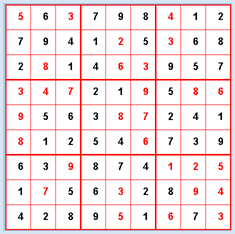
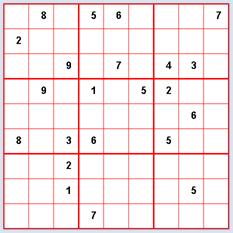
Le Sudoku a subi un gros boom depuis 1980 et n’a cessé de se répandre depuis pour devenir très populaire de nos jours et se retrouver dans pratiquement tous les quotidiens ou hebdomadaires. Il s’agit d’un jeu numérique dont les règles sont très simples. Dans la version standard, les nombres de 1 à 9 doivent être placés dans une grille 9x9 de sorte que chaque nombre n’apparaisse qu’une seule fois dans chaque ligne et chaque colonne. De plus, la grille est divisée en neuf sous-grilles de 3x3 cellules dans lesquels chaque nombre doit apparaître exactement une seule fois. La donnée du jeu consiste en une grille partiellement remplie. Idéalement, une grille initiale ne devrait comporter qu’une et une seule solution.

Selon la configuration initiale, le jeu peut être plus ou moins difficile à résoudre. Un joueur expérimenté use de certaines stratégies bien connues et d’autres plus personnelles pour trouver la solution. Dans l’algorithme du retour sur trace naïf effectué par l’ordinateur, aucune stratégie n’est mise en place: les cellules vides sont remplies une à une avec les nombres de 1 à 9 de telle sorte qu’il n’y ait pas de conflit selon les règles du jeu. Si l’algorithme se retrouve dans une impasse, le dernier essai est annulé.

Dans le programme suivant, l’ordinateur utilise le backtracking. La grille GameGrid est idéale pour la représentation graphique puisque le jeu a une structure de grille. On dessiner les nombres initiaux en noir comme des TextActor et on insère la solution en rouge.

Comme vous le savez à propos du backtracking depuis le chapitre 10.3., il faut d’abord trouver une structure de données appropriée pour stocker les états du jeu. Comme les états forment une grille 9x9, il faut choisir une liste composée de neufs listes représentant chacune une ligne. Le nombre 0 représente une cellule vide. De ce fait, la grille représentée ci-contre est représentée par l’état initial suivant:

startState = [ \
[0, 6, 0, 7, 9, 8, 0, 1, 2],
[7, 9, 4, 1, 0, 5, 0, 6, 8],
[2, 0, 1, 4, 0, 0, 9, 5, 7],
[0, 0, 0, 2, 1, 0, 5, 0, 0],
[0, 5, 6, 3, 0, 0, 2, 4, 1],
[0, 1, 2, 5, 4, 0, 7, 3, 9],
[6, 3, 0, 8, 7, 4, 0, 0, 0],
[1, 0, 5, 6, 0, 2, 8, 0, 0],
[4, 2, 8, 9, 0, 1, 0, 7, 0]]

Comme d’habitude, développons le programme étape après étape. La première tâche consiste à afficher un état donné dans la GameGrid et permettre à l’utilisateur de placer un nombre dans une cellule vide à l’aide de la souris. Bien que cette fonctionnalité ne soit pas nécessaire dans une résolution automatique du jeu, elle permet d’influencer le jeu de manière interactive, ce qui peut se révéler très utile dans la phase de test. Cela permet également de résoudre la grille à l’écran au lieu d’utiliser le papier et le crayon.

from gamegrid import *

def pressEvent(e):
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in fixedLocations:
        setStatusText("Location fixed")
        return
    x = loc.x
    y = loc.y
    value = startState[y][x]
    value = (value + 1)  % 10
    startState[y][x] = value
    showState(startState)
    
def showState(state):
    removeAllActors()
    for y in range(9):
        for x in range(9):
            loc = Location(x, y)
            value = state[y][x]
            if  value != 0:
                if loc in fixedLocations:
                    c = Color.black
                else:
                    c = Color.red
                digit = TextActor(str(value), c, Color.white, 
                        Font("Arial", Font.BOLD, 20))
                addActorNoRefresh(digit, loc)
    refresh()
    
makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent)
show()
setTitle("Sudoku")
setBgColor(Color.white)
getBg().setLineWidth(3)
getBg().setPaintColor(Color.red)
for x in range(4):
    getBg().drawLine(150 * x, 0, 150 * x, 450) 
for y in range(4):
    getBg().drawLine(0, 150 * y, 450, 150 * y) 

startState = [ 
[0, 6, 0, 7, 9, 8, 0, 1, 2],
[7, 9, 4, 1, 0, 5, 0, 6, 8],
[2, 0, 1, 4, 0, 0, 9, 5, 7],
[0, 0, 0, 2, 1, 0, 5, 0, 0],
[0, 5, 6, 3, 0, 0, 2, 4, 1],
[0, 1, 2, 5, 4, 0, 7, 3, 9],
[6, 3, 0, 8, 7, 4, 0, 0, 0],
[1, 0, 5, 6, 0, 2, 8, 0, 0],
[4, 2, 8, 9, 0, 1, 0, 7, 0]]
     
fixedLocations = [] 
for x in range(9):
    for y in range(9):
        if startState[y][x] != 0:
            fixedLocations.append(Location(x, y))

showState(startState)

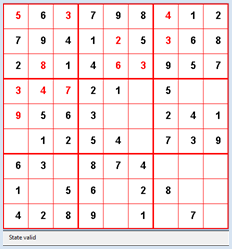
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

La prochaine étape consiste à définir une fonction isValid(state) qui vérifie qu’un état donné soit conforme aux règles du jeu. Il s’agit d’un travail fastidieux car il faut vérifier les 9 lignes, les 9 colonnes ainsi que les 9 sous-grilles 3x3. L’état de validité est affiché dans la barre d’état.

from gamegrid import *

def pressEvent(e):
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in fixedLocations:
        setStatusText("Location fixed")
        return
    xs = loc.x // 3
    ys = loc.y // 3
    x = loc.x % 3
    y = loc.y % 3
    value = startState[ys][xs][y][x]
    value = (value + 1)  % 10
    startState[ys][xs][y][x] = value
    showState(startState)
    if isValid(startState):
        setStatusText("State valid")
    else:
        setStatusText("Invalid state")

def showState(state):
    removeAllActors()
    for ys in range(3):
        for xs in range(3):
            for y in range(3):
                for x in range(3):
                    loc = Location(x + 3 * xs, y + 3 * ys)
                    value = state[ys][xs][y][x]
                    if  value != 0:
                        if loc in fixedLocations:
                            c = Color.black
                        else:
                            c = Color.red
                        digit = TextActor(str(value), c, Color.white, 
                                Font("Arial", Font.BOLD, 20))
                        addActorNoRefresh(digit, loc)
    refresh()

def isValid(state):
    # Check lines
    for ys in range(3):
        for y in range(3):
            line = []
            for xs in range(3):
                for x in range(3):
                    value = state[ys][xs][y][x]
                    if value > 0 and value in line:
                        return False
                    else:
                        line.append(value)    
    # Check rows
    for xs in range(3):
        for x in range(3):
            row = []
            for ys in range(3):
                for y in range(3):
                    value = state[ys][xs][y][x]
                    if value > 0 and value in row:
                        return False
                    else:
                        row.append(value)    

    # Check subgrids
    for ys in range(3):
        for xs in range(3):
            subgrid = state[ys][xs]
            square = []
            for y in range(3):
                for x in range(3):
                    value = subgrid[y][x]
                    if value > 0 and value in square:
                        return False
                    else:
                        square.append(value)
    return True

makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent)
show()
setTitle("Sudoku")
addStatusBar(30)
visited = []
setBgColor(Color.white)
getBg().setLineWidth(3)
getBg().setPaintColor(Color.red)
for x in range(4):
    getBg().drawLine(150 * x, 0, 150 * x, 450) 
for y in range(4):
    getBg().drawLine(0, 150 * y, 450, 150 * y) 

stateWiki = [[[[0, 3, 0], [0, 0, 0], [0, 0, 8]],
              [[0, 0, 0], [1, 9, 5], [0, 0, 0]],  
              [[0, 0, 0], [0, 0, 0], [0, 6, 0]]], 
             [[[8, 0, 0], [4, 0, 0], [0, 0, 0]],
              [[0, 6, 0], [8, 0, 0], [0, 2, 0]],
              [[0, 0, 0], [0, 0, 1], [0, 0, 0]]],
             [[[0, 6, 0], [0, 0, 0], [0, 0, 0]],
              [[0, 0, 0], [4, 1, 9], [0, 0, 0]],
              [[2, 8, 0], [0, 0, 5], [0, 7, 0]]]]   
startState = stateWiki

fixedLocations = [] 
for xs in range(3):
    for ys in range(3):
        for x in range(3):
            for y in range(3):
                if startState[ys][xs][y][x] != 0:
                    fixedLocations.append(Location(x + 3 * xs, y + 3 * ys))

showState(startState)

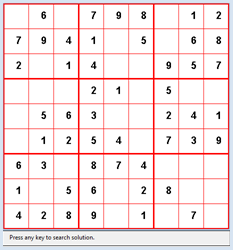
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

Pour effectuer le retour sur trace (backtracking), il est nécessaire de déterminer les sommets adjacents dans le graphe de transition des états du jeu avec la fonction getNeighbours(state). Pour ce faire, on choisit une cellule vide avec getEmptyCell() et on insère dans l’ordre tous les nombres appartenant à un état du jeu autorisé. Au moins l’un de ces nombres sera à coup sûr le bon.

Dans la fonction getNeighbours(state), on commence par cloner la grille partielle reçue en paramètre dans une deuxième liste clone à l’aide de cloneState(state). Cela est nécessaire pour pouvoir travailler sans danger dans cette grille puisqu’elle est passée par référence. Ne pas la cloner reviendrait à modifier la liste originale dans la partie appelante, ce qu’il faut à tout prix éviter dans ce cas (Voir la section « Modèle mémoire en Python » de ce même chapitre pour de plus amples explications à ce sujet). Ensuite, on choisit avec getEmptyCell(state) la prochaine cellule vide dans l’ordre de parcours de la grille choisi (en l’occurrence ligne après ligne, de haut en bas et de gauche à droite, selon la boucle imbriquée dans getEmptyCell). Chacun des neufs nouveaux états ainsi générés est ensuite cloné dans la liste d’états possibles validStates si isValid() indique qu’il est valide.

La fonction récursive search() qui effectue la recherche par backtracking peut être reprise pratiquement telle quelle des précédents problèmes résolus par backtracking puisque la partie dépendante du problème réside dans la fonction getNeighbours(state). Dans le cas présent, on ne cherche qu’une seule solution (les grilles de Sudoku bien formées ne possèdent qu’une solution) et on termine la récursion avec le fanion found puisqu’il est vain de poursuivre la recherche.

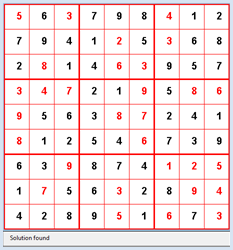
from gamegrid import *

def pressEvent(e):
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in fixedLocations:
        setStatusText("Location fixed")
        return
    x = loc.x
    y = loc.y
    value = startState[y][x]
    value = (value + 1)  % 10
    startState[y][x] = value
    showState(startState)
    if isValid(startState):
        setStatusText("State valid")
    else:
        setStatusText("Invalid state")

def getBlockValues(state, x, y):
    return [state[y][x], state[y][x + 1], state[y][x + 2], 
            state[y + 1][x], state[y + 1][x + 1], state[y + 1][x + 2],
            state[y + 2][x], state[y + 2][x + 1], state[ y + 2][x + 2]]
           
def showState(state):
    removeAllActors()
    for y in range(9):
        for x in range(9):
            loc = Location(x, y)
            value = state[y][x]
            if  value != 0:
                if loc in fixedLocations:
                    c = Color.black
                else:
                    c = Color.red
                digit = TextActor(str(value), c, Color.white, 
                        Font("Arial", Font.BOLD, 20))
                addActorNoRefresh(digit, loc)
    refresh()

def isValid(state):
    # Check lines
    for y in range(9):
        values = []
        for x in range(9):
            value = state[y][x]
            if value > 0 and value in values:
                return False
            else:
                values.append(value)    
    # Check rows
    for x in range(9):
        values = []
        for y in range(9):
            value = state[y][x]
            if value > 0 and value in values:
                return False
            else:
                values.append(value)    

    # Check blocks
    for yblock in range(3):
        for xblock in range(3):
            values = []
            li = getBlockValues(state, 3 * xblock, 3 * yblock)
            for value in li:
                if value > 0 and value in values:
                    return False
                else:
                    values.append(value)
    return True

def getEmptyCell(state):
    emptyCells = []
    for y in range(9):
        for x in range(9):
            if state[y][x] == 0:
                return [x, y]
    return []

def cloneState(state):
    li = []
    for y in range(9):
        line = []
        for x in range(9):
           line.append(state[y][x])
        li.append(line)
    return li
    
def getNeighbours(state):
    clone = cloneState(state)
    cell = getEmptyCell(state)
    validStates = []
    for value in range(1, 10):
        clone[cell[1]][cell[0]] = value
        if isValid(clone):
            validStates.append(cloneState(clone))
    return validStates

def search(state):
    global found, solution 
    if found:
        return
    visited.append(state)  # state marked as visited

    # Check for solution
    if getEmptyCell(state) == []:
        solution = state
        found = True
        return
        
    for neighbour in getNeighbours(state):
        if neighbour not in visited: # Check if already visited
            search(neighbour) # recursive call
    visited.pop() 
    
makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent)
show()
setTitle("Sudoku")
addStatusBar(30)
visited = []
setBgColor(Color.white)
getBg().setLineWidth(3)
getBg().setPaintColor(Color.red)
for x in range(4):
    getBg().drawLine(150 * x, 0, 150 * x, 450) 
for y in range(4):
    getBg().drawLine(0, 150 * y, 450, 150 * y) 

startState = [ 
[0, 6, 0, 7, 9, 8, 0, 1, 2],
[7, 9, 4, 1, 0, 5, 0, 6, 8],
[2, 0, 1, 4, 0, 0, 9, 5, 7],
[0, 0, 0, 2, 1, 0, 5, 0, 0],
[0, 5, 6, 3, 0, 0, 2, 4, 1],
[0, 1, 2, 5, 4, 0, 7, 3, 9],
[6, 3, 0, 8, 7, 4, 0, 0, 0],
[1, 0, 5, 6, 0, 2, 8, 0, 0],
[4, 2, 8, 9, 0, 1, 0, 7, 0]]

fixedLocations = [] 
for x in range(9):
    for y in range(9):
        if startState[y][x] != 0:
            fixedLocations.append(Location(x, y))

showState(startState)
setStatusText("Press any key to search solution.")
getKeyCodeWait(True)
setStatusText("Searching. Please wait...")
found = False
solution = None
search(startState)
if solution != None:
    showState(solution)
    setStatusText("Solution found")
else:
    setStatusText("No solution")

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

MEMENTO

Il est possible d’utiliser ce programme pour résoudre n’importe quel Sudoku publié sur le Web ou dans un journal. Avec suffisamment de patience, le programme finira toujours par trouver la solution.

On pourrait diminuer le temps de résolution en incluant les stratégies de résolution utilisées lors d’une résolution à la main. À vous d’améliorer l’algorithme de recherche en y incluant de telles heuristiques de recherche.

La méthode de résolution utilisée peut très bien servir également à résoudre des Sudokus dont les cellules ne sont pas carrées. Il suffit pour cela d’adapter la fonction getBlockValues() en conséquence.

LES VILAINS MARIS JALOUX

En 1613 déjà, le mathématicien C. G. Bachet, Sieur de Méziriac, publia une étude intitulée Problèmes plaisants et détectables qui se font par les nombres, dans laquelle il décrit le jeu logique nommé Les vilains maris jaloux dont voici la description :

"Trois maris jaloux se trouvent le soir avec leurs femmes au passage d'une rivière, et rencontrent un bateau sans batelier; le bateau est si petit, qu'il ne peut porter plus de deux personnes à la fois. On demande comment ces six personnes passeront de tel sorte qu'aucune femme ne demeure en la compagnie d'un ou de deux hommes, si son mari n'est présent, soit sur l'une des deux rives, soit sur le bateau." (Lit. Édouard Lucas, L'arithmétique amusante" 1885, reprint 2006)

Claude Gaspard Bachet de Méziriac (1581-1638) (© Wiki)

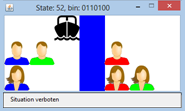
Pour résoudre ce problème, on procède à nouveau étape par étape. On commence par créer l’interface graphique (une grille GameGrid fera l’affaire) puisque les personnes impliquées peuvent facilement être représentées par des images de sprite. On ajoute les acteurs à une grille invisible 7x3, ce qui permet de dessiner une rivière sur la bande du milieu. Puisque la seule chose qui importe est de savoir si une personne donnée est à gauche ou à droite de la rivière, on choisit comme structure de données un nombre binaire dont chacun des bits représente l’état d’une personne bien précise. Un bit à 0 signifie que la personne est à gauche et un bit à 1 qu’elle est à droite de la rivière. On utilise le bit de poids fort (celui ayant la plus grande valeur) pour représenter la position du bateau.

Dans le programme de simulation, il y a un couple de chaque couleur (rouge, vert, bleu) ainsi que le bateau qui sont associés de la manière suivante aux bits d’état:

b6	b5	b4	b3	b2	b1	b0
bateau	H_rouge	F_rouge	H_vert	F_verte	H_bleu	F_bleue

où b0 est le bit de poids faible (ayant la plus faible valeur numérique). En interprétant l’état du jeu dans le système décimal, l’ensemble des nombres entre 0 et 127 représentent les 128 états possibles au niveau des positions.

Il est fortement recommandé d’interrompre la lecture pour se familiariser avec la représentation des états sous forme de nombres binaires à l’aide du programme de simulation. Il faut cliquer sur un personnage ou sur le bateau pour le faire passer de l’autre côté de la rivière. L’état binaire ainsi que sa valeur décimale sont alors affichés dans la barre d’état.

You already build a test here with isStateAllowed(state) to check if the current situation is legal according to the rules. (You could also first create a prototype without this test.)

from gamegrid import *

def pressEvent(e):
    global state
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in left_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    if loc in right_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    state = 0
    for i in range(7):
        loc = right_locations[i]
        actor = getOneActorAt(loc)
        if actor != None:
            state += 2**(6 - i)
    showState(state)

def stateToString(state):
    return str(bin(state)[2:]).zfill(7)

def showState(state):
    sbin = stateToString(state)
    for i in range(7):
        if sbin[i] == "0":
           actors[i].setLocation(left_locations[i])
        else:
           actors[i].setLocation(right_locations[i])
    setTitle("State: " + str(state) + ", bin: " + stateToString(state)) 
    if isStateAllowed(state):
        setStatusText("Situation allowed")
    else:
        setStatusText("Situation not allowed")
    refresh()

def isStateAllowed(state):
    print(state)
    stateStr = stateToString(state)
    mred = stateStr[1] == "1"
    fred = stateStr[2] == "1"
    mgreen = stateStr[3] == "1"
    fgreen = stateStr[4] == "1"
    mblue = stateStr[5] == "1"
    fblue = stateStr[6] == "1"

    if mred and not fred or not mred and fred: # mred/fred not together
        if not fred and (not mgreen or not mblue) or fred and (mgreen or mblue):
            return False
    if mgreen and not fgreen or not mgreen and fgreen:#mgreen/fgreen not together
        if not fgreen and (not mred or not mblue) or fgreen and (mred or mblue):
            return False
    if mblue and not fblue or not mblue and fblue:  # mblue/fblue not together
        if not fblue and (not mred or not mgreen) or fblue and (mred or mgreen):
            return False
    return True   

makeGameGrid(7, 3, 50, None, False, mousePressed = pressEvent)
setBgColor(Color.white)
addStatusBar(30)        
show()
actors = [Actor("sprites/boat.png"), 
   Actor("sprites/man_0.png"), Actor("sprites/woman_0.png"),
   Actor("sprites/man_1.png"), Actor("sprites/woman_1.png"),
   Actor("sprites/man_2.png"), Actor("sprites/woman_2.png")]

left_locations =  [Location(2, 0), 
                   Location(2, 1), Location(2, 2), 
                   Location(1, 1), Location(1, 2), 
                   Location(0, 1), Location(0, 2)] 
right_locations = [Location(4, 0), 
                   Location(4, 1), Location(4, 2), 
                   Location(5, 1), Location(5, 2), 
                   Location(6, 1), Location(6, 2)] 

for i in range(7):
    addActorNoRefresh(actors[i], left_locations[i])
for i in range(3):    
   getBg().fillCell(Location(3, i), Color.blue)   
refresh()

startState = 0
showState(startState)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

Dans une deuxième étape de développement, on implémente l’algorithme de recherche par backtracking bien connu du chapter 10.3. Encore une fois, il faut déterminer tous les états possibles atteignables à partir de l’état courant state au sein d’une fonction getNeighbours(state) qui fonctionne de la manière suivante

On commence par déterminer si le bateau se situe sur la rive gauche (state < 64) ou sur la rive droite (state >= 64).
On dresser dans li_one la liste de toutes les personnes qui sont en mesure de traverser la rivière en solo et dans li_two la liste des personnes pouvant traverser la rivière par équipes de deux.
Il faut encore s’assurer à l’aide de removeForbiddenTransfers() qu’aucun transfert déterminé aux étapes précédentes n’implique une épouse et un homme d’un autre couple.

La recherche par backtracking est implémentée de manière familière dans la fonction search(). On copie ensuite les solutions possibles dans une liste solutions qu’il sera possible d’examiner une fois le processus de recherche terminé. Ceci permet de compter le nombre de solutions possibles et de déterminer celle qui implique le moins de traversées et qui peut être visualisée pas à pas avec n’importe quelle touche du clavier.

from gamegrid import *
import itertools

def pressEvent(e): 
    global state
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in left_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    if loc in right_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    state = 0
    for i in range(7):
        loc = right_locations[i]
        actor = getOneActorAt(loc)
        if actor != None:
            state += 2**(6 - i)
    setTitle("State: " + str(state) + ", bin: " + stateToString(state)) 
    if isStateAllowed(state):
        setStatusText("Situation allowed")
    else:
        setStatusText("Situation not allowed")
    refresh()

def stateToString(state):
    return str(bin(state)[2:]).zfill(7)

def showState(state):
    sbin = stateToString(state)
    for i in range(7):
        if sbin[i] == "0":
           actors[i].setLocation(left_locations[i])
        else:
           actors[i].setLocation(right_locations[i])
    refresh()

def getTransferInfo(state1, state2):
    state1 = state1 & 63
    state2 = state2 & 63
    mod = state1 ^ state2
    passList = []
    for n in range(6):
        if mod % 2 == 1:
            if n // 2 == 0:
                couple = "blue"
            elif n // 2 == 1:
                couple = "green"
            elif n // 2 == 2:
                couple = "red"
            if n % 2 == 0:
               passList.append("f" + couple)
            else:
               passList.append("m" + couple)
        mod = mod // 2
    return passList

def getTransferSequence(solution):
    transferSequence = []
    oldState = solution[0]
    for state in solution[1:]:
        transferSequence.append(getTransferInfo(oldState, state))
        oldState = state
    return transferSequence

def isStateAllowed(state):
    stateStr = stateToString(state)
    mred = stateStr[1] == "1"
    fred = stateStr[2] == "1"
    mgreen = stateStr[3] == "1"
    fgreen = stateStr[4] == "1"
    mblue = stateStr[5] == "1"
    fblue = stateStr[6] == "1"

    if mred and not fred or not mred and fred:  # mred/fred not together
        if not fred and (not mgreen or not mblue) or fred and (mgreen or mblue):
            return False
    if mgreen and not fgreen or not mgreen and fgreen:#mgreen/fgreen not together
        if not fgreen and (not mred or not mblue) or fgreen and (mred or mblue):
            return False
    if mblue and not fblue or not mblue and fblue:  # mblue/fblue not together
        if not fblue and (not mred or not mgreen) or fblue and (mred or mgreen):
            return False
    return True

def removeForbiddenTransfers(li):
    forbiddenPairs = [(0, 3), (0, 5), (1, 2), (2, 5), (1, 4), (3, 4)]
    allowedPairs = []
    for pair in li:
        if pair not in forbiddenPairs:
            allowedPairs.append(pair)
    return allowedPairs  
        
def getNeighbours(state):
    neighbours = []
    li_one = []  # one person in boat
    bin = stateToString(state)
    if state < 64:  # boat at left
        for i in range(6):
            if bin[6 - i] == "0":
                li_one.append(i)
        li_two = list(itertools.combinations(li_one, 2)) #two persons in boat
        li_two = removeForbiddenTransfers(li_two)
    else: # boat at right
        for i in range(6):
            if bin[6 - i] == "1":
                li_one.append(i)
        li_two = list(itertools.combinations(li_one, 2))
        li_two = removeForbiddenTransfers(li_two)

    li_values = []
    if state < 64:  # boat at left, restrict to two persons transfer
        for li in li_two:
            li_values.append(2**li[0] + 2**li[1] + 64) 
    else:  # boat at right, one or two persons transfer
        for i in li_one:
            li_values.append(2**i + 64)
        for li in li_two:
            li_values.append(2**li[0] + 2**li[1] + 64) 
   
    for value in li_values:
        v = state ^ value
        if isStateAllowed(v):  # restrict to allowed states
            neighbours.append(v)
    return neighbours

def search(state):
    visited.append(state)  # state marked as visited

    # Check for solution
    if state == targetState:
        solutions.append(visited[:])
        
    for neighbour in getNeighbours(state):
        if neighbour not in visited: # Check if already visited
            search(neighbour) # recursive call
    visited.pop() 

nbSolution = 0             
makeGameGrid(7, 3, 50, None, False, mousePressed = pressEvent)
addStatusBar(30)
setBgColor(Color.white)
setTitle("Searching...")
show()
visited = []
actors = [Actor("sprites/boat.png"), 
   Actor("sprites/man_0.png"), Actor("sprites/woman_0.png"),
   Actor("sprites/man_1.png"), Actor("sprites/woman_1.png"),
   Actor("sprites/man_2.png"), Actor("sprites/woman_2.png")]

left_locations =  [Location(2, 0), 
                   Location(2, 1), Location(2, 2), 
                   Location(1, 1), Location(1, 2), 
                   Location(0, 1), Location(0, 2)] 
right_locations = [Location(4, 0), 
                   Location(4, 1), Location(4, 2), 
                   Location(5, 1), Location(5, 2), 
                   Location(6, 1), Location(6, 2)] 

for i in range(7):
    addActorNoRefresh(actors[i], left_locations[i])
for i in range(3):    
   getBg().fillCell(Location(3, i), Color.blue)   
refresh()

startState = 0
targetState = 127 
solutions = []
search(startState)

maxLength = 0
maxSolution = None
minLength = 100
minSolution = None
for solution in solutions:
    if len(solution) > maxLength:
        maxLength = len(solution)
        maxSolution = solution
    if len(solution) < minLength:
        minLength = len(solution)
        minSolution = solution
setStatusText("#Solutions: " + str(len(solutions)) + ", Min Length: " 
             + str(minLength) + ", Max Length: " + str(maxLength))

setTitle("Press key to cycle")
oldState = startState
for state in minSolution[1:]:
    getKeyCodeWait(True)
    showState(state)
    info = getTransferInfo(oldState, state)
    setTitle("#Transferred: " + str(info))
    oldState = state
setTitle("Done. #Boat Transfers: " + str((len(minSolution) - 1)))

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

MEMENTO

Avec de tels casse-têtes, on ne sait jamais à l’avance s’ils possèdent une ou plusieurs solutions. Il se trouve qu’il est bien plus facile, pour nous humains, de trouver une solution en tâtonnant que de prouver qu’il n’existe pas de solution. Par contre, pour un ordinateur qui effectue une recherche exhaustive de manière systématique, l’énumération de toutes les configurations possibles et de ce fait la recherche de l’ensemble des solutions possibles n’est pas un problème, même si celle-ci peut nécessiter un temps énorme. Cette situation peut malheureusement déjà survenir avec des casse-têtes relativement simples en raison de l’explosion combinatoire, de sorte que l’on touche à nouveau aux limites de la calculabilité et de l’utilisation de l’ordinateur.

Il est intéressant de noter que Bachet avait déjà pu trouver la solution optimale impliquant 11 traversées, ce qui correspond à ce que trouve notre programme. Il développe une argumentation tellement géniale traversée après traversée que la stratégie de résolution du casse-tête en devient évidente. On ne sait par contre pas s’il a d’abord utilisé une approche par tâtonnement et établi seulement par la suite son argumentation ou s’il a pu directement élaborer la solution optimale.

EXERCICES

Résoudre le X-Sudoku suivant. Le X-Sudoku implique comme règle supplémentaire que les nombres 1 à 9 ne doivent apparaître qu’une seule fois dans chacune des grandes diagonales de la grille.

Montrer qu’il n’est pas possible de résoudre le problème des « vilains maris jaloux » si uniquement une personne à la fois peut effectuer la traversée.