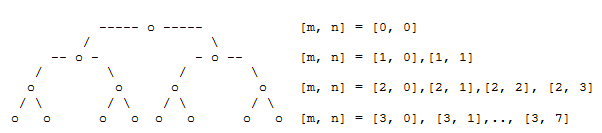INTRODUCTION

Dans le domaine du développement de jeu vidéo, les choses commencent à devenir intéressantes lorsque l’ordinateur devient lui-même un joueur présentant une certaine intelligence. Un tel programme doit non seulement se conformer aux règles du jeu mais également poursuivre une stratégie de victoire. Afin d’implémenter une stratégie de jeu, il faut voir le jeu comme une séquence de situations pouvant être clairement identifiés à l’aide d’une variable appropriée s. Ces situations sont appelées états du jeu, raison pour laquelle la variable s est appelée variable d’état. La stratégie gagnante consiste à passer de l’état initial à un état gagnant dans lequel le jeu est terminé.

Dans cette section, nous allons aborder des techniques importantes qui sont valables de manière générale et qui vous aideront à développer des jeux vidéo capables de gagner même contre des joueurs humains très intelligents. Il vous restera cependant encore beaucoup de liberté et d’occasions pour développer vos propres idées ainsi que des stratégies de jeu plus efficaces, plus simples et mieux adaptées qui permettront d’améliorer le jeu encore davantage ou de consommer moins de puissance de calcul.

De plus, il est un fait que de nombreux systèmes politiques, économiques ou sociaux peuvent être compris et modélisés comme des jeux, ce qui vous permettra d’appliquer les notions abordées ci-après dans un panel très large de domaines particulièrement pertinents.

RECHERCHE D’UNE SOLUTION POUR UN JEU EN SOLITAIRE

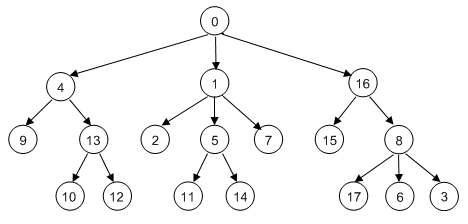
Comme nous l’avons vu précédemment, on peut représenter les états de jeu comme des nœuds dans un graphe qui est parcouru pas à pas. Il faut commencer par déterminer de manière unique les états du jeu selon certains critères tels que l’arrangement des pièces sur le plateau de jeu. Les règles du jeu spécifient quels sont les successeurs (ou voisins) possibles d’un état du jeu particulier. Ces nœuds sont alors reliés dans le graphe par une arête. Puisqu’il s’agit d’états successeurs, les arêtes sont orientées en partant du nœud représentant l’état actuel vers ses successeurs. Un nœud est parfois appelé « père » et ses voisins des « fils » et il est possible qu’il y ait une arête orientée partant de fils pour remonter au père.

Il faut pouvoir stocker l’arbre en entier dans une structure de données appropriée. Une bonne idée est d’utiliser une liste dont chaque élément d’indice i est une sous-liste comprenant les nœuds fils du nœud i. Ainsi, les fils du nœud 0 se trouveront dans la sous-liste placée à la position 0, les fils du nœud 1 figureront dans la sous-liste placée à la position 1, etc … Si un nœud ne possède pas de fils, la liste des nœuds fils correspondante sera vide [plus... Un tel nœud est appelé feuille de l’arbre].

L’arbre illustré ci-dessus peut donc être représenté par la liste suivante:

neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13],[11, 14], [], [], [17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []]

Le fait d’identifier un nœud par un nombre est une astuce qui permet de déterminer facilement ses nœuds fils au sein de la liste grâce à l’indice. L’algorithme permettant de trouver le chemin pour passer d’un nœud à un autre nœud placé plus en profondeur dans l’arbre est défini récursivement dans la fonction search(node). Voici sa formulation en pseudo code :

  search(node):
     if node == targetnode:
          print "Target achieved"
          return
     Déterminer la liste neighbors des voisins de node
     parcourir cette liste et faire pour chacune:
          search(neighbors)

De plus, les nœuds visités sont ajoutés à la fin de la liste visited. Si l’état visé n’est pas atteint avant, le dernier nœud ajouté à la liste visited en est supprimé après que tous ses fils ont été visités. Cela permet de restaurer l’état en vigueur avant la visite infructueuse de ce nœud [plus... La liste visited présente donc une structure de pile (Stack en anglais), à savoir une structure LIFO = Last In First Out) ]. Le nœud de départ et d’arrivée peuvent être saisis au début de l’exécution du programme.

neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13], [11, 14], [], [], 
             [17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []] 

def search(node):
    visited.append(node) # put (push) to stack

    # Check for solution
    if node == targetNode:
        print "Target ", targetNode, "achieved. Path:", visited
        targetFound = True
        return
        
    for neighbour in neighbours[node]:
        search(neighbour) # recursive call
    visited.pop() # redraw (pop) from stack

startNode = -1
while startNode < 0 or startNode > 17:
   startNode = inputInt("Start node (0..17):")
targetNode = -1
while targetNode < 0 or targetNode > 17:
   targetNode = inputInt("Target node (0..17):")
visited = []
search(startNode)

MEMENTO

LA TRAVERSÉE D’UN ALIEN

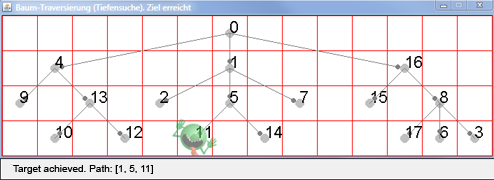
Il serait agréable de pouvoir visualiser l’exécution de l’algorithme en représentant graphiquement l’arbre de décision du jeu et en le traversant progressivement au fur et à mesure du déroulement en pressant sur une touche. Pour ce faire, utilisons une fenêtre GameGrid dans laquelle les nœuds de l’arbre sont représentés par un cercle placé au milieu d’une cellule de la grille (coordonnées grille / grid location).

Un alien semi-transparent met en évidence l’état courant du jeu.

On dessine l’arbre en utilisant les méthodes graphiques de la classe GGBackground. Pour montrer la direction des arêtes, il est possible d’ajouter un petit cercle aux arêtes en lieu et place d’une pointe de flèche en utilisant la méthode getMarkerPoint(). Il faut alors s’assurer de rafraîchir l’écran avec refresh(). La barre d’état montre des informations importantes.

from gamegrid import *

neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13], [11, 14], [], [], 
             [17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []] 

locations = [Location(6, 0), Location(6, 1), Location(4, 2), Location(13, 3),
             Location(1, 1), Location(6, 2), Location(12, 3), Location(8, 2),
             Location(12, 2), Location(0, 2), Location(1, 3), Location(5, 3),
             Location(3, 3), Location(2, 2), Location(7, 3), Location(10, 2), 
             Location(11, 1), Location(11, 3)]

def drawGraph():
    getBg().clear()
    for i in range(len(locations)):
        getBg().setPaintColor(Color.lightGray)
        getBg().fillCircle(toPoint(locations[i]), 6) 
        getBg().setPaintColor(Color.black)
        getBg().drawText(str(i), toPoint(locations[i]))
        for k in neighbours[i]:
            drawConnection(i, k)
    refresh()

def drawConnection(i, k):
    getBg().setPaintColor(Color.gray)
    startPoint = toPoint(locations[i])
    endPoint = toPoint(locations[k])
    getBg().drawLine(startPoint, endPoint) 
    getBg().fillCircle(getMarkerPoint(endPoint, startPoint, 10), 3)

def search(node):
    global targetFound
    if targetFound:
        return
    visited.append(node) # put (push) to stack
    alien.setLocation(locations[node])
    refresh()
    if node == targetNode:
        setStatusText("Target " + str(targetNode) + "achieved. Path: " 
                      + str(visited))
        targetFound = True
        return
    else:
        setStatusText("Current node " + str(node) + " .  Visited: " 
        + str(visited))
    getKeyCodeWait(True) # exit if GameGrid is disposed
  
    for neighbour in neighbours[node]:
        search(neighbour)  # Recursive call
    visited.pop()
    
makeGameGrid(14, 4, 50, Color.red, False)
setTitle("Tree-traversal (depth-first search). Press a key...")
addStatusBar(30)
show()
setBgColor(Color.white)
drawGraph()
 
startNode = -1
while startNode < 0 or startNode > 17:
   startNode = inputInt("Start node  (0..17):")  
targetNode = -1
while targetNode < 0 or targetNode > 17:
   targetNode = inputInt("Target node  (0..17):")

visited = []
targetFound = False
alien = Actor("sprites/alieng_trans.png")
addActor(alien, locations[startNode])

search(startNode)
setTitle("Tree-traversal (depth-first search). Target achieved")

MEMENTO

L’ALIEN SUR LE CHEMIN DU RETOUR

Afin de rendre visible le chemin emprunté par l’alien lors de son retour sur trace, il est nécessaire de sauvegarder la séquence des nœuds visités lors du parcours en profondeur. Le passage à chaque niveau de profondeur supplémentaire engendre une nouvelle liste que l’on sauvegarde dans stepsList. Après avoir effectué un retour sur trace, il faut supprimer la dernière entrée de cette liste avec stepsList.pop().

from gamegrid import *

neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13], [11, 14], [], [], 
             [17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []] 

locations = [Location(6, 0), Location(6, 1), Location(4, 2), Location(13, 3),
             Location(1, 1), Location(6, 2), Location(12, 3), Location(8, 2),
             Location(12, 2), Location(0, 2), Location(1, 3), Location(5, 3),
             Location(3, 3), Location(2, 2), Location(7, 3), Location(10, 2), 
             Location(11, 1), Location(11, 3)]

def drawGraph():
    getBg().clear()
    for i in range(len(locations)):
        getBg().setPaintColor(Color.lightGray)
        getBg().fillCircle(toPoint(locations[i]), 6) 
        getBg().setPaintColor(Color.black)
        getBg().drawText(str(i), toPoint(locations[i]))
        for k in neighbours[i]:
            drawConnection(i, k)
    refresh()

def drawConnection(i, k):
    getBg().setPaintColor(Color.gray)
    startPoint = toPoint(locations[i])
    endPoint = toPoint(locations[k])
    getBg().drawLine(startPoint, endPoint) 
    getBg().fillCircle(getMarkerPoint(endPoint, startPoint, 10), 3)

   

def search(node):
    global targetFound
    if targetFound:
        return
    visited.append(node) # put (push) to stack
    alien.setLocation(locations[node])
    refresh()
    if node == targetNode:
        setStatusText("Target " + str(targetNode) + "achieved. Path: " 
                      + str(visited))
        targetFound = True
        return
    else:
        setStatusText("Current nodes " + str(node) + " .  Visited: " 
                      + str(visited))
    getKeyCodeWait(True) # exit if GameGrid is disposed
  
    for neighbour in neighbours[node]:
        steps = [node]
        stepsList.append(steps)
        steps.append(neighbour)
        search(neighbour)  # Recursive call
        steps.reverse()
        if not targetFound:
            for loc in steps[1:]:
                setStatusText("Go back")
                alien.setLocation(locations[loc])
                refresh()
                getKeyCodeWait()
        stepsList.pop()
    visited.pop()
    
makeGameGrid(14, 4, 50, Color.red, False)
setTitle("Tree-traversal (depth-first search). Press a key...")
addStatusBar(30)
show()
setBgColor(Color.white)
drawGraph()
 
startNode = -1
while startNode < 0 or startNode > 17:
   startNode = inputInt("Start node  (0..17):")  
targetNode = -1
while targetNode < 0 or targetNode > 17:
   targetNode = inputInt("Target node (0..17):")

visited = []
stepsList = []
targetFound = False
alien = Actor("sprites/alieng_trans.png")
addActor(alien, locations[startNode])

search(startNode)
setTitle("Tree-traversal (depth-first search). Target  achieved")

MEMENTO

STATÉGIE DANS UN LABYRINTHE

Il est parfois très difficile, voire même angoissant, de parvenir à trouver le chemin menant à la sortie d’un labyrinthe. Heureusement, grâce à vos connaissances sur le retour sur trace, vous êtes maintenant en mesure d’écrire un programme capable de trouver la sortie à tous les coups pour autant que celle-ci existe. Il est relativement évident qu’il est possible de modéliser un labyrinthe ne possédant pas de cycle par un arbre. Il apparaît donc que de trouver la sortie d’un tel labyrinthe correspond en fait à traverser un arbre.

Dans le cas présent, nous allons nous contenter d’un petit labyrinthe aléatoire de 11x11 cellules. L’alien se déplace d’une seule étape à chaque pression d’une touche du clavier mais recherche directement la sortie de manière autonome lors d’une pression sur la touche Enter.

Le labyrinthe est généré à l’aide de la classe Maze dont le constructeur prend en argument des entiers impairs représentant le nombre de lignes et de colonnes désirées. À chaque fois, la classe génère un labyrinthe aléatoire différent dont l’entrée se trouve en haut à gauche et la sortie en bas à droite. La méthode isWall(loc) permet de tester si la position loc correspond à un mur.

Il n’est souvent pas souhaitable de déterminer le graphe de jeu complet avant le début du jeu. Très souvent, cela est même impossible puisqu’il y aurait tant de situations à prévoir qu’il faudrait un temps CPU et un stockage dans la RAM complètement démesuré. De ce fait, il est souvent préférable de ne déterminer les nœuds fils du nœud courant que lors du parcours de l’arbre. En l’occurrence, on détermine les nœuds voisins du nœud actuel en sélectionnant les cellules adjacentes (au maximum 4) qui ne sont pas des murs et qui ne se situent pas en dehors de la grille.

from gamegrid import *

def createMaze():
    global maze
    maze = GGMaze(11, 11)
    for x in range(11):
        for y in range(11):
            loc = Location(x, y)
            if maze.isWall(loc):
                getBg().fillCell(loc, Color(0, 50, 0))
            else:    
                getBg().fillCell(loc, Color(255, 228, 196))
    refresh()

def getNeighbours(node):
    neighbours = []
    for loc in node.getNeighbourLocations(0.5):
        if isInGrid(loc) and not maze.isWall(loc):
           neighbours.append(loc)
    return neighbours
    
def search(node):
    global targetFound, manual
    if targetFound:
        return
    visited.append(node)  # push
    alien.setLocation(node)
    refresh()
    delay(500)
    if manual:
        if getKeyCodeWait(True) == 10:  #Enter
            setTitle("Finding target...")
            manual = False

    # Check for termination
    if node == exitLocation:
        targetFound = True
        
    for neighbour in getNeighbours(node):
        if neighbour not in visited:
            backSteps = [node]
            backStepsList.append(backSteps)
            backSteps.append(neighbour)

            search(neighbour) # recursive call

            backSteps.reverse()
            if not targetFound:
                for loc in backSteps[1:]:
                    setTitle("Must go back...")
                    alien.setLocation(loc)
                    refresh()
                    delay(500)
                if manual:    
                    setTitle("Went back. Press key...")
                else:
                    setTitle("Went back. Find target...")
            backStepsList.pop()
    visited.pop() # pop

manual = True
targetFound = False
visited = []
backStepsList = []
makeGameGrid(11, 11, 40, False)
setTitle("Press a key. (<Enter> for automatic")
show()
createMaze()
startLocation = maze.getStartLocation()
exitLocation = maze.getExitLocation()
alien = Actor("sprites/alieng.png")
addActor(alien, startLocation)
search(startLocation)
setTitle("Target found")

MEMENTO

EXERCISES

MATÉRIAL SUPPLÉMENTAIRE

LE PROBLÈME DES N DAMES

Le problème des N dames est un problème d’échecs qui a déjà été discuté depuis le milieu du 19e siècle. Il s’agit de placer N dames sur un échiquier de taille N fois N de telle sorte qu’elles ne se menacent pas mutuellement selon les règles habituelles des échecs qui stipulent que la dame se peut se déplacer horizontalement, verticalement et en diagonale. Ce problème appelle deux types de solutions dont les niveaux de difficulté sont radicalement différents. La solution la plus facile à obtenir consiste à trouver un placement particulier des dames qui satisfait les contraintes du problème. L’autre type de solution, beaucoup plus difficile à atteindre, consiste à déterminer le nombre de placements possibles. Le mathématicien Glaisher a prouvé en 1874 déjà que le problème des N dames comportait 92 solutions pour un échiquier habituel, à savoir pour N=8.

Le problème des N dames est considéré comme un candidat classique pour la résolution par retour sur trace. Il s’agit de placer les dames une à une sur l’échiquier de telle sorte que chaque nouvelle dame placée ne menace aucune dame placée précédemment. Si l’on procède de manière naïve, il y a tôt ou tard un moment où l’on ne peut plus placer de dame. La stratégie du retour sur trace consiste alors à supprimer la dernière dame placée pour tenter une alternative. Si cette nouvelle tentative ne mène toujours pas à une solution, il faut encore retirer une dame de plus et ainsi de suite, jusqu’à ce qu’une solution soit trouvée. Un humain s’emmêlerait vite les pinceaux en perdant le contrôle des solutions déjà testées mais l’ordinateur ne souffre pas de ce problème car il procède de manière purement mécanique et méthodique.

De même que pour toute situation à traiter par retour sur trace, on peut considérer les états de jeu comme des nœuds dans le graphe de jeu. Il est à cet effet crucial de choisir une structure de données appropriée. Procéder par la force brute en testant toutes les façons possibles de placer les N dames sur l’échiquier et en rejetant celles où les dames s’attaquent mutuellement est totalement impensable. En effet, lorsque N vaut seulement 8, il y a déjà environ 422 millions placements possibles à tester.

Il serait bien plus malin de ne considérer dès le début que des positions dans lesquelles chaque dame se trouve seule sur sa colonne et sa rangée. À ce dessein, pour N=8, on peut représenter l’état du jeu en se contentant d’une liste de 8 nombres dont l’élément i représente la position de la dame i dans la rangée i. Les lignes dépourvues de dame sont représentées par le nombre -1. En utilisant des indices de ligne et de colonne compris entre 0 et n-1, le placement représenté ci-contre serait représenté par la liste node = [1, 4, -1, 3, 0, 6, -1, 7].

On peut déterminer les noeuds voisins du nœud actuel (node) au sein de l’algorithme de retour sur trace à l’aide de la fonction getNeighbours(node). On passe de ce fait d’une structure de données unidimensionnelle à la liste Locations qui utilise les coordonnées x et y des cases de l’échiquier. Les cases déjà occupées sont référencées dans la liste squares et celles qui ne peuvent pas être utilisées en vertu des règles des échecs dans la liste forbidden. Il est à cet effet utile de recourir à la méthode getDiagonalLocations(). Finalement, on crée la liste allowed pour stocker les cases qui peuvent encore recevoir une dame. Il faut à ce stade remplacer le -1 dans la liste des nœuds voisins par l’indice de la colonne sur laquelle la nouvelle dame a été placée.

L’algorithme de retour sur trace maintenant bien connu est implémenté dans la fonction search(). Dès qu’une solution a été trouvée, la recherche par retour sur trace est arrêtée (condition d’arrêt de la récursion).

from gamegrid import *

n = 8 # number of queens

def getNeighbours(node):
    squares = [] # list of occupied squares
    for i in range(n):
        if node[i] != -1:
           squares.append(Location(node[i], i))

    forbidden = [] # list of forbidden squares
    for location in squares:
        a = location.x 
        b = location.y
        for x in range(n):
            forbidden.append(Location(x, b))  # same row
        for y in range(n):
            forbidden.append(Location(a, y))  # same column
        for loc in getDiagonalLocations(location, True):   #diagonal up
            forbidden.append(loc)
        for loc in getDiagonalLocations(location, False):  #diagonal down
            forbidden.append(loc)

    allowed = [] # list of all allowed squares = all - forbidden
    for i in range(n):
        for k in range(n):
            loc = Location(i, k)
            if not loc in forbidden:
                allowed.append(loc)

    neighbourNodes = [] 
    for loc in allowed:
        neighbourNode = node[:]
        i = loc.y # row
        k = loc.x # col
        neighbourNode[i] = k 
        neighbourNodes.append(neighbourNode)
    return neighbourNodes        

def search(node):
    global found
    if found or isDisposed(): 
        return
    visited.append(node)  # node marked as visited

    # Check for solution
    if not -1 in node: 
        found = True
        drawNode(node)
        
    for s in getNeighbours(node):
        search(s)
    visited.pop()

def drawBoard():
    for i in range(n):
        for k in range(n):
            if (i + k) % 2 == 0:
                getBg().fillCell(Location(i, k), Color.white)

def drawNode(node):
    removeAllActors()
    for i in range(n):
        addActorNoRefresh(Actor("sprites/chesswhite_1.png"),Location(node[i],i))
    refresh()

makeGameGrid(n, n, 600 // n, False)
setBgColor(Color.darkGray)
drawBoard()
show()
setTitle("Searching. Please wait..." )

visited = []
found = False
startNode = [-1] * n  # all squares empty
search(startNode)
setTitle("Search complete. ")

MEMENTO

EXERCICES