INTRODUCTION

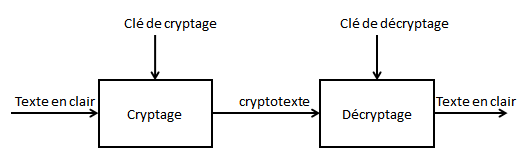
Le principe du secret des données joue un rôle de plus en plus important dans notre société moderne car elle garantit le respect de la vie privée ainsi que la confidentialité des informations gouvernementales, industrielles ou militaires. Pour cela, il est nécessaire de crypter les données de telle sorte que si elles venaient à tomber entre les mains des fausses personnes, il soit impossible ou du moins très difficile de retrouver l’information originale sans que la méthode de cryptage soit compromise au préalable.

Durant l’encodage, les données originales sont transformées en données codées et lors du décodage, les données originales sont restaurées à partir des données cryptées. Si les données originales sont constituées de lettres de l’alphabet, on parle de texte en clair et de cryptotexte.

La description de la méthode utilisée pour effectuer le décryptage est appelée clé qui peut consister simplement en un nombre, une chaine de caractères numériques alphabétiques. Si la même clé est utilisée pour le codage et le décodage, on parle de système à clé symétrique. Si, en revanche, les clés de codage et de décodage sont différentes, on parle de méthode de cryptographie asymétrique (à clé publique).

CHIFFRE DE CÉSAR

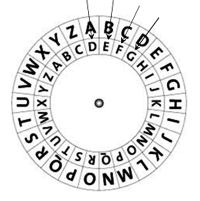
D’après la tradition, Jules César (100 av. J.-C. - 44 av. J.-C.) utilisait déjà la méthode suivante dans ses communications militaires : chaque caractère du texte en clair était décalé dans l’alphabet d’un certain nombre de lettres en reprenant au début de l’alphabet une fois arrivé au bout.

Cette méthode utilisait deux anneaux imbriqués portant les lettres de l’alphabet. L’anneau intérieur était décalé d’un certain nombre de positions, ce qui constitue la clé de cryptage. Par exemple, si la clé vaut 3, le A sera codé par un D, le B par un E, le C par un F, le D par un G etc … Le programme ci-dessous lit le message à crypter depuis un fichier texte pour permettre de le modifier et de le partager facilement. Il faut écrire le texte en clair à l’aide d’un éditeur de code standard dans le fichier original.txt qu’il faut sauvegarder dans le même dossier que le programme Python. Il faut restreindre le message original aux lettres capitales, aux espaces et aux retours à la ligne. On aura par exemple

ON SE RETROUVE AUJOURD HUI A HUIT HEURES
BISOUS
TANIA

La fonction encode(msg) encode la chaine de caractères msg du message issu du fichier texte. Elle procède en remplaçant chaque caractère original par le caractère crypté correspondant, excepté le caractère de retour à la ligne \n.

import string
key = 4
alphabet = string.ascii_uppercase + " "

def encode(text):
    enc = ""
    for ch in text:
        if ch != "\n":
            i = alphabet.index(ch)               
            ch = alphabet[(i + key) % 27]
        enc += ch
    return enc
    
fInp = open("original.txt")
text = fInp.read()
fInp.close() 

print("Original:\n", text)
krypto = encode(text)
print("Krypto:\n", krypto)

fOut = open("secret.txt", "w")    
for ch in krypto:
    fOut.write(ch)
fOut.close()      

Voici le texte crypté:

SRDWIDVIXVSYZIDEYNSYVHDLYMDEDLYMXDLIYVIW
FMWSYW
XERME

Le décodage est implémenté de façon analogue à part le fait que les caractères sont décalés dans l’autre sens

import string
key = 4
alphabet = string.ascii_uppercase + " "

def decode(text):
    dec = ""
    for ch in text:
        if ch != "\n":
            i = alphabet.index(ch)          
            ch = alphabet[(i - key) % 27]
        dec += ch
    return dec

fInp = open("secret.txt")
krypto = fInp.read()
fInp.close() 

print("Krypto:\n", krypto)
msg = decode(krypto)
print("Message:\n", msg)

fOut = open("message.txt", "w")    
for ch in msg:
    fOut.write(ch)
fOut.close()      

MEMENTO

CHIFFRE DE VIGENÈRE

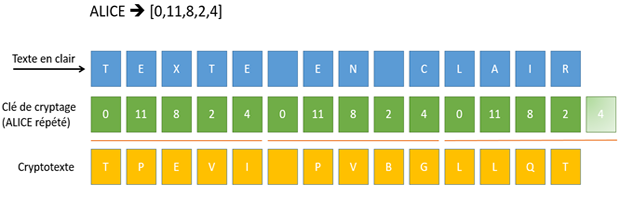
L’illustration suivante permet de mieux comprendre le fonctionnement de la méthode de Vigenère:

import string
key = "ALICE"
alphabet = string.ascii_uppercase + " " 

def encode(text):
    keyList = []
    for ch in key:
        i = alphabet.index(ch)
        keyList.append(i)
    print("keyList:", keyList)
    enc = ""
    for n in range(len(text)):
        ch = text[n]
        if ch != "\n":
            i = alphabet.index(ch)  
            k = n % len(key)                
            ch = alphabet[(i + keyList[k]) % 27]      
        enc += ch
    return enc

fInp = open("original.txt")
text = fInp.read()
fInp.close() 

print("Original:\n", text)
krypto = encode(text)
print("Krypto:\n", krypto)
fOut = open("secret.txt", "w")    
for ch in krypto:
    fOut.write(ch)
fOut.close()     

 Le décodeur est à nouveau pratiquement identique à l’encodeur excepté le sens de décalage.

import string
key = "ALICE"
alphabet = string.ascii_uppercase + " " 

def decode(text):
    keyList = []
    for ch in key:
        i = alphabet.index(ch)
        keyList.append(i)
    print("keyList:", keyList)
    enc = ""
    for n in range(len(text)):
        ch = text[n]
        if ch != "\n":
            i = alphabet.index(ch)  
            k = n % len(key)                
            ch = alphabet[(i - keyList[k]) % 27]      
        enc += ch
    return enc

fInp = open("secret.txt")
krypto = fInp.read()
fInp.close() 

print("Krypto:\n", krypto)
msg = decode(krypto)
print("Message:\n", msg)
fOut = open("message.txt", "w")    
for ch in msg:
    fOut.write(ch)
fOut.close()      

MEMENTO

CRYPTER À L’AIDE DE LA MÉTHODE RSA

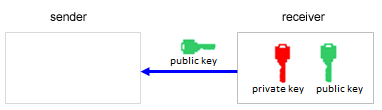
Dans cette méthode dont le nom provient de celui de ses inventeurs, Rivest, Shamir et Adleman, on utilise une paire de clés, à savoir une clé privée et une clé publique. Il s’agit donc d’une méthode de cryptographie asymétrique.

		Étape 1: Le destinataire génère la clé privée ainsi que la clé publique et envoie cette dernière à l’expéditeur.
		Étape 2: L’émetteur encode son message grâce à la clé publique et envoie le texte crypté au destinataire.
		Étape 3: Le destinataire décode le message en utilisant sa clé privée.

Les clés publiques et privées sont générées en utilisant l’algorithme suivant basé sur des résultats de la théorie des nombres [plus...On en trouve une preuve élémentaire dans le livre Barth, Algorithmics for beginners, Springer-Verlag].

On commence par choisir deux nombres premiers p et q qui doivent comporter un très grand nombre de chiffres pour garantir la sécurité du cryptage. On multiplie ensuite ces deux nombres pour obtenir m = p*q. On sait de la théorie des nombres que l’indicatrice d’Euler φ(m) = (p-1)*(q-1) correspond au nombre d’entiers n inférieurs à m qui sont copremiers avec m (a et b sont dits premiers entre eux ou copremiers si et seulement si pgcd(m, n) = 1).

On choisit ensuite un nombre e inférieur à φ(m) tel que e et φ(m) sont premiers entre eux. La paire de nombres (m, e) constitue déjà la clé publique:

Clé publique: [m, e]

Voici un exemple de calcul de la clé publique pour les petits nombres premiers p = 73 et q = 15 :

m = 73 * 151 = 11023,    φ = 72 * 150 = 10800,    e = 11 (choisi copremier avec φ)

Clé publique: [m, e] = [11023, 11]

La clé privée est quant à elle formée de la paire de nombres:

Clé privée: [m, d]

Où d est en entier tel que (d * e) mod φ = 1.

(Puisque e et φ(m)sont premiers entre eux, l’identité de Bézout affirme que cette équation possède nécessairement au moins une solution).

On peut déterminer le nombre d à partir des valeurs de e et φà l’aide d’un simple programme qui va tester 100'000 valeurs pour d au sein d’une boucle:

e = 11
phi = 10800

for d in range(100000):
    if  (d * e) % phi == 1:
        print "d", d

On obtient ainsi plusieurs solutions : (5891, 16691, 27491, 49091, etc.). Comme il suffit d’une seule valeur pour déterminer la clé privée, la première rencontrée fait l’affaire.

Clé privée: [m, d] = [11023, 5891]

Dans le cas présent, il est très facile de déterminer la clé privée uniquement à cause du fait que l’on connaît les nombres premiers p et q et, de ce fait, la valeur de φ. Cependant, sans la connaissance de ces nombres, il faut une puissance de calcul énorme pour calculer la clé privée.

L’algorithme RSA est utilisé pour encoder des nombres. Pour encoder du texte, on utilise donc le code ASCII de chacun des caractères du message en clair qui sera crypté à l’aide de la clé publique [m, s] selon la formule

s = r^e (modulo m).

Le programme suivant écrit chacun des caractères encodés sur une nouvelle ligne dans le fichier secret.txt.

publicKey = [11023, 11]

def encode(text):
    m = publicKey[0]
    e = publicKey[1]
    enc = ""
    for ch in text:
        r = ord(ch)
        s = int(r**e % m)
        enc += str(s) + "\n"
    return enc

fInp = open("original.txt")
text = fInp.read()
fInp.close() 

print("Original:\n", text)
krypto = encode(text)
print("Krypto:\n", krypto)
fOut = open("secret.txt", "w")    
for ch in krypto:
    fOut.write(ch)
fOut.close()      

Le décodeur commence par charger ligne à ligne les nombres présents dans le fichier secret.txt pour les stocker dans une liste. Pour chacun des nombres présents dans cette liste, le nombre original est calculé à l’aide de la clé privée s selon la formule

r = s^d (modulo m).

Ce nombre correspond au code ASCII du caractère original.

privateKey = [11023, 5891]

def decode(li):
    m = privateKey[0]
    d = privateKey[1]
    enc = ""
    for c in li:
        s = int(c)
        r = s**d % m
        enc += chr(r)
    return enc

fInp = open("secret.txt")
krypto = []
while True:
   line = fInp.readline().rstrip("\n")
   if line == "":
       break
   krypto.append(line)
fInp.close() 

print("Krypto:\n", krypto)
msg = decode(krypto)
print("Message:\n", msg)
fOut = open("message.txt", "w")    
for ch in msg:
    fOut.write(ch)
fOut.close()    

MEMENTO

EXERCICES