10.4 PLUS COURT CHEMIN, PROBLÈME DES 3 RÉCIPIENTS
![]()
INTRODUCTION |
De nombreuses solutions algorithmiques ont été développées à partir de l’expérience quotidienne, y compris le retour sur trace. Comme vous l’avez compris, l’ordinateur choisit un coup parmi tous les coups permis et poursuit ainsi de manière parfaitement mécanique et cohérente. Si l’ordinateur se retrouve bloqué dans une impasse, il annule les coups précédents. Cette stratégie s’apparente au tâtonnement dans le contexte de la vie quotidienne et il est bien connu qu’elle n’est souvent pas optimale du tout. Il serait bien préférable de choisir le prochain coup le plus intelligent possible pour se rapprocher du but recherché [plus... En informatique, on appelle cela une recherche heuristique].
|
GRAPHES COMPORTANT DES CYCLES |
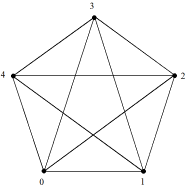
Lors du parcours d’un graphe, il peut arriver que l’on se retrouve en un nœud qui a déjà été visité quelques étapes plus tôt. Prenons l’exemple du réseau de métro souterrain d’une grande métropole dont les gares comportent de nombreuses liaisons différentes. Ce réseau permet d’atteindre une gare A à partir d’une gare B de différentes manières et l’on pourrait rapidement se retrouver à tourner en rond sans jamais atteindre la gare souhaitée. Prenons l’exemple du graphe suivant comportant 5 nœuds tous reliés deux à deux par une arête.
def getNeighbours(node): return range(0, node) + range(node + 1, 5) def search(node): global nbSolution visited.append(node) # node marked as visited # Check for solution if node == targetNode: nbSolution += 1 print nbSolution, ". Route:", visited # don't stop to get all solutions for neighbour in getNeighbours(node): if neighbour not in visited: # Check if already visited search(neighbour) # recursive call visited.pop() startNode = 0 targetNode = 4 nbSolution = 0 visited = [] search(startNode)
|
MEMENTO |
|
En vérifiant au préalable si un nœud a déjà été visité, il est possible d’utiliser le retour sur trace dans un graphe comportant des cycles. Si l’on oublie d’effectuer cette vérification, le programme va se planter et lever une erreur d’exécution due à un débordement de la pile d’appels récursifs (appels récursifs infinis). |
PLUS COURT CHEMIN, SYSTÈME DE NAVIGATION |
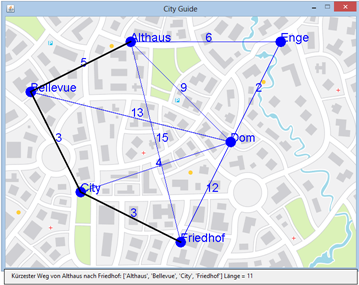
Chercher son chemin pour passer d’un point A à un point de destination B est un problème récurrent dans la vie quotidienne. Comme il y a de nombreux chemins qui mènent de A à B (et non seulement à Rome), il est également important de déterminer un certain critère (longueur du chemin, durée du voyage, qualité de la route, paysages, coûts etc…) dans le but de trouver le chemin optimal [plus... Trouver le plus court chemin d’après un certain critère d’optimalité constitue un algorithme Dans le programme développé ci-après, on se concentre sur les bases. Il traite le cas d’un réseau de métro ne comportant que 6 arrêts dans une ville fictive. Les nœuds du graphe sont identifiés par le nom des stations qui commencent par les lettres A, B, C, D, E et F. On aurait donc également pu identifier les stations par les lettres A, B, C, D, E, F ou par un numéro de station. Pour stocker les relations de voisinage entre stations, on utilise un dictionnaire dont chaque élément est constitué d’une station en guise de clé et de la liste de toutes les stations qui lui sont adjacentes dans le réseau en guise de valeur. Au lieu d’utiliser une fonction getNeighbours(), ont fait directement usage d’un dictionnaire neighbours. De manière similaire, les distances séparant les stations sont stockées dans un autre dictionnaire distances analogue au dictionnaire neighbours. Il faut également recourir à un dictionnaire locations pour stocker les coordonnées x et y des emplacements des stations. L’essentiel du programme est une copie exacte de l’algorithme de retour sur trace utilisé précédemment. De plus, il faut également quelques fonctions auxiliaires pour permettre la représentation graphique.
from gamegrid import * neighbours = { 'Althaus':['Bellevue', 'Dom', 'Enge', 'Friedhof'], 'Bellevue':['Althaus', 'City', 'Dom'], 'City':['Bellevue', 'Dom', 'Friedhof'], 'Dom':['Althaus', 'Bellevue', 'City', 'Enge', 'Friedhof'], 'Enge':['Althaus', 'Dom'], 'Friedhof':['Althaus', 'City', 'Dom']} distances = { ('Althaus', 'Bellevue'):5, ('Althaus', 'Dom'):9, ('Althaus', 'Enge'):6, ('Althaus', 'Friedhof'):15, ('Bellevue', 'City'):3, ('Bellevue', 'Dom'):13, ('City', 'Dom'):4, ('City', 'Friedhof'):3, ('Dom', 'Enge'):2, ('Dom', 'Friedhof'):12} locations = { 'Althaus':Location(2, 0), 'Bellevue':Location(0, 1), 'City':Location(1, 3), 'Dom':Location(4, 2), 'Enge':Location(5, 0), 'Friedhof':Location(3, 4)} def getNeighbourDistance(station1, station2): if station1 < station2: return distances[(station1, station2)] return distances[(station2, station1)] def totalDistance(li): count = 0 for i in range(len(li) - 1): count += getNeighbourDistance(li[i], li[i + 1]) return count def drawGraph(): getBg().clear() getBg().setPaintColor(Color.blue) for station in locations: location = locations[station] getBg().fillCircle(toPoint(location), 10) startPoint = toPoint(location) getBg().drawText(station, startPoint) for s in neighbours[station]: drawConnection(station, s) if s < station: distance = distances[(s, station)] else: distance = distances[(station, s)] endPoint = toPoint(locations[s]) getBg().drawText(str(distance), getDividingPoint(startPoint, endPoint, 0.5)) refresh() def drawConnection(startStation, endStation): startPoint = toPoint(locations[startStation]) endPoint = toPoint(locations[endStation]) getBg().drawLine(startPoint, endPoint) def search(station): global trackToTarget, trackLength visited.append(station) # station marked as visited # Check for solution if station == targetStation: currentDistance = totalDistance(visited) if currentDistance < trackLength: trackLength = currentDistance trackToTarget = visited[:] for s in neighbours[station]: if s not in visited: # if all are visited, recursion returns search(s) # recursive call visited.pop() # station may be visited by another path def init(): global visited, trackToTarget, trackLength visited = [] trackToTarget = [] trackLength = 1000 drawGraph() makeGameGrid(7, 5, 100, None, "sprites/city.png", False) setTitle("City Guide") addStatusBar(30) show() init() startStation = "" while not startStation in locations: startStation = inputString("Start station") targetStation = "" while not targetStation in locations: targetStation = inputString("Target station") search(startStation) setStatusText("Shortest way from " + startStation + " to " + targetStation + ": " + str(trackToTarget) + " Length = " + str(trackLength)) for i in range(len(trackToTarget) - 1): s1 = trackToTarget[i] s2 = trackToTarget[i + 1] getBg().setPaintColor(Color.black) getBg().setLineWidth(3) drawConnection(s1, s2) refresh()
|
MEMENTO |
|
La recherche du plus court chemin au sein d’un graph constitue l’une des tâches élémentaires de la science de l’information. La solution que nous avons étudiée pour déterminer le plus court chemin atteint son but par retour sur trace mais présente le désavantage d’être extrêmement gourmande en ressources CPU. Il existe de bien meilleurs algorithmes pour trouver le plus court chemin qui évitent d’explorer systématiquement tous les chemins possibles. Le plus fameux d’entre eux est appelée "algorithme de Dijkstra". |
LE PROBLÈME DES TROIS JERRICANS |
Les casse-têtes consistant à diviser une quantité donnée en une fraction d’elle-même par mesure (en pesant, versant, etc …) fourmillent depuis des lustres dans les livres pour enfants et dans les magazines. Le célèbre problème des trois récipients est attribué au mathématicien français du 17e siècle Bachet de Méziriac et s’énonce comme suit:
D’après la formulation du problème, il ne s’agit pas seulement de trouver la solution, ce qui est tout à fait faisable en réfléchissant la moindre, mais de déterminer toutes les solutions possibles et de trouver la plus courte. Sans ordinateur, cette tâche serait très fastidieuse. Rechercher toutes les solutions possibles comme dans le cas présent constitue une recherche exhaustive. Pour commencer, on procède par retour sur trace, ce qui nécessite l’élaboration d’une structure de données appropriées pour stocker les états du jeu. Pour ce faire, on utilisera une liste de trois nombres décrivant le niveau de remplissage de chacun des récipients. L’état [1, 4, 3] signifie donc que le récipient de 8 litres contient 1 litre de vin, le récipient de 5 litres en contient 4 et le récipient de 3 litres en contient 3. Une fois n’est pas coutume, on modélise les états du jeu par des nœuds dans un graphe et l’on considère le transfert des récipients vers un autre commune une transition d’un nœud du graphe vers un nœud qui lui est adjacent. Dans cette situation, comme dans tant d’autres, il est insensé de vouloir construire dès le début tout l’arbre de décision. Il est en effet préférable de ne déterminer les nœuds voisins du nœud actuel node par la fonction getNeighbours(node) que lorsque cela est nécessaire. Il faut partir de la considération suivante: Peu importe la quantité de vin présente dans un récipient, il y a essentiellement 6 options différentes de transfert d’un récipient à l’autre. Pour chaque récipient, on peut soit vider totalement son contenu dans un autre récipient ou ne transférer que la quantité de vin correspondant au volume encore disponible dans le récipient de destination. On rassemble donc les nœuds correspondant à ces 6 possibilités de transfert dans la liste neighbours au sein de la fonction getNeighbours(). Pour déterminer les nœuds voisins de l’état courant, la fonction transfer(state, source, target) retourne l’état résultant d’un transfert du récipient source vers target. On considère pour ce faire autant la contenance maximale des récipients que le volume de vin qu’ils contiennent déjà. Encore une fois, la fonction récursive search() utilise l’algorithme de retour sur trace. def transfer(state, source, target): # Assumption: source, target 0..2, source != target s = state[:] # clone if s[source] == 0 or s[target] == capacity[target]: return s # source empty or target full free = capacity[target] - s[target] if s[source] <= free: # source has enough space in target s[target] += s[source] s[source] = 0 else: # target is filled-up s[target] = capacity[target] s[source] -= free return s def getNeighbours(node): # returns list of neighbours neighbours = [] t = transfer(node, 0, 1) # from 0 to 1 if t not in neighbours: neighbours.append(t) t = transfer(node, 0, 2) # from 0 to 2 if t not in neighbours: neighbours.append(t) t = transfer(node, 1, 0) # from 1 to 0 if t not in neighbours: neighbours.append(t) t = transfer(node, 1, 2) # from 1 to 2 if t not in neighbours: neighbours.append(t) t = transfer(node, 2, 0) # from 2 to 0 if t not in neighbours: neighbours.append(t) t = transfer(node, 2, 1) # from 2 to 1 if t not in neighbours: neighbours.append(t) return neighbours def search(node): global nbSolution visited.append(node) # Check for solution if node == targetNode: nbSolution += 1 print nbSolution, ". Route:", visited, ". Length:", len(visited) for s in getNeighbours(node): if s not in visited: search(s) visited.pop() capacity = [8, 5, 3] startNode = [8, 0, 0] targetNode = [4, 4, 0] nbSolution = 0 visited = [] search(startNode) print "Done. Find the best solution!"
|
MEMENTO |
|
Les solutions sont écrites dans la console et ne figurent pas dans ce texte pour vous permettre d’appréhender le problème sans a priori et de tenter de trouver les solutions par vous-mêmes avec un papier et un crayon. Après les avoir découvertes, vous constaterez qu’il y a 16 solutions dont la plus longue nécessite 16 transferts. |
EXERCISES |
|
MATÉRIAL SUPPLÉMENTAIRE |
SYSTÈME DE NAVIGATION URBAIN À L’AIDE DE LA SOURIS |
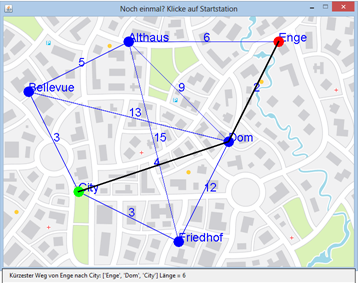
L’expérience utilisateur (UX = User eXperience) joue un rôle primordial dans n’importe quelle application professionnelle. Lors de la phase de conception, le développeur ou le concepteur ne doit pas tant se laisser guider par des considérations d’ordre techniques du domaine de la programmation mais bien plutôt en se mettant dans la peau d’un utilisateur lambda qui veut pouvoir utiliser l’application de la manière la plus intuitive possible et en ne recourant qu’à son bon sens. De nos jours, cela implique des interfaces intégrant une surface contrôlable à l’aide de la souris ou de gestes tactiles. Le développement de l’interface utilisateur nécessite souvent une partie non négligeable de l’effort global investi dans un projet de développement informatique. Les systèmes de navigation adoptent de plus en plus les interfaces tactiles. Celles-ci adoptent cependant une logique relativement similaire au pilotage par la souris. De ce fait, nous allons modifier notre système de navigation urbain pour ajouter le support de la souris, de telle sorte que l’utilisateur puisse sélectionner le point de départ et celui d’arrivée à l’aide d’un clic de souris. Les résultats seront écrits aussi bien dans la barre de titre de la fenêtre que dans sa barre d’état.
L’interface utilisateur devrait être conçue de telle manière qu’il soit possible de sélectionner plusieurs trajets d’affilée sans avoir à redémarrer le programme. De ce fait, il est nécessaire que le programme soit en mesure de retourner à un état initial bien défini. Ce processus qui est mené à bien par la fonction init() est appelé réinitialisation. Du fait que certains éléments sont initialisés automatiquement au démarrage du système, il n’est en aucun cas trivial d’implémenter à l’aide de fonctions définies par le programme lui-même un système de réinitialisation personnalisé permettant de retourner de manière répétée à un état initial propre. Les erreurs d’initialisation sont de ce fait très courantes en programmation en plus d’être généralement fâcheuses et difficiles à identifier puisque le programme se comporte souvent correctement durant les phases de test et ne commence à montrer des signes de dysfonctionnement que plus tard, lorsqu’il est mis en production.
from gamegrid import * neighbours = { 'Althaus':['Bellevue', 'Dom', 'Enge', 'Friedhof'], 'Bellevue':['Althaus', 'City', 'Dom'], 'City':['Bellevue', 'Dom', 'Friedhof'], 'Dom':['Althaus', 'Bellevue', 'City', 'Enge', 'Friedhof'], 'Enge':['Althaus', 'Dom'], 'Friedhof':['Althaus', 'City', 'Dom']} distances = { ('Althaus', 'Bellevue'):5, ('Althaus', 'Dom'):9, ('Althaus', 'Enge'):6, ('Althaus', 'Friedhof'):15, ('Bellevue', 'City'):3, ('Bellevue', 'Dom'):13, ('City', 'Dom'):4, ('City', 'Friedhof'):3, ('Dom', 'Enge'):2, ('Dom', 'Friedhof'):12} locations = { 'Althaus':Location(2, 0), 'Bellevue':Location(0, 1), 'City':Location(1, 3), 'Dom':Location(4, 2), 'Enge':Location(5, 0), 'Friedhof':Location(3, 4)} def getNeighbourDistance(station1, station2): if station1 < station2: return distances[(station1, station2)] return distances[(station2, station1)] def totalDistance(li): count = 0 for i in range(len(li) - 1): count += getNeighbourDistance(li[i], li[i + 1]) return count def drawGraph(): getBg().clear() getBg().setPaintColor(Color.blue) for station in locations: location = locations[station] getBg().fillCircle(toPoint(location), 10) startPoint = toPoint(location) getBg().drawText(station, startPoint) for s in neighbours[station]: drawConnection(station, s) if s < station: distance = distances[(s, station)] else: distance = distances[(station, s)] endPoint = toPoint(locations[s]) getBg().drawText(str(distance), getDividingPoint(startPoint, endPoint, 0.5)) refresh() def drawConnection(startStation, endStation): startPoint = toPoint(locations[startStation]) endPoint = toPoint(locations[endStation]) getBg().drawLine(startPoint, endPoint) def search(station): global trackToTarget, trackLength visited.append(station) # station marked as visited # Check for solution if station == targetStation: currentDistance = totalDistance(visited) if currentDistance < trackLength: trackLength = currentDistance trackToTarget = visited[:] for s in neighbours[station]: if s not in visited: # if all are visited, recursion returns search(s) # recursive call visited.pop() # station may be visited by another path def getStation(location): for station in locations: if locations[station] == location: return station return None # station not found def init(): global visited, trackToTarget, trackLength visited = [] trackToTarget = [] trackLength = 1000 drawGraph() def pressEvent(e): global isStart, startStation, targetStation mouseLoc = toLocationInGrid(e.getX(), e.getY()) mouseStation = getStation(mouseLoc) if mouseStation == None: return if isStart: isStart = False init() setTitle("Click on destination station") startStation = mouseStation getBg().setPaintColor(Color.red) getBg().fillCircle(toPoint(mouseLoc), 10) else: isStart = True setTitle("Once again? Click on starting station.") targetStation = mouseStation getBg().setPaintColor(Color.green) getBg().fillCircle(toPoint(mouseLoc), 10) search(startStation) setStatusText("Shortest route from " + startStation + " to " + targetStation + ": " + str(trackToTarget) + " Length = " + str(trackLength)) for i in range(len(trackToTarget) - 1): s1 = trackToTarget[i] s2 = trackToTarget[i + 1] getBg().setPaintColor(Color.black) getBg().setLineWidth(3) drawConnection(s1, s2) getBg().setLineWidth(1) refresh() isStart = True makeGameGrid(7, 5, 100, None, "sprites/city.png", False, mousePressed = pressEvent) setTitle("City Guide. Click on starting station.") addStatusBar(30) show() init()
|
MEMENTO |
|
La partie algorithmique impliquant le retour sur trace demeure pratiquement inchangée. L’interface utilisateur impliquant le contrôle avec la souris est par contre relativement complexe malgré les facilités mises à disposition par les fonctions de rappel. L’usage du mot-clé global peut facilement conduire à des erreurs d’initialisation du fait que les variables globales peuvent être créées depuis certaines fonctions et que l’on pourrait facilement oublier de les réinitialiser. |