Impression

deutsch english français Imprimer

3.12 IMPRESSION D‘IMAGES

INTRODUCTION

Dans le chapitre portant sur les graphiques avec la tortue, vous avez déjà appris à faire en sorte que la tortue dessine sur une imprimante haute résolution au lieu de l’écran. De manière similaire, GPanel peut effectuer le rendu d’une image sur une imprimante papier ou une imprimante virtuelle telle qu’un fichier Tiff ou EPS. Pour effectuer une impression, il faut placer les instructions de dessin à l’intérieur d’une fonction dépourvue de paramètre, nommée par exemple doIt(). Lorsque cette fonction est appelée directement, le graphique résultant des instructions qu’elle exécute sera affiché à l’écran tandis qu’il sera envoyé vers l’imprimante en passant cette fonction doIt en paramètre à la fonction printerPlot(doIt). Il est même possible de spécifier un facteur d’échelle k avec printerPlot(doIt, k) qui va causer un rétrécissement de l’image si k < 1 et un agrandissement si k >1.

CONCEPTS DE PROGRAMMATION: Graphiques haute résolution

ROSACES

Les courbes à l’allure de roses remontent au XVIIIe siècle, plus précisément au mathématicien Guido Grandi [plus... Ces courbes sont également appelées des rhodoneas]
Les fonctions génératrices de ces courbes sont exprimées le plus naturellement en coordonnées polaires (ρ, φ) et sont paramétrées par un paramètre n:

ρ = sin(nφ)

On passe aux coordonnées cartésiennes comme d’habitude avec les substitutions:

x = ρ cos(φ)
y = ρ sin(φ)

On obtient une jolie rosace en prenant n = . Elle sort encore bien mieux sur une imprimante qu’à l’écran.

from gpanel import *
import math
  
def rho(phi):
    return math.sin(n * phi)

def doIt():
    phi = 0
    while phi < nbTurns * math.pi:
        r = rho(phi)
        x = r * math.cos(phi)    
        y = r * math.sin(phi)    
        if phi == 0:
          move(x, y)
        else:
          draw(x, y)
        phi += dphi

n = math.sqrt(2)
dphi = 0.01
nbTurns = 100
makeGPanel(-1.2, 1.2, -1.2, 1.2)
doIt()
printerPlot(doIt)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

MEMENTO

Suivant le choix opéré pour le paramètre n, on peut créer différents types de courbes. N’hésitez pas à tester des valeurs entières, rationnelles et même irrationnelles telles que (π, e).

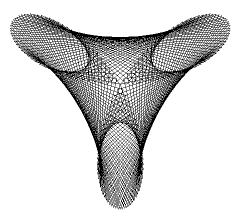
ROSES DE MAURER

Le mathématicien Peter Maurer a introduit ces courbes en 1987 dans son article « A Rose is a Rose... ». Elles se construisent à partir d’une rosace sur laquelle on choisit 360 points connectés entre eux par des segments droits. Les points de la rosace sélectionnés sont tous les points de la forme (sin(nk), k) pour k = 0, d, 2d, 3d, ..., 360d où d correspond à un angle de rotation exprimé en degrés.

Ces points sont ensuite reliés dans l’ordre par des segments droits.

Suivant le choix de n et d, des courbes aux allures totalement différentes vont être engendrées. Il faut les imprimer pour pouvoir les admirer dans toute leur beauté. L’exemple ci-contre peut être généré avec les valeurs n = 3 et d = 47°.

from gpanel import *
import math

def sin(x):
    return math.sin(math.radians(x))

def cos(x):
    return math.cos(math.radians(x))

def cartesian(polar):
    return [polar[0] * cos(polar[1]), polar[0] * sin(polar[1])]         

def rho(phi):
    return sin(n * phi)

def doIt():
    for i in range(361):
        k = i * d
        pt = [rho(k), k]
        corners.append(pt)    
        
    move(cartesian(corners[0]))    
    for pt in corners:
        draw(cartesian(pt))
  
corners = []
n = 3
d = 47
makeGPanel(-1.2, 1.2, -1.2, 1.2)
doIt()
printerPlot(doIt)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller )

MEMENTO

Ce programme utilise des degrés et non des radians. De ce fait, il est pratique de définir ses propres fonctions sinus et cosinus qui prennent des angles en degrés. Cela simplifiera également le code qui ne nécessitera plus de spécifier explicitement le module math dans math.sin ou math.cos pour faire appel aux fonctions trigonométriques.
De manière similaire, il est pratique de définir une conversion des coordonnées polaires aux coordonnées cartésiennes dans la fonction cartesian() où les coordonnées sont passées sous forme de liste à deux éléments.

Le programme stocke les coordonnées polaires des 361 points de la rosace dans la liste corners. À la fin, on les parcourt dans l’ordre en les reliant avec la fonction draw(). D’autres roses de Maurer connues peuvent être obtenues avec les paramètres suivants :

n	d
2	39
2	31
6	71

EXERCICES

Dessiner 50 cercles concentriques de centre center avec la fonction wave(center, wavelength) où wavelength correspond à l’augmentation du rayon entre chaque cercle. On interprétera les cercles dessinés comme les crêtes d’une onde circulaire. Dessiner ensuite les ondes avec un centre légèrement décalé à chaque fois et observer les interférences apparaissant sur une version imprimée de l’image. Quelle courbe connue de la géométrie peut-on alors reconnaître ?