3.8 ART FILAIRE
![]()
INTRODUCTION |
Au lieu de créer ces dessins d’art filaire à la main, on peut aussi confier cette tâche à une machine. Cela impliquerait non seulement que la machine soit capable de comprendre nos instructions, mais encore qu’elle soit capable de les effectuer physiquement, par exemple à l’aide d’un bras robotisé qui puisse tirer des ficelles ou dessiner des traits rectilignes sur un écran. Un tel ensemble d’instructions constitue un algorithme. On pourrait imaginer des instructions de réalisation compréhensibles formulées en langage familier. Mais puisqu’il est souhaitable que la machine effectue exactement les mêmes opérations à chaque fois, l’algorithme doit être formulé de manière très précise, de sorte qu’il n’y ait aucune ambiguïté sur les opérations à effectuer à chaque étape. C’est exactement à cette fin que les langages de programmation ont été inventés et c’est la raison pour laquelle vous devez apprendre un langage de programmation. En effet, les langages naturels ne permettent pas d’écrire une suite précise d’opérations de manière non ambiguë.
|
DES POINTS EN TANT QUE LISTES |
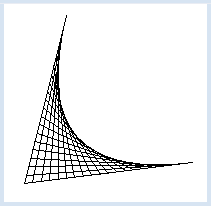
En géométrie, on peut écrire un point par P(x,y) où x et y sont ses coordonnées cartésiennes. Dans le programme, on peut regrouper ces deux nombres x et y dans une structure de données appelée liste. On écrit pour ce faire, p = [x, y]. Le point du plan P(0, 8) est donc modélisé par la liste p = [0, 8] . On peut accéder aux éléments individuels d’une liste par leur indice qui indique leur position dans la liste, en commençant toujours à 0. On écrit l’indice à l’intérieur d’une paire de crochets carrés, à savoir p[0] pour la coordonnée x et p[1] pour la coordonnée y. Ce qui est génial, c’est que l’on peut utiliser cette représentation de points du plan pour toutes les fonctions de GPanel qui nécessitent des coordonnées au lieu de devoir utiliser deux paramètres x et y indépendants. Le programme ci-dessous modélise le fait de tirer des ficelles par des allers-retours depuis le clou en A(0,8) vers le clou en B(0,-8) en passant par 19 clous situés sur l’axe des x. Il introduit un délai avec delay() pour que le traçage des ficelles soit observable par l’oeil humain. from gpanel import * DELAY = 100 def step(x): p1 = [x, 0] draw(p1) delay(DELAY) draw(pB) delay(DELAY) p2 = [x + 1, 0] draw(p2) delay(DELAY) draw(pA) delay(DELAY) makeGPanel(-10, 10, -10, 10) pA = [0, 8] pB = [0, -8] move(pA) for x in range(-9, 9, 2): step(x) |
MEMENTO |
|
Les données doivent également être structurées de manière appropriée dans l’implémentation d’un algorithme. Nos points sont modélisés par des listes de deux éléments représentant les coordonnées cartésiennes. Le choix de la structure de données affecte de manière significative l’ensemble du programme. Un célèbre professeur d’informatique de l’EPFZ a dit de manière très juste : « Programme = algorithme + structure de données » [Ref.] Les listes peuvent stocker de nombreuses valeurs, appelées éléments de la liste, spécifiés dans l’ordre entre crochets carrés. On peut lire les éléments individuels d’une liste grâce à leur indice et leur assigner de nouvelles valeurs. Toutes les commandes graphiques de GPanel fonctionnent également en modélisant les points comme des listes [x, y] représentant les coordonnées cartésiennes. |
PROGRAMMER EST UN ART |
|
MEMENTO |
|
Un algorithme peut être implémenté de différentes manières qui se distinguent de manière significative au niveau de la longueur du code et du temps d’exécution du programme. On peut également parler de programmes plus ou moins élégants. Rappelez-vous seulement pour le moment qu’il n’est pas suffisant pour un programme de produire le résultat correct : l’élégance et le style sont également des critères très importants. Considérez la programmation comme un art ! |
DES ALGORITHMES D’ART FILAIRE ÉLÉGANTS |
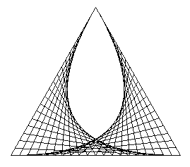
from gpanel import * makeGPanel(0, 100, 0, 100) pA = [10, 10] pB = [90, 20] pC = [30, 90] line(pA, pB) line(pA, pC) r = 0 while r <= 1: pX1 = getDividingPoint(pA, pB, r) pX2 = getDividingPoint(pA, pC, 1 - r) line(pX1, pX2) r += 0.05 delay(300) |
MEMENTO |
|
Les fonctions mises à disposition par des bibliothèques externes, telles que getDividingPoint(), peuvent énormément simplifier un programme. Pour effectuer certaines tâches bien délimitées, vous devriez chercher à recourir à des fonctions de bibliothèques existantes que vous avez déjà rencontrées dans votre expérience de programmation, dénichées dans une documentation ou trouvées sur le Web. Mathématiquement, la courbe émergeant du graphique précédent est une courbe de Bézier quadratique. On peut l’obtenir à l’aide de la fonction quadraticBezier(pB, pA, pC), où pB et pC sont les extrémités et pA est le point de contrôle de la courbe. La notion de courbe de Bézier est expliquée en matériel bonus en fin de section. |
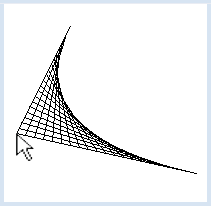
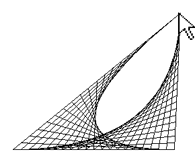
ART FILAIRE PILOTÉ PAR LA SOURIS |
Afin de créer le graphique, on utilise la fonction updateGraphics()qui est appelée par les gestionnaire d'événements de la souris. À chaque fois, on efface toute la fenêtre graphique et on la recrée en tenant compte de la nouvelle position du point A correspondant à la position du curseur de la souris. from gpanel import * def updateGraphics(): clear() line(pA, pB) line(pA, pC) r = 0 while r <= 1: pX1 = getDividingPoint(pA, pB, r) pX2 = getDividingPoint(pA, pC, 1 - r) line(pX1, pX2) r += 0.05 def myCallback(x, y): pA[0] = x pA[1] = y updateGraphics() makeGPanel(0, 100, 0, 100, mousePressed = myCallback, mouseDragged = myCallback) pA = [10, 10] pB = [90, 20] pC = [30, 90] updateGraphics() |
MEMENTO |
|
Il est possible sans problème de gérer deux événements différents, en l’occurrence l’événement de clic et l’événement de glissé (drag), en utilisant une seule fonction de rappel en guise de gestionnaire d’événement. |
EXERCICES |
|
MATÉRIEL EN BONUS |
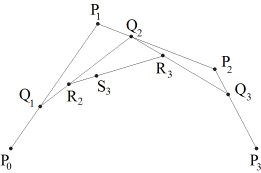
COURBES DE BÉZIER |
On peut facilement implémenter cet algorithme dans un programme Python en représentant les points par des listes et en appelant plusieurs fois la fonction getDividingPoint() au sein de la boucle while qui est contrôlée par le rapport r. from gpanel import * makeGPanel(0, 100, 0, 100) pt1 = [10, 10] pc1 = [20, 90] pc2 = [70, 70] pt2 = [90, 20] setColor("green") line(pt1, pc1) line(pt2, pc2) line(pc1, pc2) r = 0 while r <= 1: q1 = getDividingPoint(pt1, pc1, r) q2 = getDividingPoint(pc1, pc2, r) q3 = getDividingPoint(pc2, pt2, r) line(q1, q2) line(q2, q3) r2 = getDividingPoint(q1, q2, r) r3 = getDividingPoint(q2, q3, r) line(r2, r3) r += 0.05 setColor("black") #cubicBezier(pt1, pc1, pc2, pt2) |
MEMENTO |
|
Une courbe de Bézier cubique est définie par 4 points. Il est possible de dessiner de telles courbes avec la fonction cubicBezier() qui utilisera la couleur et l’épaisseur actuellement définies. |
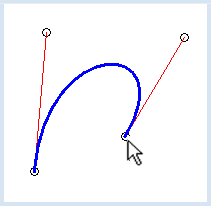
DESSIN INTERACTIF DE COURBES |
Pour déterminer le point que la souris est en train de manipuler, on utilise la variable active: pour stocker la position qu’occupe le point en question au sein de la liste points. Si aucun des points n’est manipulé par la souris, active prend la valeur -1. from gpanel import * def updateGraphics(): # erase all clear() # draw points lineWidth(1) for i in range(4): move(points[i]) if active == i: setColor("green") fillCircle(2) setColor("black") circle(2) # draw tangents setColor("red") line(points[0], points[1]) line(points[3], points[2]) # draw Bezier curve setColor("blue") lineWidth(3) cubicBezier(points[0], points[1], points[2], points[3]) def onMouseDragged(x, y): if active == -1: return points[active][0] = x points[active][1] = y updateGraphics() def onMouseReleased(x, y): active = -1 updateGraphics() def onMouseMoved(x, y): global active active = near(x, y) updateGraphics() def near(x, y): for i in range(4): rsquare = (x - points[i][0]) * (x - points[i][0]) + (y - points[i][1]) * (y - points[i][1]) if rsquare < 4: return i return -1 pt1 = [20, 20] pc1 = [10, 80] pc2 = [90, 80] pt2 = [80, 20] points = [pt1, pc1, pc2, pt2] active = -1 makeGPanel(0, 100, 0, 100, mouseDragged = onMouseDragged, mouseReleased = onMouseReleased, mouseMoved = onMouseMoved) updateGraphics() |
MEMENTO |
|
Il existe des structures de données assez complexes telles que des listes dont les éléments sont eux-mêmes des listes. Dans notre programme, on utilise cela pour stocker une liste de points qui sont eux-mêmes représentés par des listes. On peut alors accéder à la coordonnée x du point P1 en utilisant les doubles crochets points[1][0], thus with double brackets. De nos jours, les courbes de Bézier sont utilisées de manière très abondante dans les programmes de dessin vectoriels et de conception assistée par ordinateur (CAO) [Ref.] |
EXERCICES |
|