Boucles for

deutsch english français Imprimer

3.2 BOUCLES FOR

INTRODUCTION

Souvent, il est nécessaire de maintenir un compteur dans une structure de répétition. Pour ceci, il faut une variable au sein du bloc de répétition qui change d’une certaine quantité à chaque itération de la boucle. Il est plus simple et naturel de réaliser ceci avec une boucle for qu’avec une boucle while. Pour ce faire, il faut tout d’abord apprendre à connaître la fonction range(). Dans le cas le plus simple, range(n) ne prend qu’un seul paramètre également appelé stop value en anglais et retourne une suite de nombres naturels consécutifs débutant à 0 et se terminant à n-1 compris.
Il est utile de tester cette fonction range() dans une session interactive de l’interpréteur. L’appel range(10) va par exemple afficher la liste de nombres

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] dans la fenêtre de sortie. Testez cette fonction avec plusieurs valeurs différentes, parmi lesquelles 0 pour bien comprendre son fonctionnement. Remarquez que la valeur 10 ne figure pas dans la liste de nombres retournés. Ce paramètre 10 indique plutôt le nombre d’éléments présents dans la liste générée.

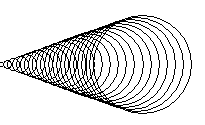
CONCEPTS DE PROGRAMMATION: Itération, structure for, boucles imbriquées.

FAMILLE DE COURBES

On peut dessiner une courbe sympathique à l’aide de 20 segments droits à l’aide d’une boucle for.

from gpanel import *

makeGPanel(0, 20, 0, 20)

for i in range(21):
    line(i, 0, 20, i)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V coller)

MEMENTO

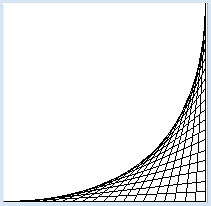
L’instruction for i in range(n) parcourt les nombres de 0 à n-1, à savoir un total de n nombres en tout. Les points de densification des segments droits forment une courbe de Bézier quadratique.

RANGE() AVEC DEUX PARAMÈTRES

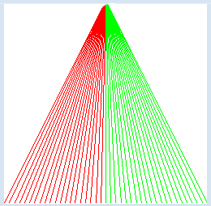
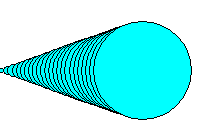
La fonction range peut également prendre deux paramètres. Dans ce cas, le premier indique la valeur de départ de la liste et le second la valeur d’arrêt qui n’est cependant pas incluse dans la liste.

En écrivant par exemple range(2,9), on récupère la liste de nombres [2, 3, 4, 5, 6, 7, 8]. Tester la fonction range sur d’autres couples de paramètres pour bien comprendre son fonctionnement. Tester entre autres les couples suivants : (0,0), (0,1), (1,2), (1,3) et … (5,3) et observer attentivement les listes retournées.

Le programme suivant dessine des segments droits avec deux couleurs différentes contrôlées par le compteur d’itération i. Leur point d’origine se trouve sur l’axe des x (y=0) dont l’abscisse varie entre -20 et 20 par pas de 1. L’extrémité de chaque segment est le point (0, 40).

from gpanel import *

makeGPanel(-20, 20, 0, 40)

for i in range(-20, 21):
    if i < 0:
        setColor("red")
    else:
        setColor("green")    
    line(i, 0, 0, 40)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

MEMENTO

La boucle for i in range(start, stop) avec les entiers start et stop commence à i = start et se termine à i = stop – 1 en augmentant le compteur d’itérations i d’une unité à chaque itération de la boucle. De ce fait, il faut que start soit inférieur à stop pour que le programme puisse entrer dans la boucle puisque range(start, stop) retourne une liste vide si start >= stop.

RANGE() AVEC TROIS PARAMÈTRES

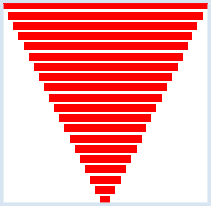
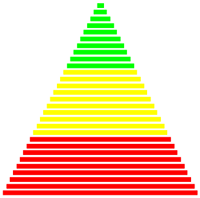
On peut même appeler la fonction range() avec trois paramètres.Dans ce cas, le premier représente la valeur de départ, le deuxième la valeur d’arrêt et le troisième représente l’incrément ajouté à chaque itération au compteur de boucle i. Ce troisième paramètre qui vaut 1 par défaut permet donc de modifier la grandeur du pas de chaque itération.

L’instruction print range(2, 15, 3) va par exemple afficher la liste de nombres [2, 5, 8, 11, 14] dans la fenêtre de sortie du programme.

Dans le graphique ci-contre, on voit une pyramide renversée formée de rectangles pleins. Le plus petit rectangle a une largeur de 2 et le plus grand une largeur de 40. Étudiez attentivement le programme ci-dessous permettant de réaliser cette figure :

from gpanel import *

makeGPanel(0, 40, 0, 40)

setColor("red")
y = 1
for i in range(2, 41, 2):
    move(20, y)
    fillRectangle(i, 1.5)
    y = y + 2

Sélectionner le code source (Ctrl+C pour copier, Ctrl+V pour coller)

MEMENTO

La boucle for i in range(start, stop, step)commence avec i = start et se termine avec une valeur inférieure à stop. Le compteur de boucle i est incrémenté de step à chaque itération de la boucle. Il est également possible de choisir des nombres négatifs pour les paramètres start, stop et step. Si step > 0, il faut que start < stop tandis que si step < 0, il faut que start > stop.

En effet, si step est négatif, i est réduit de step à chaque itération ; la dernière valeur est alors supérieure à stop.

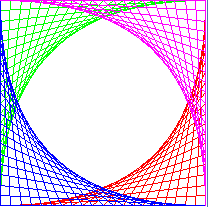
**BOUCLES FOR IMBRIQUÉES (Moiré)**

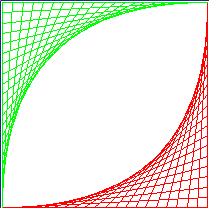
Des lignes serrées disposées les unes au-dessus des autres peuvent faire apparaître des effets optiques appelés Effet de moiré. Dans un carré, on dessine pour chacun des 10 points équidistants situés sur le côté inférieur une ligne issue de ce point et aboutissant sur chacun des 10 points équidistants du côté supérieur. On fait ensuite de même pour les lignes issues des 10 points équidistants du côté gauche vers les points du côté droit.

Étudier attentivement le programme ci-dessous qui utilise à deux reprises le concept de boucles imbriquées.

from gpanel import *

makeGPanel(0, 10, 0, 10)

for i in range(11):
    for k in range(11):
        line(i, 0, k, 10)
        delay(50)
for i in range(11):
    for k in range(11):
        line(0, i, 10, k)
        delay(50)

Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

MEMENTO

Ce programme n’est certainement pas tout simple à comprendre mais il est d’une importance cruciale. Une clé pour le comprendre est de supposer que le compteur i de la boucle extérieure a une valeur constante (initialement 0). La boucle intérieure s’exécute alors avec cette valeur de i en faisant varier k de 0 à 10 non compris, ce qui a pour effet de dessiner les 10 droites issues du point inférieur gauche du carré et aboutissant sur chacun des points équidistants du côté supérieur. Une fois que cette première boucle intérieure est terminée, la boucle extérieure augmente i à 1 pour dessiner les 10 segments issus du point inférieur suivant etc…

La fonction delay(deltaT)met le programme en pause durant deltaT millisecondes, ce qui permet d’observer la manière dont le motif émerge progressivement.

EXERCICES

On obtiendra un graphique encore plus sympathique que celui obtenu dans l’exemple 1 si l’on utilise des couleurs. Dessiner une seconde famille de courbes avec une couleur différente (Figure a).

(a)

(b)

La famille de courbes bleues (Figure b) est dessinée avec line(i, 0, 0, 20 - i). Seriez-vous capables de dessiner également la famille rose ?

Dessiner une famille de cercles vides, puis de disques pleins.

On peut dessiner la famille de cercles coloriés avec la procédure suivante : choisir la couleur cyan, dessiner un disque plein de rayon y, choisir ensuite la couleur noire, dessiner un cercle vide de bord noir de même rayon et continuer ainsi de suite :

   setColor("cyan")
   fillCircle(y)
   setColor("black")
   circle(y)

Dans l’exemple 3, on a dessiné une pyramide renversée. Dessiner une « vraie » pyramide avec trois couleurs. Utiliser pour ce faire une boucle for qui compte les étages pour contrôler le changement de couleur.