deutsch     english    français     Imprimer

 

3.4 FONCTIONS AVEC VALEUR DE RETOUR

 

 

INTRODUCTION

 

Nous avons déjà vu comment définir une fonction avec ou sans paramètre et comment l’appeler. Vous avez sans doute remarqué que le concept de fonction utilisé en programmation diffère sensiblement des fonctions que l’on trouve en mathématiques. En effet, en mathématiques, les fonctions y = f(x) possèdent une variable indépendante et pour chaque valeur de x, la fonction retourne une valeur de la variable dépendante y. Un exemple classique est la fonction quadratique
.  qui, à partir des nombres  x = 0, 1, 2, 3 retourne les carrés 0, 1, 4, 9.

En Python, on peut également définir des fonctions qui calculent des valeurs et les "retournent" sous forme de variables.

CONCEPTS DE PROGRAMMATION: Valeur de retour d’une fonction, discrétisation

 

 

LE MOT-CLÉ RETURN

 

On peut définir une fonction squarenumber(a) qui calcule le carré a * a pour un nombre donné a, exactement comme en mathématiques. La fonction retourne cette valeur avec le mot-clé return. Cela permet d’esquisser le graphe de la fonction dans GPanel. Pour dessiner le graphe, le mieux est d’utiliser draw(x, y) qui dessine des segments droits depuis la dernière position du curseur graphique jusqu’au point (x, y) indiqué en paramètre et qui place ensuite le curseur à la position (x, y). Après l’apparition de la fenêtre GPanel, le curseur graphique se trouve à l’origine (0, 0). Il faut donc ajuster sa position sur le début du graphe avec move() sans quoi le segment de départ sera faux.

   
from gpanel import *
makeGPanel(-25, 25, -25, 25)

def squarenumber(a):
    b = a * a
    return b

for x in range(-5, 6):
    y = squarenumber(x)
    if x == -5:
        move(x, y)
    else:
        draw(x, y)
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

Le mot-clé return, permet à une fonction de retourner une valeur au code appelant et d’interrompre son exécution. Si return est placé avant la fin du bloc, la fonction s’interrompt au et n’exécute pas les instructions qui se trouvent en-dessous du return.

Cependant, comme vous l’avez remarqué, il existe également en informatique des fonctions qui ne retournent pas de valeur et qui produisent tout de même un effet sur l’ensemble du programme. Les fonctions sont même capables de cumuler les deux : retourner une valeur et produire un effet sur l’ensemble du programme, indépendamment de la valeur de retour [plus...Lorsque l’on appelle une telle fonction, on peut très bien ignorer sa valeur de retour et ne l’utiliser que comme une commande].

Cette représentation graphique de la fonction quadratique n’est pas encore satisfaisante. En plus de l’absence de système de coordonnées, le graphe tracé est bien trop anguleux. Cela vient du fait que l’on a évalué la fonction en un nombre trop restreint de points entiers que l’on a ensuite connectés par des segments droits. Cela montre une faiblesse essentielle de l’informatique par rapport aux mathématiques : bien que notre fonction livre pour chaque abscisse x une image y, on ne peut l’évaluer qu’un en nombre fini de points. On dit que l’axe Ox continu est discrétisé ou réparti en points discrets.

 

 

NOMBRES DÉCIMAUX (FLOATS)

 

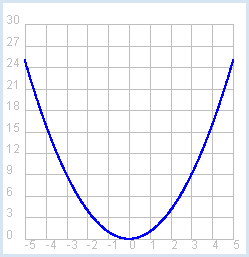
On peut améliorer cette représentation en choisissant de calculer des points plus proches les uns des autres sur l’axe des x. Par exemple, on peut parcourir l’ensemble des abscisses entre -5 et 5 en faisant des centaines de pas. On peut même dessiner un repère cartésien.

Malheureusement, la fonction range utilisée pour contrôler la boucle for n’accepte que des valeurs entières pour la taille des pas. Pour obtenir une meilleure résolution, il faut donc utiliser une boucle while. De cette manière, on peut très bien incrémenter l’abscisse x de 0.01 à chaque pas. Avec ce changement, x n’est plus considéré comme un nombre entier par Python, mais comme un nombre décimal (float).  

   



from gpanel import *
makeGPanel(-6, 6, -3, 33)
setColor("gray")
drawGrid(-5, 5, 0, 30)

def squarenumber(a):
    b = a * a
    return b

setColor("blue")
lineWidth(2)
x  = -5
while x < 5:
    y = squarenumber(x)
    if x == -5:
        move(x, y)
    else:
        draw(x, y)
    x = x + 0.01
Sélectionner le code (Ctrl+C pour copier, Ctrl+V pour coller)

 

 

MEMENTO

 

En Python, les nombres décimaux sont appelées des flottants (float). A contrario des mathématiques, les nombres décimaux ne comptent tous qu’un nombre fini de décimales en informatique. En Python, les flottants sont stockés avec 14 décimales. Dans d’autres langages de programmation, de tels nombres sont appelés double. Un exemple courant est qu’un ordinateur ne pourra jamais vraiment stocker le nombre π dans sa mémoire puisque ce dernier est irrationnel et comporte de ce fait une infinité de décimales sans période. Il faut donc se résoudre à réaliser des calculs avec une précision limitée à 14 décimales au maximum.

Pour dessiner un repère cartésien, procéder de la manière suivante :

  • Étendre le système de coordonnées d’environ 10% horizontalement et verticalement pour permettre l’affichage des étiquettes d’axes. Ainsi, on passera à l’intervalle [-6, 6] pour l’axe x et à [-3, 33] pour l’axe y.
  • Appeler drawGrid() avec les coordonnées que l’on avait l’intention d’utiliser en guise de paramètres. Cela engendre une grille de 10x10 carrés.

 

 

EXERCICES

 
1.

Définir la fonction moyenne(a, b) qui retourne la moyenne arithmétique des deux paramètres. Tester la fonction dans la console.

2.


Examiner le comportement de la fonction y = cos(x). Comment diffère-t-elle de la fonction y = sin(x)?


3.


Afficher le graphe de la fonction y = sin(5x) dans une fenêtre GPanel pour des valeurs de l’axe des x comprises entre 0 et 2π avec une résolution de 0.01. On peut obtenir la valeur de π avec l’identifiant pi disponible dans le module math. Refaire le graphe avec un coefficient de x différent de 5 au sein de la fonction sin. Quelle est l’effet de ce coefficient sur le graphe de la sinusoïde engendrée ?


4.


Définir la fonction f(x) = 1 / sin(x) pour la représenter dans une fenêtre GPanel sur l’intervalle [-5 ;5] (pour les deux axes) avec une résolution de 0.001. Dessiner le système de coordonnées dans une couleur différente. Relever les caractéristiques intéressantes du graphe.