3.10 HASARD ET NOMBRES ALÉATOIRES
![]()
INTRODUCTION |
|
La chance joue un rôle important dans notre vie de tous les jours. On parle de « chance » ou de « hasard » pour désigner les événements qui ne sont pas prédictibles. Si quelqu’un qui ne vous connaît absolument pas vous demande de choisir parmi les couleurs rouge, vert ou bleu, il sera incapable de prévoir à l’avance quelle couleur vous allez choisir, ce qui confère à ce choix un caractère aléatoire. Le hasard joue un rôle très important dans les jeux : lorsque l’on jette un dé, le nombre de points que l’on obtient entre 1 et 6 est complètement aléatoire si le dé n’est pas truqué. L’ordinateur se prête à merveille à la réalisation d’expériences stochastiques car il permet de faire un nombre important d’expériences. Pour cela, l’ordinateur va devoir générer une série de nombres aléatoires qui sont le plus indépendants possible les uns des autres. On utilise le plus souvent des nombres aléatoires entiers pris dans un certain intervalle, par exemple entre 1 et 6, ou des nombres réels compris entre 0 et 1. Un algorithme capable de générer une suite de nombres aléatoires est appelé générateur de nombres aléatoires. Il est très important que tous les nombres générés apparaissent avec la même fréquence à la manière d’un dé non truqué. On dit de tels nombres qu’ils forment une distribution uniforme ou qu’ils sont uniformément distribués.
|
DESSINS ALÉATOIRES |
from gpanel import * from random import randint, random def randomColor(): r = randint(0, 255) g = randint(0, 255) b = randint(0, 255) return makeColor(r, g, b) makeGPanel() bgColor(randomColor()) for i in range(20): setColor(randomColor()) move(random(), random()) a = random() / 2 b = random() / 2 fillEllipse(a, b) |
MEMENTO |
|
La fonction random() retourne des nombres flottants uniformément distribués entre 0 (inclus) et 1 (exclus). Il est nécessaire d’importer le module random pour pouvoir y accéder. Comme nous le verrons en détails dans la section « Traitement d’images » de ce chapitre, les couleurs sont définies par les trois composantes fondamentales rouge, vert et bleu (RVB = RGB = Red, Green, Blue) qui sont combinées par synthèse additive. Les valeurs de chaque composante de couleur sont comprises entre 0 et 255. La fonction randint(start, end) renvoie un nombre aléatoire entier compris entre start et end (Les deux bornes sont incluses). La fonction makeColor() retourne un objet-couleur résultant de la composition des composantes rouge, vert et bleu. |
FRÉQUENCE D’APPARITION AU JET D’UN DÉ |
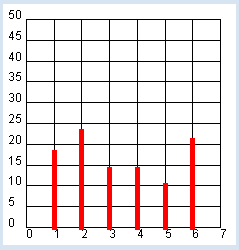
from gpanel import * from random import randint NB_ROLLS = 100 makeGPanel(-1, 8, -0.1 * NB_ROLLS / 2, 1.1 * NB_ROLLS / 2) title("# Rolls: " + str(NB_ROLLS)) drawGrid(0, 7, 0, NB_ROLLS // 2, 7, 10) setColor("red") histo = [0, 0, 0, 0, 0, 0, 0] # hist = [0] * 7 # short form for i in range(NB_ROLLS): pip = randint(1, 6) histo[pip] += 1 lineWidth(5) for n in range(1, 7): line(n, 0, n, histo[n]) |
MEMENTO |
|
On utilise la liste histo pour stocker les fréquences d’apparition des différents événements aléatoires (résultats des dés) en incrémentant l’élément de la liste dont l’indice correspond au résultat obtenu. Pour s’épargner d’inutiles calculs sur les indices, on utilisera une liste de 7 éléments dont le premier, d’indice 0, ne sera jamais utilisé. Quelques expériences de ce type révèlent rapidement que les fréquences d’apparition deviennent de plus en plus uniformes à mesure que le nombre de jets NB_ROLLS. Saugmente, de sorte qu’elles tendent toutes de plus en plus vers 1/6. Mathématiquement, on exprime ce fait de la manière suivante : les issues 1, 2, 3, 4, 5, 6 de l’expérience aléatoire sont équiprobables et leur probabilité d’apparition vaut 1/6. Pour dessiner la grille du repère, il faut faire appel à la fonction drawGrid(xmin, xmax, ymin, ymax, xticks, yticks) comprenant 6 paramètres dont les deux derniers définissent le nombre de subdivisions. Si xmax ou ymax est un nombre flottant, les axes seront libellés avec des nombres flottants. Dans le cas contraire, les axes seront libellés avec des nombres entiers. |
SIMULATIONS MONTE CARLO |
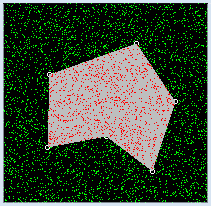
La principauté de Monaco est très célèbre pour ses casinos. Ceux-ci n’ont pas seulement été une attraction pour les célébrités durant les 150 dernières années mais aussi pour les mathématiciens qui tentent d’analyser les jeux de hasard pour échafauder des stratégies de jeu gagnantes. L’ordinateur est bien plus adapté pour tester ces stratégies et plus conciliant que le véritable jeu puisque l’on peut réaliser l’expérience aléatoire sans y laisser des fortunes. Dans le « jeu » suivant, on place des points sur une surface carrée contenant un polygone. On pourrait comparer chaque point à l’impact d’une goutte de pluie. Lorsqu’il pleut, les gouttes sont en principe distribuées de manière uniforme : chaque unité de surface comptera environ le même nombre de gouttes. Pour revenir à notre polygone, on laisse tomber un certain nombre de gouttes sur notre carré et on compte le nombre de gouttes tombées à l’intérieur du polygone. Il est évident que ce nombre sera d’autant plus grand que la surface du polygone sera importante et qu’en moyenne (pour autant qu’il y ait un nombre très élevé de gouttes), ce nombre sera même proportionnel à la surface. Ainsi, si l’aire du polygone vaut ¼ de celle du carré qui l’entoure, ¼ des gouttes tombées dans le carré auront atteint le polygone. Une fois ceci établi, on peut renverser la vapeur pour déterminer le rapport entre la surface du polygone et celle du carré, facilement calculable, en calculant simplement le rapport entre le nombre de gouttes tombées dans le polygone et celles tombées sur l’ensemble du carré.
from gpanel import * from random import random NB_DROPS = 10000 def onMousePressed(x, y): if isLeftMouseButton(): pt = [x, y] move(pt) circle(0.5) corners.append(pt) if isRightMouseButton(): wakeUp() def go(): global nbHit setColor("gray") fillPolygon(corners) setStatusText("Working. Please wait...") for i in range(NB_DROPS): pt = [100 * random(), 100 * random()] color = getPixelColorStr(pt) if color == "black": setColor("green") point(pt) if color == "gray" or color == "red": nbHit += 1 setColor("red") point(pt) setStatusText("All done. #hits: " + str(nbHit) + " of " + str(NB_DROPS)) makeGPanel(0, 100, 0, 100, mousePressed = onMousePressed) addStatusBar(30) setStatusText("Select corners with left button. Start dropping with right button") bgColor("black") setColor("white") corners = [] nbHit = 0 putSleep() go() |
MEMENTO |
Lors du clic gauche de la souris, le programme sauve le sommet ainsi créé dans la liste corners et l’entoure d’un petit cercle servant de marqueur. La simulation de la pluie est effectuée dans la fonction go(). Elle débute lors d’un clic droit et dure un certain laps de temps. Les impacts des gouttes de pluie sont marqués par des points colorés de couleurs différentes suivant qu’ils tombent à l’intérieur ou à l’extérieur du polygone. Si l’on appelait directement la fonction go() depuis la fonction pressCallback(), comme il peut paraître évident de le faire, on ne pourrait voir aucun point avant que la simulation ne se termine. Cela vient du fait que le système empêche le rafraîchissement du graphique depuis un gestionnaire d’événement de la souris pour des raisons qui lui sont propres. Pour visualiser une action de longue durée, il faut donc placer le code ailleurs que dans la fonction de rappel, en général dans le programme principal. L’exécution du programme principal est mise en pause avec putSleep(). Le clic droit réveille le programme principal avec wakeUp(), ce qui va lancer la simulation avec l’appel à go(). De manière générale, pour éviter des surprises désagréables, il faut toujours respecter la règle suivante: Les fonctions de rappel (gestionnaires d’événements) doivent impérativement retourner rapidement à l’appelant. De ce fait, aucune action de longue durée ne devrait prendre place à l’intérieur d’une fonction de rappel, sans quoi l’exécution du programme s’en trouverait bloquée. Pour déterminer si une goutte est tombée à l’intérieur du polygone ou non, il suffit de consulter la couleur du pixel correspondant avec getPixelColorStr() puisque les pixels du polygone sont gris et les autres noirs. Il faut tenir compte également du fait qu’une goutte peut tomber sur un pixel rouge si celui-ci a déjà été précédemment atteint par une goutte. De ce fait, si le pixel atteint est gris ou rouge, on incrémente nbHit by 1 et on colorie le pixel en rouge. Vous pouvez tester cette procédure en générant quelques polygones simples (par exemple des triangles ou des rectangles) et en les mesurant à l’écran avec une règle. Vous constaterez qu’il faut un nombre important de point pour que l’aire estimée avec Monte Carlo corresponde bien à l’aire réelle [plus...Pour gagner une décimal de précision (facteur 10), il faut multiplier par 100 le nombre de points aléatoires]. |
JEU DU CHAOS |
Il peut paraître surprenant de pouvoir créer des motifs réguliers par des expériences aléatoires. Cela vient de la compensation des fluctuations statistiques par un grand nombre d’expériences. Michael Barnsley inventa en 1988 l’algorithme suivant, basé sur la théorie du chaos, qui s’appuie sur une sélection aléatoire des sommets d’un triangle :
from gpanel import * from random import randint MAXITERATIONS = 100000 makeGPanel(0, 10, 0, 10) pA = [1, 1] pB = [9, 1] pC = [5, 8] triangle(pA, pB, pC) corners = [pA, pB, pC] pt = [2, 2] title("Working...") for iter in range(MAXITERATIONS): i = randint(0, 2) pRand = corners[i] pt = getDividingPoint(pRand, pt, 0.5) point(pt) title("Working...Done") |
MEMENTO |
Si l’on a besoin de choisir aléatoirement un objet parmi plusieurs, on les place tous dans une list and pick an object out of it at a random index. Il est assez étonnant que l’on puisse engendrer une figure (appelée triangle de Sierpinski) présentant une grande régularité en choisissant des points aléatoires. |
EXERCICES |
|