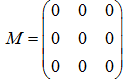8.9 DYNAMIQUE DE GROUPE
![]()
INTRODUCTION |
Les systèmes comportant de nombreux partenaires en interaction sont très répandus. Il est souvent possible de simuler sans problème de tels systèmes à l’aide de programmes informatiques puisque l’ordinateur peut sans autre stocker des milliers ou même des millions d’états individuels tout en suivant leur évolution temporelle. Il va sans dire qu’une telle simulation n’est pas possible avec des systèmes à l’échelle atomique comportant un nombre de particules en interaction de l’ordre de 1023. Ceux-ci dépassent en effet de loin les capacités de stockage et de traitement des ordinateurs. Pour simuler de tels systèmes, il faut utiliser des procédures simplifiées consistant par exemple à diviser le système en plusieurs cellules plus larges. Les simulations des phénomènes liés à l’atmosphère terrestre utilisées pour effectuer les prévisions météorologiques ou les prédictions de l’évolution du climat sur le long terme sont de bons exemples de telles simplifications.
|
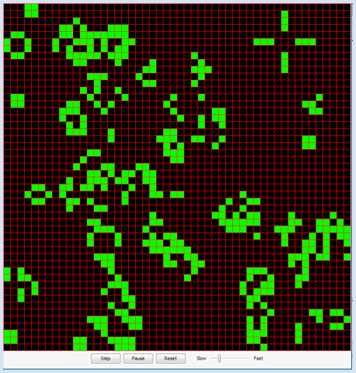
LE JEU DE LA VIE DE CONWAY |
La simulation passe de la génération i à la génération i+1 en considérant, pour chaque cellule, les règles de transitions suivantes basées sur l’état des huit cellules environnantes :
La structure en grille de GameGrid convient à merveille pour implémenter ce jeu. On utilise une liste bidimensionnelle a[x][y] pour encoder l’état de chaque cellule de la population en représentant une cellule morte par un 0 et une cellule vivante par un 1. Le cycle de simulation de GameGrid est considéré comme le temps de vie d’une génération. La population actuelle stockée dans la liste a est copiée dans la liste b au sein de la fonction de rappel onAct() et sera finalement considérée comme la liste actuelle. La population est initialisée en choisissant au hasard 1000 cellules initialement vivantes dans la fonction de rappel onReset() qui est appelée lors d’un clic sur le bouton « reset ». from gamegrid import * def onReset(): for x in range(s): for y in range(s): a[x][y] = 0 # All cells dead for n in range(z): loc = getRandomEmptyLocation() a[loc.x][loc.y] = 1 showPopulation() def showPopulation(): for x in range(s): for y in range(s): loc = Location(x, y) if a[x][y] == 1: getBg().fillCell(loc, Color.green, False) else: getBg().fillCell(loc, Color.black, False) refresh() def getNumberOfNeighbours(x, y): nb = 0 for i in range(max(0, x - 1), min(s, x + 2)): for k in range(max(0, y - 1), min(s, y + 2)): if not (i == x and k == y): if a[i][k] == 1: nb = nb + 1 return nb def onAct(): global a # Don't use the current, but a new population b = [[0 for x in range(s)] for y in range(s)] for x in range(s): for y in range(s): nb = getNumberOfNeighbours(x, y) if a[x][y] == 1: # living cell if nb < 2: b[x][y] = 0 elif nb > 3: b[x][y] = 0 else: b[x][y] = 1 else: # dead cell if nb == 3: b[x][y] = 1 else: b[x][y] = 0 a = b # Use new population as current showPopulation() # =================== global section ================== s = 50 # Number of cells in each direction z = 1000 # Size of population at start a = [[0 for x in range(s)] for y in range(s)] makeGameGrid(s, s, 800 // s, Color.red) registerAct(onAct) registerNavigation(resetted = onReset) setTitle("Conway's Game Of Life") onReset() show() |
MEMENTO |
Le jeu de la vie est un exemple typique d’automate cellulaire constitué de cellules d’une grille en interaction les unes avec les autres. Les automates cellulaires se prêtent très bien à l’étude du comportement de systèmes naturels complexes parmi lesquels on trouve
En 2002, Stefan Wolfram, le scientifique et développeur en chef de Mathematica fit remarquer, dans son fameux livre "A New Kind of Science", que de tels systèmes peuvent être étudiés à l’aide de programmes simples. Les simulations informatiques nous placent à la veille d’une nouvelle ère dans la manière d’acquérir des connaissances scientifiques. Pour initialiser une liste à deux dimensions (liste de listes), on utilise une syntaxe python spéciale appelée compréhension de liste (list comprehensionen anglais) (voir Matériel supplémentaire). |
COMPORTEMENT EN ESSAIM |
Comme vous avez déjà pu l’observer souvent dans la vie, de nombreux êtres vivants ont tendance à former de grands groupes d’individus. Ce phénomène est particulièrement évident chez les oiseaux, les poissons et les insectes. Un groupe de personnes réunies pour une manifestation présentent également une forme de « comportement grégaire ». La formation d’un essaim d’individus est influencée d’une part par des facteurs extérieurs globaux et d’autre part par les interactions des partenaires dans leur environnement immédiat (influences locales). En 1986, Craig Reynolds a démontré que la formation d’un essaim d’individus qu’il appela Boids est régie par les trois règles suivantes:
Afin d’implémenter ce comportement, on utilise à nouveau JGameGrid afin de minimiser les ressources nécessaires pour effectuer le rendu de l’animation. Il est alors possible d’utiliser une grille de jeu dont les cellules se réduisent à un pixel et de spécifier la position, la vitesse et l’accélération des acteurs à l’aide de vecteurs en virgule flottante de la classe GGVector. À chaque période de simulation, on commence par déterminer le nouveau vecteur accélération à partir des trois règles de formation d’essaim grâce à la fonction setAcceleration(). On obtient ainsi les nouveaux vecteurs vitesse et position
Puisque l’échelle de temps absolu n’est pas essentielle, on peut sans autre fixer l’incrément temporel à dt = 1. L’application de la règle de séparation conduit non seulement à une répulsion entre les oiseaux trop rapprochés, mais également un évitement des obstacles, en l’occurrence les arbres. Il faut faire particulièrement attention à bien gérer les limites de la zone de vol (les côtés du canevas). On peut imaginer plusieurs possibilités. On pourrait, par exemple, utiliser une topologie toroïdale dans laquelle les oiseaux quittant la zone de vol d’un côté réapparaissent automatiquement de l’autre. Dans le programme suivant, on a simplement fait le choix d’imposer aux oiseaux de faire demi-tour lorsqu’ils parviennent aux bords. from gamegrid import * import math from random import randint # =================== class Tree ======================= class Tree(Actor): def __init__(self): Actor.__init__(self, "sprites/tree1.png") # =================== class Bird ======================= class Bird(Actor): def __init__(self): Actor.__init__(self, True, "sprites/arrow1.png") self.r = GGVector(0, 0) # Position self.v = GGVector(0, 0) # Velocity self.a = GGVector(0, 0) # Acceleration # Called when actor is added to gamegrid def reset(self): self.r.x = self.getX() self.r.y = self.getY() self.v.x = startVelocity * math.cos(math.radians(self.getDirection())) self.v.y = startVelocity * math.sin(math.radians(self.getDirection())) # ----------- cohesion --------------- def cohesion(self, distance): return self.getCenterOfMass(distance).sub(self.r) # ----------- alignment -------------- def alignment(self, distance): align = self.getAverageVelocity(distance) align = align.sub(self.v) return align # ----------- separation ------------- def separation(self, distance): repulse = GGVector() # ------ from birds ------ for p in birdPositions: dist = p.sub(self.r) d = dist.magnitude() if d < distance and d != 0: repulse = repulse.add(dist.mult((d - distance) / d)) # ------ from trees ------ trees = self.gameGrid.getActors(Tree) for actor in trees: p = GGVector(actor.getX(), actor.getY()) dist = p.sub(self.r) d = dist.magnitude() if d < distance and d != 0: repulse = repulse.add(dist.mult((d - distance) / d)) return repulse # ----------- wall interaction ------- def wallInteraction(self): width = self.gameGrid.getWidth() height = self.gameGrid.getHeight() acc = GGVector() if self.r.x < wallDist: distFactor = (wallDist - self.r.x) / wallDist acc = GGVector(wallWeight * distFactor, 0) if width - self.r.x < wallDist: distFactor = ((width - self.r.x) - wallDist) / wallDist acc = GGVector(wallWeight * distFactor, 0) if self.r.y < wallDist: distFactor = (wallDist - self.r.y) / wallDist acc = GGVector(0, wallWeight * distFactor) if height - self.r.y < wallDist: distFactor = ((height - self.r.y) - wallDist) / wallDist acc = GGVector(0, wallWeight * distFactor) return acc def getPosition(self): return self.r def getVelocity(self): return self.v def getCenterOfMass(self, distance): center = GGVector() count = 0 for p in birdPositions: dist = p.sub(self.r) d = dist.magnitude() if d < distance: center = center.add(p) count += 1 if count != 0: return center.mult(1.0/count) else: return center def getAverageVelocity(self, distance): avg = GGVector() count = 0 for i in range(len(birdPositions)): p = birdPositions[i] if (self.r.x - p.x) * (self.r.x - p.x) + \ (self.r.y - p.y) * (self.r.y - p.y) < distance * distance: avg = avg.add(birdVelocities[i]); count += 1 return avg.mult(1.0/count) def limitSpeed(self): m = self.v.magnitude() if m < minSpeed: self.v = self.v.mult(minSpeed / m) if m > maxSpeed: self.v = self.v.mult(minSpeed / m) def setAcceleration(self): self.a = self.cohesion(cohesionDist).mult(cohesionWeight) self.a = self.a.add(self.separation(separationDist).mult(separationWeight)) self.a = self.a.add(self.alignment(alignmentDist).mult(alignmentWeight)) self.a = self.a.add(self.wallInteraction()) def act(self): self.setAcceleration() self.v = self.v.add(self.a) # new velocity self.limitSpeed() self.r = self.r.add(self.v) # new position self.setDirection(int(math.degrees(self.v.getDirection()))) self.setLocation(Location(int(self.r.x), int(self.r.y))) # =================== global section ================== def populateTrees(number): blockSize = 70 treesPerBlock = 10 for block in range(number // treesPerBlock): x = getRandomNumber(800 // blockSize) * blockSize y = getRandomNumber(600 // blockSize) * blockSize for t in range(treesPerBlock): dx = getRandomNumber(blockSize) dy = getRandomNumber(blockSize) addActor(Tree(), Location(x + dx, y + dy)) def generateBirds(number): for i in range(number): addActorNoRefresh(Bird(), getRandomLocation(), getRandomDirection()) onAct() # Initialize birdPositions, birdVelocities def onAct(): global birdPositions, birdVelocities # Update bird positions and velocities birdPositions = [] birdVelocities = [] for b in getActors(Bird): birdPositions.append(b.getPosition()) birdVelocities.append(b.getVelocity()) def getRandomNumber(limit): return randint(0, limit-1) # coupling constants cohesionDist = 100 cohesionWeight = 0.01 alignmentDist = 30 alignmentWeight = 1 separationDist = 30 separationWeight = 0.2 wallDist = 20 wallWeight = 2 maxSpeed = 20 minSpeed = 10 startVelocity = 10 numberTrees = 100 numberBirds = 50 birdPositions = [] birdVelocities = [] makeGameGrid(800, 600, 1, False) registerAct(onAct) setSimulationPeriod(10) setBgColor(makeColor(25, 121, 212)) setTitle("Swarm Simulation") show() populateTrees(numberTrees) generateBirds(numberBirds) doRun() |
MEMENTO |
La simulation dépend d’un certain nombre de constantes de couplage qui déterminent l’intensité de l’interaction entre les individus. Ces valeurs sont très sensibles et il pourrait être nécessaire de les ajuster en fonction de la puissance de traitement de votre ordinateur. Encore une fois, la fonction de rappel onAct() est activée en utilisant registerAct() de sorte qu’elle est appelée automatiquement à chaque cycle de simulation. Le mouvement des oiseaux est géré par la méthode act() de la classe Bird. |
EXERCICES |
|
MATÉRIEL SUPPLÉMENTAIRE |
COMPRÉHENSION DE LISTE |
|
En Python, il est possible de créer des listes de manière très élégante en utilisation une syntaxe spéciale inspirée de la notation de la théorie des ensembles que vous connaissez bien des mathématiques :
N’hésitez pas à utiliser la console pour tester les expressions Python. Pour ce faire, vous pouvez les copier depuis le tableau ci-dessous et les coller dans la console:
|