8.4 TEMPS MOYEN D‘ATTENTE
![]()
INTRODUCTION |
|
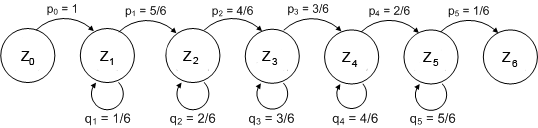
De nombreux systèmes présentent un comportement temporel qui peut être décrit par des transitions d’un état à l’autre. La transition d’un état système Zi à un état suivant Zk est déterminée par la probabilité pik. Dans l’exemple suivant, on jette un dé et l’on considère le nombre de faces du dé différentes déjà survenues comme une variable d’état: Z0: Encore aucun jet effectué On peut illustrer la transition entre les états dans le schéma suivant o chaîne de Markov
Les probabilités sont interprétées de la manière suivante : si l’on a déjà obtenu n faces différentes, la probabilité d’obtenir à nouveau une de ces faces vaut n/6 tandis que la probabilité d’obtenir une face encore jamais survenue vaut (6-n)/6. Vous pouvez essayer de déterminer combien de fois il faut relancer le dé en moyenne pour que toutes les faces apparaissent au moins une fois.
|
TEMPS MOYEN D’ATTENTE |
Si l’on jette le dé à intervalles de temps réguliers, la question précédente revient à déterminer le temps nécessaire pour que toutes les faces surviennent au moins une fois. On appelle ceci le temps moyen d’attente. On peut déterminer ce temps en faisant la réflexion suivante : le temps moyen pour passer de Z0 à Z6correspond à la somme des temps d’attente pour l’ensemble des transitions. Mais que vaut alors le temps d’attente de chaque transition individuelle? Notre premier programme met en évidence la propriété la plus essentielle des problèmes de temps d’attente: Si p est la probabilité de passer de Z1 à Z2le temps d’attente s’élève environ à u = 1/p (dans une unité appropriée).
from gpanel import * from random import randint n = 10000 p = 1/6 def sim(): k = 1 r = randint(1, 6) while r != 6: r = randint(1, 6) k += 1 return k makeGPanel(-5, 55, -200, 2200) drawGrid(0, 50, 0, 2000) title("Waiting on a 6") h = [0] * 51 lineWidth(5) count = 0 repeat n: k = sim() count += k if k <= 50: h[k] += 1 line(k, 0, k, h[k]) mean_exp = count / n lineWidth(1) setColor("red") count = 0 for k in range(1, 1000): pk = (1 - p)**(k - 1) * p nk = n * pk count += nk * k if k <=50: line(k, 0, k, nk) mean_theory = count / n title("Experiment: " + str(mean_exp) + "Theory: " + str(mean_theory)) |
MEMENTO |
|
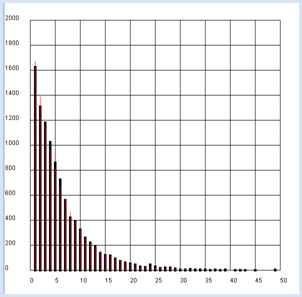
Le résultat est intuitivement évident : puisque la probabilité d’obtenir une des faces du dé vaut p=1/6, il faut en moyenne u = 1 / p = 6 jets pour obtenir cette face. Il est également instructif d’afficher la valeur théorique des fréquences comme une ligne rouge. Pour ce faire, il faut tenir compte des considérations suivantes en ce qui concerne la probabilité d’obtenir un 6:
Pour obtenir les fréquences théoriques, on multiplie ces probabilités par le nombre n d’essais [plus... Avec un peu d'algèbre, on peut montrer que l’espérance du temps d’attente qui est la somme des pk * k vaut exactement 1/p ]. |
PROGRAMMER AU LIEU DE CALCULER |
Pour résoudre le problème défini précédemment consistant à calculer le temps d’attente moyen jusqu’à ce que toutes les faces apparaissent au moins une fois, on décide d’adopter l’approche théorique. On interprète le processus comme une chaîne de Markov et l’on ajoute les temps d’attente de chaque transition individuelle: u = 1 + 6/5 + 6/4 + 6/3 + 6/2 + 6 = 14.7 On pourrait aussi adopter une approche empirique consistant à écrire un simple programme permettant de déterminer ce nombre à l’aide d’une simulation. Pour ce faire, on procède toujours de la même manière : on définit une fonction sim() dans laquelle l’ordinateur recherche une seule solution en utilisant les nombres aléatoires. Cette fonction retourne le nombre d’étapes nécessaires. On répète ensuite cette tâche de nombreuses fois, disons 1'000 fois, et l’on détermine la valeur moyenne. La fonction sim() utilise une liste z dans laquelle on insère les faces qui ne s’y trouvent pas déjà. Dès que cette liste possède six éléments, on sait que toutes les faces du dé sont survenues. from random import randint n = 10000 def sim(): z = [] i = 0 while True: r = randint(1, 6) i += 1 if not r in z: z.append(r) if len(z) == 6: return i count = 0 repeat n: count += sim() print("Mean waiting time:", count / n) |
MEMENTO |
La simulation informatique livre la valeur 14,68 qui fluctue légèrement d’une fois à l’autre mais qui correspond à la prédiction théorique. On remarque donc que l’ordinateur peut être utilisé pour vérifier rapidement l’exactitude d’un résultat théorique. Cependant, la détermination théorique du temps d’attente peut devenir très complexe pour des problèmes pourtant relativement simples. Si, par exemple, on essaie de déterminer le temps moyen d’attente jusqu’à l’obtention d’une certaine somme des nombres, le problème est extrêmement simple à résoudre à l’aide d’une simulation informatique. from random import randint n = 10000 s = 7 # rolled count of the die numbers def sim(): i = 0 total = 0 while True: i += 1 r = randint(1, 6) total += r if total >= s: break return i count = 0 repeat n: count += sim() print("Mean waiting time:", count / n) |
MEMENTO |
On obtient un temps moyen d’attente d’environ 2.52 jets pour obtenir une somme de 7. Ce résultat est assez surprenant puisque l’espérance pour chaque jet vaut 3.5. De ce fait, on peut admettre qu’il faut lancer le dé en moyenne deux fois pour obtenir une somme de points supérieure ou égale à 7. Le calcul théorique, au contraire de la simulation, peut facilement prendre des heures. Voici le résultat théorique : 117 577 / 46'656 = 2.5008. De ce fait, même les mathématiciens utilisent l’ordinateur pour éprouver rapidement un résultat théorique et vérifier leurs hypothèses. |
PROPAGATION D’UNE MALADIE |
Bien qu’elle soit fictive, admettons l’histoire suivante puisqu’elle comporte certains parallèles avec le vécu réel de certaines communautés d’êtres vivants:
Une bonne façon de représenter cette situation consiste à travailler avec une liste de valeurs booléennes où le caractère « en bonne santé » est codé par False et « malade » est codé par True. L’avantage de cette structure de données réside dans le fait qu’au sein de la fonction pair(), l’interaction entre deux personnes peut simplement être réalisée à l’aide de la fonction logique OU (or):
from gpanel import * from random import randint def pair(): # Select two distinct inhabitants a = randint(0, 99) b = a while b == a: b = randint(0, 99) z[a] = z[a] or z[b] z[b] = z[a] def nbInfected(): count = 0 for i in range(100): if z[i]: count += 1 return count makeGPanel(-50, 550, -10, 110) title("The spread of an illness") drawGrid(0, 500, 0, 100) lineWidth(2) setColor("blue") z = [False] * 100 tmax = 500 t = 0 a = randint(0, 99) z[a] = True # random infected inhabitant move(t, 1) while t <= tmax: pair() infects = nbInfected() t += 1 draw(t, infects) |
MEMENTO |
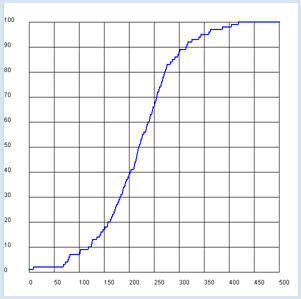
On observe un comportement temporel dans lequel la propagation de la maladie est lente au début, puis rapide, puis à nouveau lente. Ce comportement s’explique par le fait qu’au début, la probabilité qu’une personne malade rencontre une personne en bonne santé est relativement faible. Par la suite, puisque de nombreuses personnes sont malades, cette probabilité augmente fortement ce qui produit une propagation rapide de la maladie. Dans la dernière phase, comme il n’y a presque plus que des personnes malades, la probabilité qu’une personne saine et une personne malade se rencontrent devient à nouveau faible. [plus... Ce processus correspond tendanciellement à la croissance logistique d’une population]. |
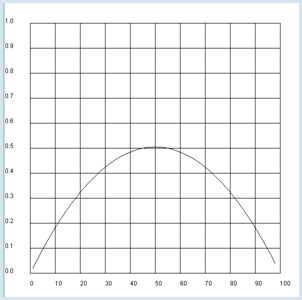
from random import randint n = 1000 # number experiment def pair(): # Select two distinct inhabitants a = randint(0, 99) b = a while b == a: b = randint(0, 99) z[a] = z[a] or z[b] z[b] = z[a] def nbInfected(): count = 0 for i in range(100): if z[i]: count += 1 return count def sim(): global z z = [False] * 100 t = 0 a = randint(0, 99) z[a] = True # random infected inhabitant while True: pair() t += 1 if nbInfected() == 100: return t count = 0 for i in range(n): u = sim() print("Experiment #", i + 1, "Waiting time:", u) count += u print( "Mean waiting time:", count / n) On peut également illustrer la propagation de la maladie à l’aide d’une chaîne de Markov. Un état donné de la chaîne de Markov est caractérisé par le nombre de personnes infectées. Pour une population de 100 personnes, le temps nécessaire pour que tout le monde tombe malade correspond à la somme des temps d’attente pour chaque transition de k à k+1 personnes malades, pour k allant de 1 à 99. De plus, pour réaliser cette simulation, il est nécessaire de connaître la probabilité de transition pk.
from gpanel import * n = 100 def p(k): return 2 * k * (n - k) / n / (n - 1) makeGPanel(-10, 110, -0.1, 1.1) drawGrid(0, 100, 0, 1.0) count = 0 for k in range(1, n - 1): if k == 1: move(k, p(k)) else: draw(k, p(k)) count += 1 / p(k) title("Time until everyone is ill: " + str(count)) |
MEMENTO |
En utilisant la théorie des chaines de Markov, on obtient donc un temps d’attente moyen de 463 heures jusqu’à ce que toutes les personnes de l’île soient infectées, ce qui correspond à environ 20 jours. |
RECHERCHE DE PARTENAIRE À L’AIDE D’UN PROGRAMME |
Une question intéressante en pratique concerne la stratégie optimale de recherche d’un partenaire de vie. On fait en l’occurrence l’hypothèse que cent partenaires possèdent des niveaux de qualification croissants. Ils seront présentés dans un ordre aléatoire et, dans une phase d’apprentissage, on a la possibilité de les ordonner correctement par niveau croissant de compétences en se basant sur les évaluations précédentes. Cependant, on ne connait pas le niveau de compétence maximal. Lors de chaque présentation, on doit décider si l’on accepte ou si l’on rejette le partenaire. Quelle est la meilleure stratégie pour s’assurer de choisir le meilleur partenaire avec une grande probabilité? Pour cette simulation, on crée dans la fonction sim(x) une liste t de 100 niveaux de compétences de 0 à 99 ordonnés aléatoirement à l’aide de la fonction shuffle().
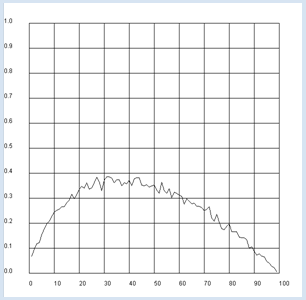
from random import shuffle from gpanel import * n = 1000 # Number of simulations a = 100 # Number of partners def sim(x): # Random permutation [0..99] t = [0] * 100 for i in range(0, 100): t[i] = i shuffle(t) best = max(t[0:x]) for i in range(x, 100): if t[i] > best: return [i, t[i]] return [99, t[99]] makeGPanel(-10, 110, -0.1, 1.1) title("The probability of finding the best partner from 100") drawGrid(0, 100, 0, 1.0) for x in range(1, 100): count = 0 repeat n: z = sim(x) if z[1] == 99: # best score count += 1 p = count / n if x == 1: move(x, p) else: draw(x, p)
|
MEMENTO |
Apparemment, on a les meilleures chances de choisir le meilleur partenaire après une phase d’apprentissage de longueur 37 [plus... La valeur théorique est donnée par 100 / e]. |
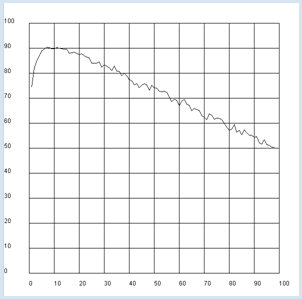
from random import shuffle from gpanel import * n = 1000 # Number of simulations def sim(x): # Random permutation [0..99] t = [0] * 100 for i in range(0, 100): t[i] = i shuffle(t) best = max(t[0:x]) for i in range(x, 100): if t[i] > best: return [i, t[i]] return [99, t[99]] makeGPanel(-10, 110, -10, 110) title("Mean qualification after waiting for a partner") drawGrid(0, 100, 0, 100) for x in range(1, 99): count = 0 repeat n: u = sim(x) count += u[1] y = count / n if x == 1: move(x, y) else: draw(x, y) |
MEMENTO |
Ce deuxième critère d’optimalité livre un résultat complètement différent : il faut choisir le prochain partenaire ayant les meilleures compétences déjà après une phase d’apprentissage d’environ 10 présentations. On peut également effectuer la simulation pour un nombre de partenaires plus réaliste et observer que la phase d’apprentissage optimale demeure relativement courte. |
PARADOXE DU TEMPS D’ATTENTE |
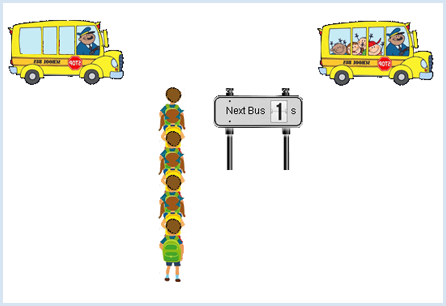
Puisque les transports arrivent également toutes les 6 minutes en moyenne dans cette situation, on pourrait croire que le temps d’attente moyen est également de 3 minutes. Le résultat surprenant, et donc paradoxal, est que le temps d’attente est dans ce cas supérieure à 3 minutes. Pour s’en convaincre, on utilise une simulation animée permettant de déterminer le temps moyen d’attente sous l’hypothèse que les bus arrivent à l’arrêt de bus espacés par un intervalle de temps uniformément distribué entre 2 et 10 minutes. Dans la simulation, les minutes seront des secondes pour accélérer le processus. On peut se servir de la bibliothèque de jeux JGameGrid puisqu’elle permet de modéliser facilement des objets tels que des bus et des passagers à l’aide de sprites.
Le code du programme requiert certainement quelques explications : Puisque l’on a affaire à des objets de type bus et passagers, ont modélise ceci à l’aide des classes Bus et Passenger. Les bus sont créés au sein d’une boucle infinie à la fin de la partie principale du programme en accord avec les implications statistiques de notre hypothèse. Lorsque la fenêtre graphique est fermée, la boucle infinie se termine puisque la méthode isDisposed() renvoie alors la valeur False, ce qui a pour effet de terminer le programme. Les passagers doivent être générés périodiquement et affichés dans la queue. Le meilleur moyen de réaliser ceci est de définir une classe PassengerFactory qui dérive de la classe Actor. Bien que cette dernière ne possède pas d’image de sprite, sa méthode act() peut être utilisées pour générer des passagers et les insérer dans la grille de jeu GameGrid. On peut changer la période avec laquelle les objets sont générés à l’aide du compteur de cycles nbCycles (le cycle de simulation est fixé à 50 ms). On fait avancer le bus à l’aide de la méthode act() de la classe Bus et on vérifie s’il est arrivé à l’arrêt à l’aide de ses coordonnées x. Lorsque le bus parvient à l’arrêt, on invoque la méthode board() de la classe PassengerFactory qui a pour effet de supprimer de la queue les passagers en attente. Simultanément, on change l’image de sprite du bus avec show(1) et l’on affiche le nouveau temps d’attente jusqu’à l’arrivée du prochain bus sur le panneau. On utilise la variable booléenne isBoarded pour garantir que ces actions ne soient effectuées qu’une seule fois. Le panneau (scoreboard), qui est une instance de la classe InformationPanel constitue un gadget supplémentaire permettant d’afficher le temps jusqu’à l’arrivée du prochain bus. L’écran du panneau d’affichage sera mis à jour dans la méthode act() en sélectionnant une des 10 images de sprite (digit_0.png à digit_9.png)grâce la fonction show(). from gamegrid import * from random import random, randint import time min_value = 2 max_value = 10 def random_t(): return min_value + (max_value - min_value) * random() # ---------------- class PassengerFactory ---------- class PassengerFactory(Actor): def __init__(self): self.nbPassenger = 0 def board(self): for passenger in getActors(Passenger): passenger.removeSelf() passenger.board() self.nbPassenger = 0 def act(self): if self.nbCycles % 10 == 0: passenger = Passenger( randint(0, 1)) addActor(passenger, Location(400, 120 + 27 * self.nbPassenger)) self.nbPassenger += 1 # ---------------- class Passenger ----------------- class Passenger(Actor): totalTime = 0 totalNumber = 0 def __init__(self, i): Actor.__init__(self, "sprites/pupil_" + str(i) + ".png") self.createTime = time.clock() def board(self): self.waitTime = time.clock() - self.createTime Passenger.totalTime += self.waitTime Passenger.totalNumber += 1 mean = Passenger.totalTime / Passenger.totalNumber setStatusText("Mean waiting time: " + str(round(mean, 2)) + " s") # ---------------- class Car ----------------------- class Bus(Actor): def __init__(self, lag): Actor.__init__(self, "sprites/car1.gif") self.lag = lag self.isBoarded = False def act(self): self.move() if self.getX() > 320 and not self.isBoarded: passengerFactory.board() self.isBoarded = True infoPanel.setWaitingTime(self.lag) if self.getX() > 1650: self.removeSelf() # ---------------- class InformationPanel ---------- class InformationPanel(Actor): def __init__(self, waitingTime): Actor.__init__(self, "sprites/digit.png", 10) self.waitingTime = waitingTime def setWaitingTime(self, waitingTime): self.waitingTime = waitingTime def act(self): self.show(int(self.waitingTime + 0.5)) if self.waitingTime > 0: self.waitingTime -= 0.1 periodic = askYesNo("Departures every 6 s?") makeGameGrid(800, 600, 1, None, None, False) addStatusBar(20) setStatusText("Acquiring data...") setBgColor(Color.white) setSimulationPeriod(50) show() doRun() if periodic: setTitle("Warting Time Paradoxon - Departure every 6 s") else: setTitle("Waiting Time Paradoxon - Departure between 2 s and 10 s") passengerFactory = PassengerFactory() addActor(passengerFactory, Location(0, 0)) addActor(Actor("sprites/panel.png"), Location(500, 120)) addActor(TextActor("Next Bus"), Location(460, 110)) addActor(TextActor("s"), Location(540, 110)) infoPanel = InformationPanel(4) infoPanel.setSlowDown(2) addActor(infoPanel, Location(525, 110)) while not isDisposed(): if periodic: lag = 6 else: lag = random_t() bus = Bus(lag) addActor(bus, Location(-100, 40)) a = time.clock() while time.clock() - a < lag and not isDisposed(): delay(10)
|
MEMENTO |
La simulation montre bien que le temps moyen d’attente se situe aux alentours de 3.5 minutes, ce qui est clairement plus long que les 3 minutes d’attente nécessaires dans le cas où les bus sont tous espacés de 6 minutes exactement. On peut expliquer cette différence de la manière suivante : il est bien plus probable d’arriver à l’arrêt de bus lorsque le panneau affiche un temps d’attente compris entre 2 et 10 minutes que lorsqu’il affiche un temps compris entre 0 et 2 minutes. De ce fait, on a de fortes chances d’attendre plus que 3 minutes. |
EXERCICES |
|