8.5 SUITES ET CONVERGENCE
![]()
INTRODUCTION |
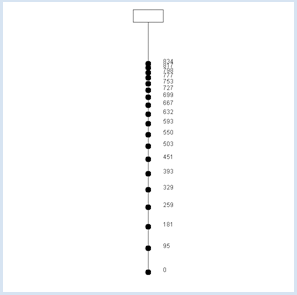
Les suites de nombres passionnent l’humanité depuis la nuit des temps. Dans l’Antiquité déjà, aux alentours de 200 avant J.C., Archimède était parvenu à approximer la valeur du nombre Pi. Il utilisa une suite de nombres correspondant au périmètre de polygones réguliers à n côtés inscrits dans un cercle de rayon r fixe, en prenant un nombre n de côtés toujours plus grand. Il lui est apparu clairement qu’il était fructueux de concevoir le cercle comme un cas limite de polygone possédant un nombre « infini » de côtés. Il en a conclu que la suite des périmètres de ces cercles tendait vers le périmètre du cercle inscrit. Une suite de nombres est constituée des nombres a0, a1, a2, etc.,à savoir des termes an d’indices n = 0, 1, 2, etc. (les suites commencent parfois à n = 1). Une règle de formation détermine clairement de manière unique la valeur de chacun des termes. Si ak est déterminé pour n’importe quel nombre naturel k aussi grand que l’on veut, on dit que la suite est infinie. Les termes de la suite peuvent être déterminés à l’aide d’une formule explicite dépendant de n. Cependant, le terme de rang n peut également être calculé à partir des termes précédents à l’aide d’une formule de récurrence. Dans ce cas, il est également nécessaire de connaitre la valeur des termes de départ. Une suite convergente possède une propriété très particulière : il existe un unique nombre g appelé limite vers lequel tendent les termes de la suite. Cela veut dire que l’on peut choisir un voisinage aussi petit que l’on veut autour de la limite g de sorte qu’à partir d’un rang n de la suite, aucun terme suivant ne se trouvera en dehors de ce voisinage. On peut se représenter ce voisinage comme une maison aux alentours de la limite : avant ce n donné, les termes peuvent osciller autour de la maison (le voisinage) mais à partir d’un certain rang n, tous les termes de la suite se trouvent à l’intérieur de cette maison, aussi petite soit-elle. 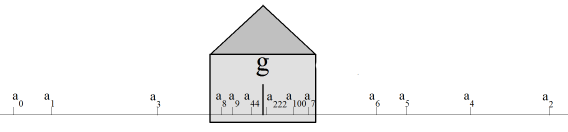 Il est possible d’étudier les suites de nombres de manière expérimentale à l’aide de l’ordinateur. On peut les représenter graphiquement de différentes manières : on peut, à la manière de l’illustration ci-dessus, représenter tous les termes de la suite comme des points ou des petits traits et déterminer s’il elle converge vers un point limite. Il est également possible d’étudier le comportement de la suite pour de grandes valeurs de n en la représentant dans un graphique à deux dimensions où n se trouve sur l’axe horizontal et les termes an sur l’axe vertical.
|
LE CHASSEUR ET SON CHIEN |
Un chasseur marche avec son chien en direction de leur pavillon de chasse situé à une distance d = 1000 m à une vitesse de 1 m/s. Comme le chien court plus vite que son maître, ils se déplacent de la manière suivante : le chien court seul à une vitesse u = 20 m/s en direction du pavillon de chasse, y fait demi-tour et s’en retourne vers son maître à la même vitesse. Dès qu’il atteint son maître, il fait à nouveau demi-tour et cours à nouveau en direction du pavillon de chasse. Il poursuit ce comportement jusqu’à ce que les deux aient atteint le pavillon de chasse.
On peut facilement en déduire la relation suivante avec des connaissances d’algèbre limitées:
Comme vous vous y attendiez certainement, les nombres an s’empilent jusqu’à atteindre le nombre limite 1000. from gpanel import * u = 1 # m/s v = 20 # m/s d = 1000 # m a = 0 # hunter h = 0 # dog c = 2 * u / (u + v) it = 0 makeGPanel(-50, 50, -100, 1100) title("Hunter-Dog problem") line(0, 0, 0, 1000) line(-5, 1000, 5, 1000) line(-5, 1050, 5, 1050) line(-5, 1000, -5, 1050) line(5, 1000, 5, 1050) while not isDisposed(): move(0, a) fillCircle(1) text(5, a, str(int(a))) getKeyWait() da = c * (d - a) dh = 2 * (d - a) - da h += dh a += da it += 1 title("it = " + str(it) + "; hunter = " + str(a) + " m; dog = " + str(h) + " m")
|
MEMENTO |
|
On dit que la suite de nombres an converge et que sa valeur limite est 1000. Essayez de saisir la nature purement théorique de cette formulation du problème. Elle correspond à l’anecdote antique rapportant que Achille fut invité à faire la course avec une tortue en lui laissant 10 mètres d’avance puisqu’il courait 10 fois plus vite qu’elle. On raconte qu’Achille refusa la compétition car, selon lui, il n’avait aucune chance de la rattraper. Son argument était le suivant : pendant qu’il parcourrait les 10 premiers mètres, la tortue aurait avancé d’un mètre et se trouverait donc au onzième mètre. Pendant qu’il parcourrait le mètre suivant, la tortue aurait parcouru encore 10 cm et se trouverait donc à 11,1 m du départ. Pendant qu’il parcourrait les 10 centimètres suivants, la tortue aurait parcouru encore 1 cm et se trouverait donc à 11,11 m du départ et ainsi de suite. Que pensez-vous de ce raisonnement ? |
DIAGRAMME DE BIFURCATION DE FEIGENBAUM |
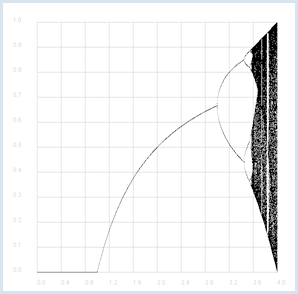
Nous avons déjà étudié la croissance logistique dans le cadre de la dynamique des populations. La taille de la population xnew dans la génération suivante est calculée à partir de sa taille actuelle x à l’aide d’une relation quadratique. Dans la suite, cette relation sera simplifiée par la relation
où le paramètre r peut être choisi arbitrairement. On voudrait savoir si la suite de nombres récursive
an+1 = r * an * (1 - an)
from gpanel import * def f(x, r): return r * x * (1 - x) makeGPanel(-0.6, 4.4, -0.1, 1.1) title("Tree Diagram") drawGrid(0, 4.0, 0, 1.0, "gray") for z in range(1001): r = 4 * z / 1000 a = 0.5 for i in range(1001): a = f(a, r) if i > 500: point(r, a)
|
MEMENTO |
|
Dans cette expérience, on met en évidence les points d’accumulation de la suite pour un certain r donné. Sur la base de cette simulation informatique, on peut établir les hypothèses suivantes : pour r < 1 il y a un point d’accumulation en zéro et la suite converge vers 0. Pour des valeurs de r comprises entre 1 et 3, la suite converge également. Pour des valeurs de r encore plus grandes, il y a d’abord deux puis plusieurs points d’accumulation. À partir d’une certaine valeur de r, la suite saute dans tous les sens de manière chaotique. |
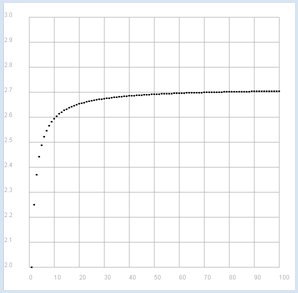
LE NOMBRE D’EULER |
from gpanel import * def a(n): return (1 + 1/n)**n makeGPanel(-10, 110, 1.9, 3.1) title("Euler Number") drawGrid(0, 100, 2.0, 3.0, "gray") for n in range(1, 101): move(n, a(n)) fillCircle(0.5)
|
MEMENTO |
Il s’agit du nombre d’Euler, l’un des nombres les plus célèbres. |
SUITES RAPIDEMENT CONVERGENTES POUR LE CALCUL DE PI |
Le calcul d’un nombre quelconque de décimales de π a toujours constitué un défi pour les mathématiciens. Ce n’est qu’en 1995 que les mathématiciens Bailey, Borwein et Plouffe ont prouvé la formule BBP sous forme de somme permettant ce calcul. Ils ont montré que l’on peut obtenir exactement le nombre π comme limite d’une suite dont le terme de rang n est donné par la somme des
pour k allant de 0 à n. Le programme suivant utilise le module decimal qui permet de calculer avec des nombres décimaux avec une très grande précision. Le constructeur de cette classe crée un tel nombre à partir d’un entier ou d’en flottant et autorise les opérations arithmétiques habituelles de manière transparente. La précision du calcul peut être réglée à l’aide de getcontext().prec et correspond en gros au nombre de décimales significatives. À chaque pression d’une touche du clavier, le programme calcule le prochain terme de la suite qu’il affiche ensuite dans une boîte de dialogue EntryDialog.
from entrydialog import * from decimal import * getcontext().prec = 50 def a(k): return 1/16**Decimal(k) * (4 / (8 * Decimal(k) + 1) - 2 / (8 * Decimal(k) + 4) - 1 / (8 * Decimal(k) + 5) - 1 / (8 * Decimal(k) + 6)) inp = IntEntry("n", 0) out = StringEntry("Pi") pane0 = EntryPane(inp, out) btn = ButtonEntry("Next") pane1 = EntryPane(btn) dlg = EntryDialog(pane0, pane1) dlg.setTitle("BBP Series - Click Next") n = 0 s = a(0) out.setValue(str(s)) while not dlg.isDisposed(): if btn.isTouched(): n = inp.getValue() if n == None: out.setValue("Illegal entry") else: n += 1 s += a(n) inp.setValue(n) out.setValue(str(s))
|
MEMENTO |
|
Après 40 itérations, la valeur de π affichée ne change plus. Le programme se termine lorsque l’on ferme la fenêtre puisque isDisposed() est True. |
EXERCICES |
|
MATÉRIEL SUPPLÉMENTAIRE |
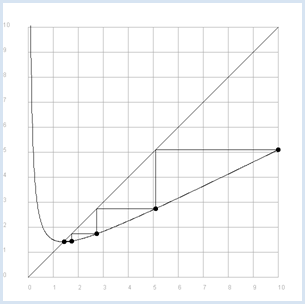
RÉSOLUTION ITÉRATIVE D’UNE ÉQUATION |
from gpanel import * def f(x): return 1 / 2 * (x + 2 / x) makeGPanel(-1, 11, -1, 11) title("Iterative square root begins at x = 10. Press a key...") drawGrid(0, 10, 0, 10, "gray") for i in range(10, 1001): x = 10 / 1000 * i if i == 10: move(x, f(x)) else: draw(x, f(x)) line(0, 0, 10, 10) x = 10 move(x, f(x)) fillCircle(0.1) it = 0 while not isDisposed(): getKeyWait() it += 1 xnew = f(x) line(x, f(x), xnew, f(x)) line(xnew, f(x), xnew, f(xnew)) x = xnew move(x, f(x)) fillCircle(0.1) title("Iteration " + str(it) + ": x = " + str(x))
|
MEMENTO |
Cette expérience montre clairement qu’en seulement quelques itérations (pression sur une touche du clavier), les points convergent très rapidement vers le point d’intersection, ce qui permet d’obtenir très rapidement une précision de 10 décimales. |