EINFÜHRUNG

Will man untersuchen, welche Probleme ein Computer grundsätzlich lösen kann und welches seine Grenzen sind, so muss man zuerst exakt definieren, was man unter einer Rechenmaschine versteht. Der berühmte Mathematiker und Informatiker Alan Turing veröffentlichte bereits 1936 eine Untersuchung zu diesem Thema, lange bevor es überhaupt einen programmierbaren Digitalrechner gab. Die nach ihm benannte Turingmaschine durchläuft programmgesteuert und auf Grund von Eingabewerten, die sie von einem Band liest, schrittweise einzelne Zustände und schreibt dabei Ausgabewerte auf das Band. Diese grundsätzliche Vorstellung über die Funktionsweise des Computers ist auch heute noch gültig, denn jeder Prozessor ist eigentlich eine Turingmaschine, die im Takt einer Clock Zustand um Zustand durchläuft. Besser an die Praxis angepasst sind allerdings Zustandsautomaten, die sich mit Zustandsgraphen modellieren lassen. Man nennt sie Endliche Automaten.

DIE ESPRESSO-MASCHINE ALS MEALY-AUTOMAT

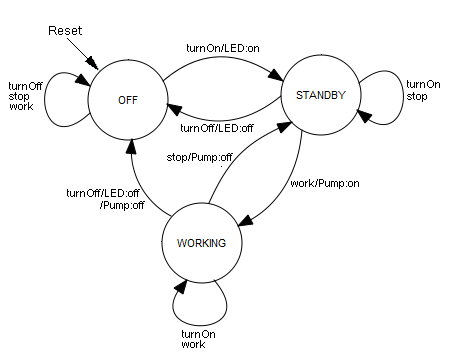
Im täglichen Leben machst du Bekanntschaft mit vielen Geräten und Maschinen, die du als Automaten auffassen kannst. Dazu gehören Getränkeautomaten, Waschautomaten, Geldautomaten, usw. Als Ingenieur und Informatiker entwickelst du einen solchen Automaten mit der klaren Vorstellung, dass dieser ausgehend von einem aktuellen Zustand schrittweise in einen Nachfolgezustand übergeht, der von Sensordaten und der Betätigung von Tasten und Schaltern abhängt. Dies nennst du die Eingaben des Automaten. Bei jedem Übergang betätigt der Automat bestimmte Aktoren, wie Motoren, Pumpen, Lampen usw. Dies nennst du die Ausgaben des Automaten.

Du entwickelst hier einen Espresso-Automaten, der 3 Zustände besitzt: Er kann ausgeschaltet (OFF), betriebsbereit (STANDBY) und am Kaffeepumpen (WORKING) sein. Zur Bedienung stehen 4 Drucktasten für die Funktionen Einschalten (turnOn), Ausschalten (turnOff), Kaffeepumpe einschalten (work), Kaffeepumpe ausschalten (stop) zur Verfügung.

Du kannst zwar die Funktionsweise des Espresso-Automaten in Worten beschreiben. Viel anschaulicher ist es aber, den Automatengraph zu zeichnen. Dabei stellst du die Zustände mit einem Kreis und die Übergänge als Übergangspfeile dar, die du mit den Eingaben/Ausgaben anschreibst. Zudem ist es wichtig festzulegen, in welchem Anfangszustand der Automat ist, wenn du ihn ans Netz anschliesst. Da in jedem Zustand irgendeine Taste gedrückt werden kann, müssen bei jedem Zustand alle möglichen Eingaben vorkommen. Falls keine Aktion erfolgt, wird die Ausgabe weggelassen.

Automatengraph:

Du kannst das Verhalten auch in einer Tabelle festhalten, in der du zu jedem Zustand s und jeder Eingabe t den Nachfolgezustand s' angibst. Mit einem Stern bezeichnest du den Anfangszustand.

Übergangstabelle:

Mathematisch ausgedrückt kannst du sagen, dass der Nachfolgezustand s' eine Funktion des aktuellen Zustands s und der Eingabe t ist: s' = F(s, t). Du nennst F die Übergangsfunktion.

Die Ausgaben, die zu jedem Zustand und einer Eingabe gehören, kannst du ebenfalls tabellarisch festhalten:

Ausgabetabelle:

Mathematisch kannst du auch hier sagen, dass die Ausgabe g eine Funktion des aktuellen Zustands s und der Eingabe ist: g = G(s, t). Du nennst G die Ausgabefunktion.

MEMO

IMPLEMENTIERUNG DES ESPRESSO-AUTOMATEN MIT STRINGS

Der Auslöser für den Übergang von einem Zustand zum nächsten soll ein Tastendruck sein. Die betreffende Taste legt den Eingabewert fest, und zwar werden die 4 Cursor-Tasten verwendet. Die Implementierung ist typisch: In einer endlosen Ereignisschleife (event loop) wartet das Programm mit getEntry() auf eine Tastatureingabe. Mit dem Rückgabewert wird der aktuelle Zustand gemäss der Übergangstabelle geändert und die Ausgaben gemäss der Ausgabetabelle gemacht.

from gconsole import *

def getEntry():
    keyCode = getKeyCodeWait()
    if keyCode == 38: # up  
        return "stop"
    if keyCode == 40: # down
        return "work"
    if keyCode == 37: # left
        return "turnOff"
    if keyCode == 39: # right
        return "turnOn"
    return ""
    
state = "OFF"  # Start state
makeConsole()
while True:
    gprintln("State: " + state)
    entry = getEntry()
    if entry == "turnOff":
       if state == "STANDBY":
            state = "OFF"
            gprintln("LED off")
       if state == "WORKING":
            state = "OFF"
            gprintln("LED and pump off")
    elif entry == "turnOn":
        if state == "OFF":
            state = "STANDBY"
            gprintln("LED enabled")
    elif entry == "stop":
        if state == "WORKING":
            state = "STANDBY"
            gprintln("Pumpe off")
    elif entry == "work":
        if state == "STANDBY":
            state = "WORKING"
            gprintln("Pumpe enabled")

MEMO

ENUMERATIONEN ALS ZUSTANDS- UND EVENTBEZEICHNER

Da der Automat mit bestimmten Zuständen und bestimmten Eingabe- und Ausgabewerten arbeitet, ist es sinnvoll, dafür eine spezielle Datenstruktur einzuführen. Viele Programmiersprachen kennen dafür einen speziellen Aufzählungstyp (enumeration). In der Standardsyntax von Python fehlt dieser Datentyp leider, er wurde aber in TigerJython mit dem zusätzlichen Schlüsselwort enum()  hinzugefügt. Bei der Definition der Aufzählungswerte verwendet man Strings. Diese müssen sich an die erlaubte Namensgebung für Variablen halten.

from gconsole import *

def getEvent():
    keyCode = getKeyCodeWait()
    if keyCode == 38: # up  
        return Events.stop
    if keyCode == 40: # down
        return Events.work
    if keyCode == 37: # left
        return Events.turnOff
    if keyCode == 39: # right
        return Events.turnOn
    return None
    
State = enum("OFF", "STANDBY", "WORKING")
state = State.OFF
Events = enum("turnOn", "turnOff", "stop", "work")
makeConsole()
while True:
    gprintln("State: " + str(state))
    event = getEvent()
    if event == Events.turnOn:
        if state == State.OFF:
            state = State.STANDBY
    elif event == Events.turnOff:
            state = State.OFF
    elif event == Events.work:
        if state == State.STANDBY:
            state = State.WORKING
    elif event == Events.stop:
        if state == State.WORKING:
            state = State.STANDBY

MEMO

MAUSGESTEUERTE IMPLEMENTIERUNG DES ESPRESSO-AUTOMATEN

MEMO

DENKEN IN ZUSTÄNDEN / GRAFISCHE BENUTZEROBERFLÄCHE

Auf den ersten Blick scheinen Mealy-Automaten eine eher theoretische Angelegenheit zu sein. Dies ist aber keineswegs so. Vielmehr muss man bei modernen, eventgesteuerten Programmen mit einer grafischen Benutzeroberfläche immer in Zuständen denken. Als Beispiel schreibst du ein Turtle-Programm, das über 3 Buttons gesteuert wird:  Der Startbutton setzt die Turtle in Bewegung, der Stopbutton hält die Bewegung an und der Quitbutton beendet das Programm. Um das Programm richtig zu implementieren, musst du den Automatengraph im Kopf haben:

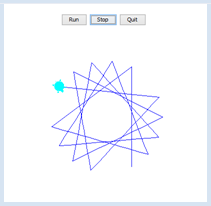
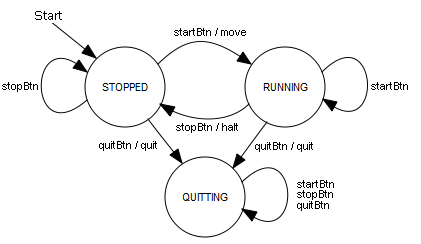
Wie du weisst, dürfen in Callbacks von GUI-Events keine Animationen und  nur kurz dauernder Code ausgeführt werden, da der Bildschirm nur am Ende der Funktion neu gerendert wird. Darum schaltest du in den Callbacks der Buttonklicks nur den Zustand um und führst die Bewegung der Turtle im Hauptteil des Programms aus.

Mehr zu diesem Problem erfährst du im Anhang 4: Parallelverarbeitung

from javax.swing import JButton
from gturtle import *

def buttonCallback(evt):
    global state
    source = evt.getSource()
    if source == runBtn:
        state = State.RUNNING
        setTitle("State: RUNNING")
    if source == stopBtn:
        state = State.STOPPED
        setTitle("State: STOPPED")
    if source == quitBtn:
        state = State.QUITTING
        setTitle("State: QUITTING")

State = enum("STOPPED", "RUNNING", "QUITTING")
state = State.STOPPED

runBtn = JButton("Run", actionPerformed = buttonCallback)
stopBtn = JButton("Stop", actionPerformed = buttonCallback)
quitBtn = JButton("Quit", actionPerformed = buttonCallback)
makeTurtle()
setTitle("State: STOPPED")
back(100)

pg = getPlayground()
pg.add(runBtn)
pg.add(stopBtn)
pg.add(quitBtn)
pg.validate()

while state != State.QUITTING and not isDisposed():
    if state == State.RUNNING:
          forward(200).left(127)
dispose()         

MEMO

AUFGABEN

ZUSATZSTOFF

AKZEPTOR FÜR REGULÄRE SPRACHEN

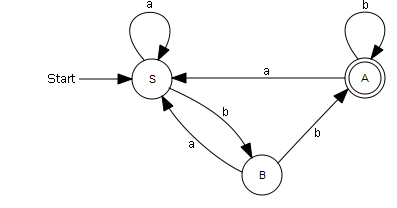
Eine formale Sprache besteht aus einem Alphabet von Zeichen und einem Regelsystem, mit dem man eindeutig entscheiden kann, ob eine bestimmte Zeichensequenz mit Zeichen aus diesem Alphabet zur Sprache gehört. Kann man das Regelsystem mit einem Automaten realisieren, so spricht man von einer regulären formalen Sprache.

Du betrachtest als Beispiel eine sehr einfache Sprache mit einem Alphabet, das nur aus den Buchstaben a und b besteht. Das Regelsystem kannst du als Spezialfall eines Mealy-Automaten auffassen, der keine Ausgabewerte erzeugt. Dabei liest der Automat ausgehend von einem Startzustand Zeichen um Zeichen und geht entsprechend des gelesenen Zeichens in einen Nachfolgezustand über. Befindet er sich nach dem Lesen des letzten Zeichens in einem der vorgegebenen Endzustände, so gehört das Wort zur Sprache. Du betrachtest den folgenden Automatengraphen (S: Startzustand, A: Endzustand):

In der Implementierung wird der Zustandswechsel durch Drücken der Buchstabentasten a oder b ausgelöst. Danach schreibt dein Programm den aktuellen Zustand und das bisher eingegebene Wort aus.

from gconsole import *

def getKeyEvent():
    global word
    keyCode = getKeyCodeWait(True)
    if keyCode == KeyEvent.VK_A:
        return Events.a
    if keyCode == KeyEvent.VK_B:
        return Events.b
    return None

State = enum("S", "A", "B")
state = State.S
Events = enum("a", "b")
makeConsole()
word = ""
gprintln("State: " + str(state))
while True:
    entry = getKeyEvent()
    if entry == Events.a:
        if state == State.A:
            state = State.S
        elif state == State.B:
            state = State.S
        word += "a"
        gprint("Word: " + word + " -> ")
        gprintln("State: " + str(state))
    elif entry == Events.b:
        if state == State.S:
            state = State.B
        elif state == State.B:
            state = State.A
        word += "b"
        gprint("Word: " + word + " -> ")
        gprintln("State: " + str(state))

MEMO

AUFGABEN