Forum
10.5 KRYPTOSYSTEME
![]()
EINFÜHRUNG |
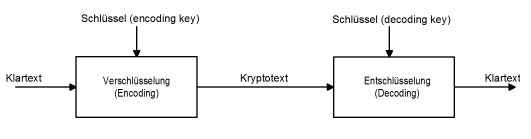
Das Geheimhalteprinzip spielt in unserer modernen Welt eine immer wichtigere Rolle. Zum Schutz der Privatsphäre, aber auch zur Geheimhaltung wichtiger staatlicher, industrieller und militärischer Informationen ist es nötig, Daten derart zu verschlüsseln, dass die verschlüsselten Daten wohl in die Hände von Unbefugten fallen können, es aber ohne Bekanntgabe der Entschlüsselungsmethode unmöglich oder zumindest sehr schwierig ist, die Originalinformation herauszufinden. Bei der Verschlüsselung (encoding) werden die Originaldaten in verschlüsselte (chiffrierte) Daten umgewandelt. Bei der Entschlüsselung (decoding) werden die Originaldaten wieder hergestellt. Verwendet man für die Daten das Buchstabenalphabet, so spricht man auch von Klartext und Kryptotext. Die Beschreibung des Verfahrens zum Entschlüsseln wird Schlüssel genannt. Es kann sich auch nur um eine einzige Zahl, eine Zahlen- oder eine Buchstabenfolge (ein Schlüsselwort) handeln. Wird beim Verschlüsseln und Entschlüsseln derselbe Schlüssel verwendet, so spricht man von einem symmetrischen Kryptoverfahren, andernfalls von einem asymmetrischen Kryptoverfahren.
|
CAESAR-VERSCHLÜSSELUNG |
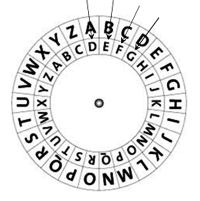
Nach der Überlieferung soll bereits Julius Cäsar (100 v.Chr. - 44 v.Chr.) folgendes Verfahren für seine militärische Korrespondenz angewendet haben: Jeder Buchstabe des Klartexts wird dabei alphabetisch um eine bestimmte feste Schlüsselzahl nach rechts verschoben, wobei man nach Z wieder bei A weiterfährt.
Der Encoder verschlüsselt den von der Datei eingelesene Textstring msg mit der Funktion encode(msg), wobei ausser für den Zeilenumbruch \n jedes Zeichen durch das entsprechende Kryptozeichen ersetzt wird. import string key = 4 alphabet = string.ascii_uppercase + " " def encode(text): enc = "" for ch in text: if ch != "\n": i = alphabet.index(ch) ch = alphabet[(i + key) % 27] enc += ch return enc fInp = open("original.txt") text = fInp.read() fInp.close() print("Original:\n", text) krypto = encode(text) print("Krypto:\n", krypto) fOut = open("secret.txt", "w") for ch in krypto: fOut.write(ch) fOut.close() Dein verschlüsselter Text sieht wie folgt aus:
Der Decoder ist ganz analog aufgebaut, nur dass die Zeichen im Alphabet rückwärts verschoben werden. import string key = 4 alphabet = string.ascii_uppercase + " " def decode(text): dec = "" for ch in text: if ch != "\n": i = alphabet.index(ch) ch = alphabet[(i - key) % 27] dec += ch return dec fInp = open("secret.txt") krypto = fInp.read() fInp.close() print("Krypto:\n", krypto) msg = decode(krypto) print("Message:\n", msg) fOut = open("message.txt", "w") for ch in msg: fOut.write(ch) fOut.close()
|
MEMO |
|
Beachte, dass du im Kryptotext auch alle Leerzeichen beibehalten musst, auch wenn diese am Anfang oder am Ende einer Zeile stehen. Es ist klar, dass die Verschlüsselung leicht geknackt werden kann. Es genügt beispielsweise, die Schlüsselzahlen 1..26 auszuprobieren |
VERSCHLÜSSELUNG NACH DEM VIGENÈRE-VERFAHREN |
import string key = "ALICE" alphabet = string.ascii_uppercase + " " def encode(text): keyList = [] for ch in key: i = alphabet.index(ch) keyList.append(i) print("keyList:", keyList) enc = "" for n in range(len(text)): ch = text[n] if ch != "\n": i = alphabet.index(ch) k = n % len(key) ch = alphabet[(i + keyList[k]) % 27] enc += ch return enc fInp = open("original.txt") text = fInp.read() fInp.close() print("Original:\n", text) krypto = encode(text) print("Krypto:\n", krypto) fOut = open("secret.txt", "w") for ch in krypto: fOut.write(ch) fOut.close()
Der Decoder ist wiederum praktisch identisch. import string key = "ALICE" alphabet = string.ascii_uppercase + " " def decode(text): keyList = [] for ch in key: i = alphabet.index(ch) keyList.append(i) print("keyList:", keyList) enc = "" for n in range(len(text)): ch = text[n] if ch != "\n": i = alphabet.index(ch) k = n % len(key) ch = alphabet[(i - keyList[k]) % 27] enc += ch return enc fInp = open("secret.txt") krypto = fInp.read() fInp.close() print("Krypto:\n", krypto) msg = decode(krypto) print("Message:\n", msg) fOut = open("message.txt", "w") for ch in msg: fOut.write(ch) fOut.close()
|
MEMO |
|
Die Vigenère-Verschlüsselung wurde bereits im 16. Jh. von Blaise de Vigenère erfunden und galt Jahrhunderte lang als sehr sicher. Kennt man die Länge 5 des Schlüsselworts, so muss man immerhin noch 265 = 11'881'376 Schlüsselzahlen durchprobieren, ausser man weiss etwas über das verwendete Wort, beispielsweise, dass es sich um den Vornamen einer Frau handelt. |
VERSCHLÜSSELUNG NACH DEM RSA-VERFAHREN |
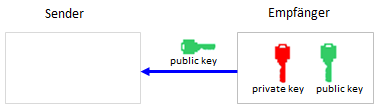
Bei diesem Verfahren, das nach ihren Erfindern Rivest, Shamir und Adleman benannt ist, wird ein Schlüsselpaar verwendet, nämlich ein privater (private key) und ein öffentlicher Schlüssel (public key). Die Originaldaten werden mit dem öffentlichen Schlüssel verschlüsselt und mit dem privaten Schlüssel entschlüsselt. Es handelt sich also um ein asymmetrisches Kryptoverfahren.
Die Schlüssel werden mit folgendem Algorithmus erzeugt, der auf der Zahlentheorie beruht [mehr... Einen elementaren Beweis findest du im Buch Barth, Algorithmik für Einsteiger, Springer-Verlag]. Zuerst werden zwei Primzahlen p und q gewählt, die für ein sicheres System mehrere hundert Stellen haben sollten. Man multipliziert diese und bildet m = p*q. Aus der Zahlentheorie weiss man, dass die Eulersche Funktion φ(m) = (p-1)*(q-1) die Zahl der teilerfremden Zahlen zu m ist (a, b sind teilerfremd, wenn der grösste gemeinsame Teiler ggT(a,b) = 1 ist). Als nächstes wählt man eine Zahl e, die kleiner als φ und teilerfremd zu φ ist. Damit ist der öffentliche Schlüssel bereits erstellt, er besteht aus dem Zahlenpaar:
Hier ein Beispiel mit den kleinen Primzahlen p = 73 und q = 151: m = 73 * 151 = 11023, φ = 72 * 150 = 10800, e = 11 (gewählt teilerfremd zu φ)
Der private Schlüssel besteht dann aus dem Zahlenpaar:
wobei für die Zahl d muss gelten: (d * e) mod φ = 1 (da e und φ teilerfremd sind, sagt das Lemma von Bézout aus der Zahlentheorie, dass die Gleichung mindestens eine Lösung hat). Du kannst mit deinen Werten für e und φ die Zahl d mit einem einfachen Programm bestimmen, indem du in einer for-Schleife 100 000 Werte für d ausprobierst. e = 11 phi = 10800 for d in range(100000): if (d * e) % phi == 1: print "d", d Du erhältst mehrere Lösungen (5891, 16691, 27491, 49091, usw.). Im Prinzip brauchst du aber nur die erste, um den privaten Schlüssel festzulegen.
Die Berechnung des privaten Schlüssels ist hier nur deswegen so einfach, da du die Zahlen p und q und damit auch die Zahl φ kennst. Ohne Kenntnis dieser Zahlen lässt sich der private Schlüssel nur mit einem grossen Aufwand berechnen Mit dem RSA-Algorithmus werden Zahlen verschlüsselt. Um einen Text zu verschlüsseln, verwendest du den ASCII-Code jedes Zeichens und bildest mit dem öffentlichen Schlüssel [m, e] den Verschlüsselungswert s für den Geheimtext gemäss der Formel
Diese Verschlüsselungszahlen schreibst du zeilenweise in die Datei secret.txt. publicKey = [11023, 11] def encode(text): m = publicKey[0] e = publicKey[1] enc = "" for ch in text: r = ord(ch) s = int(r**e % m) enc += str(s) + "\n" return enc fInp = open("original.txt") text = fInp.read() fInp.close() print("Original:\n", text) krypto = encode(text) print("Krypto:\n", krypto) fOut = open("secret.txt", "w") for ch in krypto: fOut.write(ch) fOut.close()
Im Decoder liest du die Zahlen von der Datei secret.txt zuerst in eine Liste. Zum Entschlüsseln berechnest du mit dem privaten Schlüssel aus der Verschlüsselungszahl s die ursprüngliche Zahl gemäss der Formel
Dies ist der ASCII-Code des ursprünglichen Zeichens. privateKey = [11023, 5891] def decode(li): m = privateKey[0] d = privateKey[1] enc = "" for c in li: s = int(c) r = s**d % m enc += chr(r) return enc fInp = open("secret.txt") krypto = [] while True: line = fInp.readline().rstrip("\n") if line == "": break krypto.append(line) fInp.close() print("Krypto:\n", krypto) msg = decode(krypto) print("Message:\n", msg) fOut = open("message.txt", "w") for ch in msg: fOut.write(ch) fOut.close()
|
||||||||||
MEMO |
|
Der grosse Vorteil des RSA-Verfahrens besteht darin, dass keine geheime Schlüsselinformation zwischen dem Sender und dem Empfänger ausgetauscht werden muss. Vielmehr generiert der Empfänger sowohl den öffentlichen und den privaten Schlüssel und teilt nur den öffentlichen Schlüssel dem Sender mit, behält aber den privaten Schlüssel bei sich geheim. Der Sender kann nun seine Daten verschlüsseln, aber nur der Empfänger kann sie entschlüsseln [mehr... Der Sender und Empfänger können auch über einen unsicheren Kanal, z. B. das Internet, verbunden sein]. In der Praxis wählt man die Primzahlen p und q sehr gross (mehrere Hundert Stellen lang). Die Generierung des öffentlichen Schlüssels erfordert nur die Produktbildung m = p * q, was sehr einfach ist. Will ein Hacker aus dem öffentlichen Schlüssel den privaten Schlüssel herausfinden, so muss er umgekehrt aus m die beiden geheimen Primfaktoren bestimmen. Das Faktorisieren einer langen Zahl ist aber bisher nur mit einem enormen Rechenaufwand möglich. Kryptosysteme nutzen also die Grenzen der Berechenbarkeit. Grundsätzlich gibt es aber kein absolut sichereres Verschlüsselungsverfahren. Die Verschlüsselung gilt aber bereits dann als sicher, wenn die Zeit für die Entschlüsselung wesentlich länger dauert als die Zeit, während der die Information von Wichtigkeit ist. |
AUFGABEN |
|