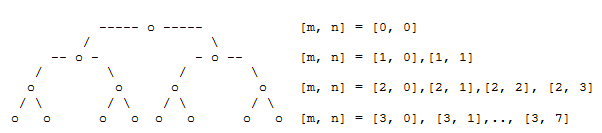Forum
10.3 BACKTRACKING
![]()
EINFÜHRUNG |
Bei der Entwicklung von Computergames wird es erst richtig interessant, wenn der Computer selbst zum intelligent handelnden Spielpartner wird. Dazu muss das Programm nicht nur die Spielregeln einhalten, sondern auch eine Gewinnstrategie verfolgen. Um eine Spielstrategie zu implementieren, wird das Spiel als Abfolge von Spielsituationen aufgefasst, die sich mit einer geeigneten Variablen s eindeutig identifizieren lassen. Man spricht auch von Spielzuständen und nennt darum s eine Zustandsvariable. Das Ziel einer Strategie ist es, von einem Anfangszustand zu einem Gewinnzustand zu gelangen, wobei das Spiel damit meist beendet ist. Die Spielzustände lassen sich anschaulich als Knoten in einem Spielgrafen aufzeichnen. Bei jedem Zug gibt es einen Übergang von einem Knoten zu einem seiner Nachfolgeknoten. Die Spielregeln legen fest, welches ausgehend von einem bestimmten Spielzustand die möglichen Nachfolgeknoten oder Nachbarn (neighbours) diese Spielzustands sind. Den Übergang zeichnet man als eine gerichtete Verbindungslinie, auch Kante genannt, ein [mehr... Die Spieltheorie baut ganz wesentlich auf der Grafentheorie, einem wichtigen Spezialgebiet der Mathematik auf.]. Hier lernst du wichtige Verfahren kennen, die allgemeine Gültigkeit haben und dir helfen, Computergames zu schreiben, die sogar gegen sehr intelligente menschliche Spieler gewinnen können. Allerdings gibt es für die meisten Spiele neben diesem allgemeinen Verfahren noch viel Platz für deine eigenen Ideen, effizientere, einfachere und dem speziellen Spiel besser angepasste Spielstrategien zu schreiben, die unter Umständen auch bessere Gewinnchancen haben. Auch viele politische, wirtschaftliche und soziale Systeme lassen sich als Spiel auffassen, sodass du deine hier erworbenen Kenntnisse auf eine weites praxisrelevantes Feld anwenden kannst. |
LÖSUNGSSUCHE FÜR EIN SOLOSPIEL |
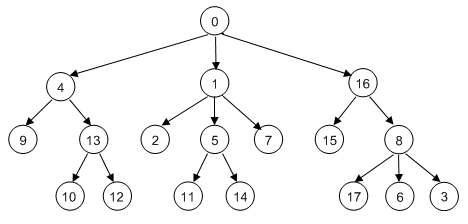
Wie erwähnt fasst du die Spielzustände als Knoten (nodes) in einem Graphen auf, der von Zug zu Zug durchlaufen wird. Dazu musst du die Spielzustände durch bestimmte Kriterien, z.B. die Anordnung der Spielfiguren auf einem Spielbrett, eindeutig identifizieren. Die Spielregeln legen fest, welches die möglichen Nachfolgeknoten oder Nachbarn (neighbours) eines bestimmten Spielzustands sind. Diese werden mit dem Knoten durch Linien (Kanten) verbunden. Da es sich um Nachfolgeknoten handelt, haben die Kanten eine Richtung vom Knoten zu seinem Nachbarn. Manchmal heisst ein Knoten auch "Mutter" und sein Nachbarn "Töchter", wobei die Möglichkeit offen gelassen wird, ob es auch eine Kante von einer Tochter zurück zur Mutter gibt. Du gehst hier zuerst von einem einfachen Spielgraphen für ein Spiel aus, das eine Person oder der Computer allein spielt. Das Einpersonenspiel oder Solospiel soll so aufgebaut sein, dass es keine Wege gibt, die wieder zurück führen. Damit ist sicher gestellt, dass du beim Durchlauf des Graphen nicht in einen Zyklus gerätst, der endlos durchlaufen wird. Ein solcher spezieller Graph heisst ein Baum. [mehr... Baum ist ein Graph ohne Zyklen] Die Knoten identifizierst du in irgend einer Reihenfolge mit Nummern zwischen 0 und 17. Der Graph hat folgende Struktur:
Der Baum soll als Ganzes in einer geeigneten Datenstruktur gespeichert werden. Dazu eignet sich eine Liste, in der die Nummern der Nachbarknoten als Teillisten enthalten sind, also beim Index 0 die Liste der Nachbarn von Knoten 0, beim Index 1 die Liste der Nachbarn von Knoten 1, usw. Enthält ein Knoten keine Nachbarn, so ist seine Nachbarliste leer [mehr... Einen solchen Knoten nennt man ein Blatt des Baums.]. Wie du leicht siehst, wird aus dem vorgegebenen Baum die Liste Die Identifikation der Knoten durch eine Nummer ist ein Trick und ermöglicht dir, die Nachbarn eines Knoten mit einem Listenindex zu bestimmen. Der Algorithmus zum Auffinden des Weges von einem bestimmten Knoten zu einem in der Baumstruktur tiefer liegenden Knoten wird in der Funktion search(node) rekursiv durchgeführt. In Pseudocode formuliert lautet er: suche(Knoten): Zusätzlich werden die "besuchten" Knoten hinten in der Liste visited eingetragen. Falls nicht vorher das Ziel erreicht wurde, wird nach dem Durchlauf aller Nachbarn der Knoten wieder aus visited entfernt, damit wieder der ursprüngliche Zustand hergestellt ist [mehr... visited hat also die Struktur eines Stacks (Last-In-First-Out) ]. Start- und Zielknotennummer können zu Programmbeginn eingegeben werden. neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13], [11, 14], [], [],
[17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []]
def search(node):
visited.append(node) # put (push) to stack
# Check for solution
if node == targetNode:
print "Target ", targetNode, "achieved. Path:", visited
targetFound = True
return
for neighbour in neighbours[node]:
search(neighbour) # recursive call
visited.pop() # redraw (pop) from stack
startNode = -1
while startNode < 0 or startNode > 17:
startNode = inputInt("Start node (0..17):")
targetNode = -1
while targetNode < 0 or targetNode > 17:
targetNode = inputInt("Target node (0..17):")
visited = []
search(startNode)
|
MEMO |
|
Für den Startknoten 0 und den Zielknoten 14 wird der richtige Weg [0, 1, 5, 14] ausgeschrieben. Fügst du beim Knoten 13 als Nachbar zusätzlich den Knoten 0 ein, so ergibt sich ein Zyklus und dies führt zu einer verhängnisvollen Situation, wo das Programm mit einem Laufzeitfehler abgebrochen wird, der sagt, dass die maximale Rekursionstiefe erreicht wurde. |
DURCHLAUF EINES ALIENS |
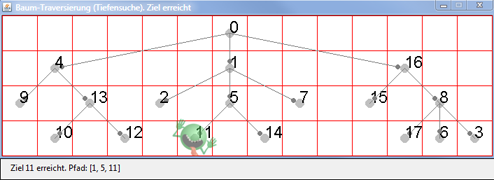
Es ist hübsch, den Algorithmus anschaulich zu verfolgen, indem du den Spielbaum grafisch aufzeichnest und schrittweise (mit einem Tastendruck) durchläufst. Dazu verwendest du am einfachsten ein GameGrid-Fenster, in welchem die Knoten bei gewissen Zellenkoordinaten (Locations) als Kreise sichtbar gemacht werden. In der aktuellen Zelle siehst du einen halbtransparenten Alien, der dir zuwinkt.
Den Baum zeichnest du mit den Grafikmethoden von GGBackground. Auf den Kanten kannst du mit getMarkerPoint() statt einem Pfeil eine kleine Kreismarkierung anbringen, um die Richtung der Kante zu zeigen. Achte darauf, dass du den Bildschirm mit refresh() aktualisieren musst. In der Statusbar kannst du wichtige Informationen anzeigen. from gamegrid import * neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13], [11, 14], [], [], [17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []] locations = [Location(6, 0), Location(6, 1), Location(4, 2), Location(13, 3), Location(1, 1), Location(6, 2), Location(12, 3), Location(8, 2), Location(12, 2), Location(0, 2), Location(1, 3), Location(5, 3), Location(3, 3), Location(2, 2), Location(7, 3), Location(10, 2), Location(11, 1), Location(11, 3)] def drawGraph(): getBg().clear() for i in range(len(locations)): getBg().setPaintColor(Color.lightGray) getBg().fillCircle(toPoint(locations[i]), 6) getBg().setPaintColor(Color.black) getBg().drawText(str(i), toPoint(locations[i])) for k in neighbours[i]: drawConnection(i, k) refresh() def drawConnection(i, k): getBg().setPaintColor(Color.gray) startPoint = toPoint(locations[i]) endPoint = toPoint(locations[k]) getBg().drawLine(startPoint, endPoint) getBg().fillCircle(getMarkerPoint(endPoint, startPoint, 10), 3) def search(node): global targetFound if targetFound: return visited.append(node) # put (push) to stack alien.setLocation(locations[node]) refresh() if node == targetNode: setStatusText("Target " + str(targetNode) + "achieved. Path: " + str(visited)) targetFound = True return else: setStatusText("Current node " + str(node) + " . Visited: " + str(visited)) getKeyCodeWait(True) # exit if GameGrid is disposed for neighbour in neighbours[node]: search(neighbour) # Recursive call visited.pop() makeGameGrid(14, 4, 50, Color.red, False) setTitle("Tree-traversal (depth-first search). Press a key...") addStatusBar(30) show() setBgColor(Color.white) drawGraph() startNode = -1 while startNode < 0 or startNode > 17: startNode = inputInt("Start node (0..17):") targetNode = -1 while targetNode < 0 or targetNode > 17: targetNode = inputInt("Target node (0..17):") visited = [] targetFound = False alien = Actor("sprites/alieng_trans.png") addActor(alien, locations[startNode]) search(startNode) setTitle("Tree-traversal (depth-first search). Target achieved")
|
MEMO |
|
Wie du siehst, bewegt sich der Alien zu den Töchterknoten "in die Tiefe des Baums" und springt dann auf den letzten Mutterknoten zurück. Aus diesem Grund nennt man das Verfahren Tiefensuche mit Backtracking (depth-first search). |
DER ALIEN AUF DEM WEG ZURÜCK |
Willst du sichtbar machen, auf welchem Weg sich der Alien beim Rückzug bewegt, so musst du die Knotenfolge bei der Vorwärtsbewegung in einer Liste steps abspeichern. In jeder Rekursionstiefe gibt es wieder eine neue Liste und du speicherst diese in stepsList. Nach der Rückkehr musst du den letzten Eintrag mit stepList.pop() entfernen. from gamegrid import * neighbours = [[4, 1, 16], [2, 5, 7], [], [], [9, 13], [11, 14], [], [], [17, 6, 3], [], [], [], [], [10, 12], [], [], [15, 8], []] locations = [Location(6, 0), Location(6, 1), Location(4, 2), Location(13, 3), Location(1, 1), Location(6, 2), Location(12, 3), Location(8, 2), Location(12, 2), Location(0, 2), Location(1, 3), Location(5, 3), Location(3, 3), Location(2, 2), Location(7, 3), Location(10, 2), Location(11, 1), Location(11, 3)] def drawGraph(): getBg().clear() for i in range(len(locations)): getBg().setPaintColor(Color.lightGray) getBg().fillCircle(toPoint(locations[i]), 6) getBg().setPaintColor(Color.black) getBg().drawText(str(i), toPoint(locations[i])) for k in neighbours[i]: drawConnection(i, k) refresh() def drawConnection(i, k): getBg().setPaintColor(Color.gray) startPoint = toPoint(locations[i]) endPoint = toPoint(locations[k]) getBg().drawLine(startPoint, endPoint) getBg().fillCircle(getMarkerPoint(endPoint, startPoint, 10), 3) def search(node): global targetFound if targetFound: return visited.append(node) # put (push) to stack alien.setLocation(locations[node]) refresh() if node == targetNode: setStatusText("Target " + str(targetNode) + "achieved. Path: " + str(visited)) targetFound = True return else: setStatusText("Current nodes " + str(node) + " . Visited: " + str(visited)) getKeyCodeWait(True) # exit if GameGrid is disposed for neighbour in neighbours[node]: steps = [node] stepsList.append(steps) steps.append(neighbour) search(neighbour) # Recursive call steps.reverse() if not targetFound: for loc in steps[1:]: setStatusText("Go back") alien.setLocation(locations[loc]) refresh() getKeyCodeWait() stepsList.pop() visited.pop() makeGameGrid(14, 4, 50, Color.red, False) setTitle("Tree-traversal (depth-first search). Press a key...") addStatusBar(30) show() setBgColor(Color.white) drawGraph() startNode = -1 while startNode < 0 or startNode > 17: startNode = inputInt("Start node (0..17):") targetNode = -1 while targetNode < 0 or targetNode > 17: targetNode = inputInt("Target node (0..17):") visited = [] stepsList = [] targetFound = False alien = Actor("sprites/alieng_trans.png") addActor(alien, locations[startNode]) search(startNode) setTitle("Tree-traversal (depth-first search). Target achieved")
|
MEMO |
|
Der Alien bewegt sich nun tatsächlich im Baum wieder nach oben, wodurch es besonders deutlich wird, warum der Algorithmus Backtracking heisst. Das rekursive Backtracking spielt bei vielen Algorithmen eine wichtige Rolle und wird manchmal auch als "Schweizer Taschenmesser der Informatiker" bezeichnet. |
STRATEGIE IM IRRGARTEN |
Manchmal ist es schwierig, ja geradezu beängstigend, den Ausgang aus einem Irrgarten zu finden. Du kannst aber nun mit deinem Wissen über Backtracking ein Programm schreiben, dass den Ausgang mit Sicherheit findet. Es ist offensichtlich, dass du einen Irrgarten, der keine Zyklen aufweist, als Baum modellieren kannst und darum das Auffinden des Ausgang einer Baumsuche entspricht. Du verwendest hier nur ein kleines Zufallslabyrinth mit 11x11 Zellen. Per Tastendruck führt der Alien einen Schritt aus, drückst du aber die Enter-Taste, so sucht er den Ausgang völlig autonom. Das Labyrinth erzeugst du mit der Klasse Maze. Dabei übergibst du die gewünschte Anzahl der Zeilen und Spalten als ungerade Zahlen. Es entsteht jedesmal ein anderes zufälliges Labyrinth mit einem Eingang oben an der linken und einem Ausgang unten an der rechten Seite. Mit isWall(loc) kannst du testen, ob sich an der Location loc eine Wandzelle befindet.
from gamegrid import * def createMaze(): global maze maze = GGMaze(11, 11) for x in range(11): for y in range(11): loc = Location(x, y) if maze.isWall(loc): getBg().fillCell(loc, Color(0, 50, 0)) else: getBg().fillCell(loc, Color(255, 228, 196)) refresh() def getNeighbours(node): neighbours = [] for loc in node.getNeighbourLocations(0.5): if isInGrid(loc) and not maze.isWall(loc): neighbours.append(loc) return neighbours def search(node): global targetFound, manual if targetFound: return visited.append(node) # push alien.setLocation(node) refresh() delay(500) if manual: if getKeyCodeWait(True) == 10: #Enter setTitle("Finding target...") manual = False # Check for termination if node == exitLocation: targetFound = True for neighbour in getNeighbours(node): if neighbour not in visited: backSteps = [node] backStepsList.append(backSteps) backSteps.append(neighbour) search(neighbour) # recursive call backSteps.reverse() if not targetFound: for loc in backSteps[1:]: setTitle("Must go back...") alien.setLocation(loc) refresh() delay(500) if manual: setTitle("Went back. Press key...") else: setTitle("Went back. Find target...") backStepsList.pop() visited.pop() # pop manual = True targetFound = False visited = [] backStepsList = [] makeGameGrid(11, 11, 40, False) setTitle("Press a key. (<Enter> for automatic") show() createMaze() startLocation = maze.getStartLocation() exitLocation = maze.getExitLocation() alien = Actor("sprites/alieng.png") addActor(alien, startLocation) search(startLocation) setTitle("Target found")
|
MEMO |
|
Es ist interessant, die Lösungsstrategie des Menschen mit der des Computers zu vergleichen. Ein menschlicher Spieler erkennt auf einem Blick die Gesamtsituation und leitet daraus eine Strategie ab, wie er möglichst schnell zum Ausgang gelangt. Er handelt dabei mit einer für Menschen typischen globalen Übersicht, die deinem Computerprogramm fehlt. Dieses erfasst die momentane Situation nur lokal, "erinnert" sich aber dafür sehr genau an die bereits durchlaufenen Wege und durchsucht sehr systematisch neue Wege zum Ziel. Die Situation ändert sich aber zu Gunsten des Computers, wenn man dem menschlichen Menschen die globale Übersicht vorenthält, z.B. wenn er sich selbst im Innern des Labyrinths befindet und man nicht über die Wände sieht. |
AUFGABEN |
|
ZUSATZSTOFF |
DAS N-DAMEN PROBLEM |
Es handelt sich um ein schachtechnisches Problem, das bereits Mitte des 19. Jahrhunderts diskutiert wurde. Es gilt dabei, auf einem Schachbrett mit nxn-Feldern n Damen so zu platzieren, dass sie sich gemäss den Schachregeln gegenseitig nicht schlagen können. (Die Schachregeln besagen, dass sich eine Dame horizontal und vertikal, sowie auf der Diagonalen bewegen kann.) Es gibt zwei Fragestellungen mit ganz unterschiedlichem Schwierigkeitsgrad: Zum einen möchte man eine Lösung angeben, zum anderen möchte man herausfinden, wieviele Lösungen es insgesamt gibt. Bereits 1874 bewies der Mathematiker Glaisher, dass es für das klassische Schachbrett mit n = 8 insgesamt 92 Lösungen gibt. Das Damenproblem gilt als Musterbeispiel für das Backtracking. Dabei setzt man Zug um Zug eine Dame nach der anderen derart auf das Brett, dass die neue Dame nicht in Konflikt mit den bereits vorhandenen gerät. Geht man ziellos vor, so gibt es meist vor Ende der Aufstellung einen Moment, wo dies nicht mehr möglich ist. Die beim Backtracking angewendete Strategie besteht darin, dass man den letzten Zug zurücknimmt und es mit einer Alternative versucht. Gibt es auch jetzt keine Lösung, so muss man auch diesen Zug zurücknehmen, usw. Der Mensch verliert bei diesem Vorgehen leicht die Übersicht, welche Stellungen bereits geprüft wurden, der Computer hat dagegen damit kein Problem, weil er rein systematisch vorgeht.
Im Backtracking-Algorithmus bestimmst du die Nachbarknoten des aktuellen Knotens node mit der Funktion getNeighbours(node). Dabei gehst du von der eindimensionalen Datenstruktur auf Locations über, welche die x und y Koordinate der Felder verwendet. In der die Liste squares sammelst du die bereits besetzten Felder und in der Liste forbidden diejenigen, die auf Grund der Spielregeln nicht besetzt werden dürfen. (Dabei ist es praktisch, die Methode getDiagonalLocations() zu verwenden.) Schliesslich bildest du die Liste allowed der noch besetzbaren Felder. In den Nachbarknoten musst du nun die -1 durch den Spaltenindex ersetzen, auf den die neue Dame gesetzt wird In search() implementierst du den dir bereits bekannten Backtracking-Algorithmus. Sobald eine Lösung gefunden wurde, brichst du die weitere Suche ab (Rekursionsstopp). from gamegrid import * n = 8 # number of queens def getNeighbours(node): squares = [] # list of occupied squares for i in range(n): if node[i] != -1: squares.append(Location(node[i], i)) forbidden = [] # list of forbidden squares for location in squares: a = location.x b = location.y for x in range(n): forbidden.append(Location(x, b)) # same row for y in range(n): forbidden.append(Location(a, y)) # same column for loc in getDiagonalLocations(location, True): #diagonal up forbidden.append(loc) for loc in getDiagonalLocations(location, False): #diagonal down forbidden.append(loc) allowed = [] # list of all allowed squares = all - forbidden for i in range(n): for k in range(n): loc = Location(i, k) if not loc in forbidden: allowed.append(loc) neighbourNodes = [] for loc in allowed: neighbourNode = node[:] i = loc.y # row k = loc.x # col neighbourNode[i] = k neighbourNodes.append(neighbourNode) return neighbourNodes def search(node): global found if found or isDisposed(): return visited.append(node) # node marked as visited # Check for solution if not -1 in node: found = True drawNode(node) for s in getNeighbours(node): search(s) visited.pop() def drawBoard(): for i in range(n): for k in range(n): if (i + k) % 2 == 0: getBg().fillCell(Location(i, k), Color.white) def drawNode(node): removeAllActors() for i in range(n): addActorNoRefresh(Actor("sprites/chesswhite_1.png"),Location(node[i],i)) refresh() makeGameGrid(n, n, 600 // n, False) setBgColor(Color.darkGray) drawBoard() show() setTitle("Searching. Please wait..." ) visited = [] found = False startNode = [-1] * n # all squares empty search(startNode) setTitle("Search complete. ")
|
MEMO |
|
Je nach Leistung deines Rechners musst du einige Sekunden bis einige Minuten warten, bis eine Lösung gefunden wird. Dauert es dir zulange, so kannst du n = 6 setzen. |
AUFGABEN |
|