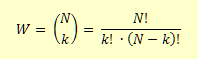EINFÜHRUNG

Obschon das Wort Information oft verwendet wird, ist es gar nicht so leicht, den Begriff exakt zu fassen und messbar zu machen. Im täglichen Leben wird mehr Information mit mehr Wissen verbunden und gesagt, dass eine informierte Person A in einer gewissen Sache mehr weiss als eine nicht informierte Person B.

Um die Mehrinformation von A gegenüber B (oder dem Team B) bzw. den Informationsmangel von B gegenüber A zu messen, stellst du dir am besten ein TV-Fragespiel vor. Dabei muss eine Person B oder ein Team etwas herausfinden, was nur die Person A weiss, beispielsweise ihren Beruf. Dabei stellt B Fragen, die A stets mit Ja oder Nein beantworten muss. Man definiert:

Unter dem Informationsmangel I von B gegenüber A (in bit) versteht man die Anzahl Fragen mit Ja/Nein-Antwort, die B (im Mittel und bei optimaler Fragestrategie) stellen muss, um über eine bestimmte Sache das gleiche Wissen wie A zu haben.

ZAHLEN-RATESPIEL

Ein solches Ratespiel kannst du (auch nur in Gedanken) in deiner Schulklasse wie folgt inszenieren: Eure Klassenkameradin Judith wird vor die Tür geschickt. Einer der verbleibenden W = 16 Kameraden, erhält ein "begehrliches" Objekt, beispielsweise einen  Schokoladenriegel. Nachdem Judith wieder in die Schulstube zurückgerufen wird, wissen du und deine Kameraden, wer der Schokoladenbesitzer ist, Judith aber nicht. Wie gross ist ihr Informationsmangel?

Der Einfachheit halber werden die Kameraden von 0 bis 15 numeriert und Judith kann euch nun Fragen stellen, um die geheime Zahl des Schokoladenbesitzers herauszufinden. Je weniger Fragen sie dazu braucht, je besser. Eine Möglichkeit wäre, irgendwelche zufälligen Zahlen abzufragen: "Ist es 13?" und wenn eine Nein-Antwort kommt, nach einer anderen Zahl zu fragen.

Judith könnte auch systematisch vorgehen und von 0 an fragen: "Ist es die 0?", dann "Ist es die 1?", usw. In deiner Computersimulation bestimmst du, wie viele Fragen sie mit dieser Frageart benötigt, um im Mittel (d.h. wenn man das Spiel oft spielt) die Geheimzahl herauszufinden. Dabei überlegst du Folgendes:

Wenn die Geheimzahl 0 ist, so braucht man 1 Frage, ist sie 1, so sind 2 Fragen nötig, usw. Wenn die Geheimzahl 14 ist, so sind 15 Fragen nötig, aber wenn sie 15 ist, so sind ebenfalls 15 Fragen nötig, da man bei der 15. Frage "Ist es 14?" Nein als Antwort erhält und weiss, dass es die 15 ist. Das Programm spielt das Spiel 100000 mal und zählt jeweils die Anzahl Fragen, bis die Geheimzahl ermittelt wurde. Die Zahl der Fragen wird aufsummiert, um zuletzt den Mittelwert zu bestimmen.

from random import randint

sum = 0
z = 100000
repeat z:
    n = randint(0, 15)
    if n != 15:
        q = n + 1 # number of questions
    else:
       q = 15
    sum += q   
print("Mean:", sum / z)

Mit dieser Fragestrategie würde Judith im Mittel 8.43 Fragen benötigen. Das ist sehr viel. Da aber Judith gescheit ist, wählt sie eine viel bessere Fragestrategie. Sie fragt euch: "Ist es eine Zahl zwischen 0 und 7?" (Grenzen eingeschlossen). Falls ihr Ja sagst, so teilt sie den Bereich wieder in zwei gleich grosse Teile und fragt: "Ist die Zahl zwischen 0 und 3? ", falls ihr Ja sagt, so fragt sie "Ist es 0 oder 1?". Falls ihr Ja sagt, so fragt sie "Ist es 0?" und sie kennt die Zahl. Mit dieser "binären" Fragestrategie muss Judith  bei W = 16 immer genau 4 Fragen stellen, also ist 4 auch die mittlere Anzahl Fragen. Die binäre Fragestrategie ist optimal und die Information über den Riegelbesitzers hat daher den Wert I = 4 bit.

MEMO

INFORMATIONSGEHALT EINES WORTS

Da die W Zustände gleichwahrscheinlich sind, ist die Wahrscheinlichkeit für einen der Zustände p = 1/W und du kannst die Information auch so schreiben:

                                               I = ld(1/p) = -ld(p)

Es ist dir sicher bekannt, dass die Wahrscheinlichkeit für einen bestimmten Buchstaben in einer gesprochenen Sprache ganz unterschiedlich ist. Die folgende Tabelle zeigt die Wahrscheinlichkeiten für die deutsche Sprache [mehr... Die Werte hängen von der Art des Textes ab. Die Zahlen entsprechen einem literarischen Text].

Es ist natürlich nicht so, dass die Wahrscheinlichkeit für einen Buchstaben in einem Wort unabhängig davon ist, welche Buchstaben des Worts man bereits kennt und in welchem Zusammenhang das Wort steht. Macht man aber diese vereinfachende Annahme, so gilt für die Wahrscheinlichkeit p einer Buchstabenkombination aus zwei Buchstaben mit den Einzelwahrscheinlichkeiten p₁ und p₂ gemäss der Produktregel p = p₁ * p₂ und für die Information

I = -ld(p) = -ld(p₁*p₂ ) = -ld(p₁ ) - ld(p₂ )

oder für beliebig viele Buchstaben:

I = - ld(p₁ ) - ld(p₂ ) - ld(p₃ ) - ... - ld(p_n ) = - Σ ld(p_i )

In deinem Programm kannst du ein Wort eingeben und du erhältst als Ausgabe den Informationsgehalt des Worts. Dabei solltest du die Dateien mit den Buchstabenhäufigkeiten in deutsch, englisch und französisch von hier downloaden und in das Verzeichnis kopieren, in dem dein Python-Programm ist.

from math import log

f = open("letterfreq_de.txt")
s = "{"
for line in f:
    line = line[:-1] # remove trailing \n
    s += line + ", "
f.close()
s = s[:-2]  # remove trailing ,
s += "}"
occurance = eval(s)

while True:
    word = inputString("Enter a word")
    I = 0
    for letter in word.upper():
        p = occurance[letter] / 100
        I -= log(p, 2)
    print(word, "-> I =", round(I, 2), "bit")   

MEMO

AUFGABEN

ZUSATZSTOFF

DER ZUSAMMENHANG ZWISCHEN UNORDNUNG UND ENTROPIE

Es gibt einen äusserst interessanten Zusammenhang zwischen der Information, die wir über ein System haben und der Ordnung des Systems. Sitzen beispielsweise in einem Klassenzimmer alle Schülerinnen und Schüler an ihren Pulten, so ist die Ordnung sicher viel grösser als wenn sie sich wahllos im Zimmer herumbewegen. Im ungeordneten Zustand ist unser Informationsmangel, wo sich jede einzelne Person befindet, sehr gross, darum kann man diesen Informationsmangel als Mass für die Unordnung heranziehen. Dazu definiert man den Begriff der Entropie:

Unter der Entropie (in bit) verstehen wir den Informationsmangel I, den wir bei einer makroskopischen Beschreibung des Systems gegenüber jemandem besitzen, der den mikroskopischen Zustand kennt. Für die Entropie in (J/K) setzen wir S = k * ln2 * I Der Faktor k heisst Bolzmann-Konstante. Bis auf einen Vorfaktor sind also Entropie und Informationsmangel dasselbe. Gehen wir von einem System mit W gleichwahrscheinlichen Zuständen aus, so haben wir S = k * ln2 * ldW oder      S = k * log W Diese fundamentale Beziehung stammt vom grossen Physiker Ludwig Boltzmann (1844-1900) und steht auf seiner Grabinschrift.

Wie du feststellen kannst, haben sich selbst überlassene Systeme die Tendenz, von einem geordneten in einen ungeordneten Zustand überzugehen. Beispielsweise:

• Passagiere in einem Eisenbahnwagen verteilen sich über den ganzen Wagen
• Zigarettenrauch verteilt sich im Zimmer
• Tintenklecks verteilt sich im Wasserglas
• Temperatur zwischen Kaffee und Tasse gleicht sich aus

Da der ungeordnete Zustand eine höhere Entropie als der geordnete hat, kann man dies als Naturgesetz (2. Hauptsatz der Thermodynamik) formulieren: In einem abgeschlossenen System nimmt die Entropie zu oder bleibt gleich, nimmt aber nie ab. Mit deinem Programm simulierst du ein Teilchensystem, bei dem die Teilchen wie Gasatome miteinander zusammenstossen und dabei ihre Richtung und ihre Bewegungsenergie austauschen. Zuerst befinden sich alle Teilchen im linken Teil eines Behälters, der eine Trennwand mit einem Loch aufweist. Was passiert?

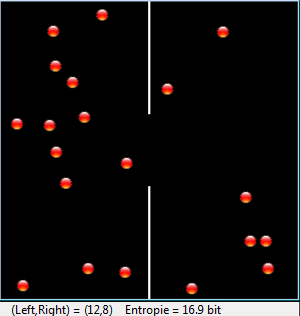
Für die Animation wird das Modul gamegrid herangezogen. Die Teilchen sind in der Klasse Particle modelliert, die aus der Klasse Actor abgeleitet ist. In der Methode act(), die in jedem Simulationszyklus automatisch aufgerufen wird, bewegst du die Teilchen. Die Kollisionen werden mit Kollisionsevents behandelt. Dazu leitest du die Klasse CollisionListener aus GGActorCollisionListener ab und überschreibst die Methode collide(). Das Vorgehen ist das Gleiche wie im Kapitel 8.10 Brownsche Bewegung. Die 20 Teilchen werden in 4 verschiedene Geschwindigkeitsgruppen eingeteilt. Da beim Zusammenstoss die Geschwindigkeiten ausgetauscht werden, bleibt die Gesamtenergie des Systems konstant, d.h. das System ist abgeschlossen.

from gamegrid import *
from gpanel import *
from math import log

# =================== class Particle ====================
class Particle(Actor):
    def __init__(self):
        Actor.__init__(self, "sprites/ball_0.gif")
 
    # Called when actor is added to gamegrid
    def reset(self):
        self.isLeft = True
  
    def advance(self, distance):
        pt = self.gameGrid.toPoint(self.getNextMoveLocation())
        dir = self.getDirection()
        # Left/right wall
        if pt.x < 0 or pt.x > w:
            self.setDirection(180 - dir)
        # Top/bottom wall
        if pt.y < 0 or pt.y > h:
            self.setDirection(360 - dir)
        # Separation
        if (pt.y < h // 2 - r or pt.y > h // 2 + r) and \
            pt.x > self.gameGrid.getPgWidth() // 2 - 2 and \
            pt.x < self.gameGrid.getPgWidth() // 2 + 2:
                self.setDirection(180 - dir)

        self.move(distance)
        if self.getX() < w // 2:
            self.isLeft = True
        else:
            self.isLeft = False

    def act(self):
        self.advance(3)
        
    def atLeft(self):
        return self.isLeft

# =================== class CollisionListener =========
class CollisionListener(GGActorCollisionListener):
    # Collision callback: just exchange direction and speed
    def collide(self, a,  b):
        dir1 = a.getDirection()
        dir2 = b.getDirection()
        sd1 = a.getSlowDown()
        sd2 = b.getSlowDown()
        a.setDirection(dir2)
        a.setSlowDown(sd2)
        b.setDirection(dir1)
        b.setSlowDown(sd1)
        return 5  # Wait a moment until collision is rearmed


# =================== Global sections =================
def drawSeparation():
    getBg().setLineWidth(3)
    getBg().drawLine(w // 2, 0, w // 2, h // 2 - r)
    getBg().drawLine(w // 2, h, w // 2, h // 2 + r)

def init():
    collisionListener = CollisionListener()
    for i in range(nbParticles):
        particles[i] = Particle()

        # Put them at random locations, but apart of each other
        ok = False
        while not ok:
            ok = True
            loc = getRandomLocation()
            if loc.x > w / 2 - 20:
                ok = False
            continue

        for k in range(i):
            dx = particles[k].getLocation().x - loc.x
            dy = particles[k].getLocation().y - loc.y
            if dx * dx + dy * dy < 300:
                ok = False
        addActor(particles[i], loc, getRandomDirection())
        delay(100)

        # Select collision area
        particles[i].setCollisionCircle(Point(0, 0), 8)
        # Select collision listener 
        particles[i].addActorCollisionListener(collisionListener)

        # Set speed in groups of 5
        if i < 5:
            particles[i].setSlowDown(2)
        elif i < 10:
            particles[i].setSlowDown(3)
        elif i < 15:
            particles[i].setSlowDown(4)
    
    # Define collision partners
    for i in range(nbParticles):
        for k in range(i + 1, nbParticles):
            particles[i].addCollisionActor(particles[k])

def binomial(n, k):
    if k < 0 or k > n:
        return 0
    if k == 0 or k == n:
        return 1
    k = min(k, n - k) # take advantage of symmetry
    c = 1
    for i in range(k):
        c = c * (n - i) / (i + 1)
    return c
                                    
r = 50  # Radius of hole
w = 400
h = 400
nbParticles = 20
particles = [0] * nbParticles
makeGPanel(Size(600, 300))
window(-6, 66, -2, 22)
title("Entropy")
windowPosition(600, 20)
drawGrid(0, 60, 0, 20)
makeGameGrid(w, h, 1, False)
setSimulationPeriod(10)
addStatusBar(20)
drawSeparation()
setTitle("Entropy")
show()
init()
doRun()

t = 0
while not isDisposed():
    nbLeft = 0
    for particle in particles:
        if particle.atLeft():
            nbLeft += 1
    entropy = round(log(binomial(nbParticles, nbLeft), 2), 1)
    setStatusText("(Left,Right) = (" + str(nbLeft) + "," + 
    str(nbParticles-nbLeft)+ ")"+" Entropie = "+str(entropy)+" bit")
    if t % 60 == 0:
        clear()
        lineWidth(1)
        drawGrid(0, 60, 0, 20)
        lineWidth(3)
        move(0, entropy)
    else:
        draw(t % 60, entropy)
    t += 1
    delay(1000)
dispose() # GPanel

MEMO

AUFGABEN