Fadengrafik

deutsch english français Drucken

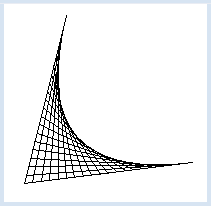
3.8 FADENGRAFIKEN

EINFÜHRUNG

Schon im Kindergarten hast du wahrscheinlich mit Fadengrafiken gespielt. Dabei musstest du gemäss einer Bastel-Anleitung entlang einer bestimmten Figur in ein Holz- oder Kartonbrett Nägel einschlagen oder Nadeln einstecken. Meist waren diese in gleichen Abständen angeordnet. Mit Fäden hast du sie dann miteinander verbunden. Wenn du genügend viele Fäden legst, erscheinen bei den Fadenverdichtungen interessante Kurven, die man in der Mathematik Enveloppe (auch Hüllkurve) nennt, da die Fäden Tangenten an diese Kurven sind.

Aus Täubner, Walz: Fadengrafik

Statt die Fadengrafik selbst zu erzeugen, könntest du auch eine Maschine damit beauftragen. Diese müsste die Anleitung verstehen und dann in eine Aktion umsetzen, beispielsweise mit einem Roboterarm die Fäden ziehen oder die Fäden auf einem Bildschirm aufzeichnen. Eine solche Anleitung für eine Maschine nennt man auch Algorithmus. Man kann den Algorithmus zwar wie eine Bastel-Anleitung zuerst allgemein verständlich in einer Umgangssprache formulieren. Da es aber erwünscht ist, dass die Maschine bei jedem Durchlauf genau dasselbe Muster erzeugt, muss der Algorithmus so exakt formuliert sein, dass die Maschine bei jedem Schritt eindeutig weiss, was zu tun ist. Dazu hat man die Programmiersprachen erfunden und darum lernst du programmieren, denn in der natürlichen Sprache gibt es keine solche Eindeutigkeit.

PROGRAMMIERKONZEPTE: Algorithmus, Datenstruktur, Modell, Programmeleganz, Liste, Index

PUNKTE ALS LISTEN

Statt mit Brett, Nägeln und Fäden zu arbeiten, kannst du den Vorgang auf den Computer übertragen. Dabei machst du dir ein Abbild der Natur, du modellierst das Brett als Bildschirmfenster, die Nägel als Bildschirmpunkte und die Fäden als Linien.

Bei der Übertragung des Algorithmus in eine Programmiersprache ist es wichtig, eine möglichst enge Beziehung zur Wirklichkeit herzustellen. Nägel bzw. geometrische Punkte stellen für dich handfeste Objekte dar und so sollte es im Programm auch sein.

In der Geometrie schreibst du für einen Punkt P(x, y), wo x und y die Koordinaten sind. Im Programm können wir die zwei Zahlen x und y in eine Datenstruktur verpacken, die wir eine Liste nennen. Wir schreiben p = [x, y]. Der geometrische Punkt P(0, 8) wird also durch die Liste p = [0, 8] modelliert.

Auf die einzelnen Komponenten einer Liste kannst du mit einem Index zugreifen, wobei die Zählung bei 0 beginnt. Du schreibst den Index in eine eckiges Klammerpaar, also für die x-Koordinate p[0] und für die y-Koordinate p[1].

Das Schöne daran ist, dass alle Grafikfunktionen von GPanel "listenbewusst" sind, denn sie funktionieren statt mit x-y-Koordinaten auch mit Punkt-Listen. Dein Programm modelliert das Ziehen der Fäden von einem Nagel A über 19 Nägel bei den Koordinaten auf der x-Achse zum Nagel B und wieder zurück. Du kannst sogar ein delay() einbauen, das bewirkt, dass das Fadenziehen tatsächlich eine für Menschen erfassbare Zeit lang dauert.

from gpanel import *

DELAY = 100

def step(x):
    p1 = [x, 0]
    draw(p1)
    delay(DELAY)
    draw(pB)
    delay(DELAY)
    p2 = [x + 1, 0]
    draw(p2) 
    delay(DELAY)
    draw(pA) 
    delay(DELAY)

makeGPanel(-10, 10, -10, 10)
pA = [0, 8]
pB = [0, -8]
move(pA)
for x in range(-9, 9, 2):
    step(x)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Bei der Implementierung eines Algorithmus müssen auch die Daten günstig strukturiert werden. Bei uns werden geometrische Punkte als Listen mit zwei Elementen (x- und y-Koordinaten) modelliert. Die Wahl der Datenstruktur beeinflusst das Programm ganz wesentlich. Niklaus Wirth, ein berühmter Informatikprofessor an der ETH Zürich, sagte treffend: Programm = Algorithmus + Datenstruktur [Lit.]
Listen können mehrere Werte, genannt Listenelemente speichern. Listen werden mit eckigen Klammern definiert. Man kann mit einem Listenindex die einzelnen Elemente lesen und ihnen neue Werte zuweisen.

Alle Grafikbefehle von GPanel funktionieren auch mit Punkten, die als Listen mit x- und y-Koordinaten modelliert sind.

PROGRAMMIEREN IST EINE KUNST

Du merkst sicher, dass du die eben erstellte Fadengrafik viel einfacher erzeugen kannst, wenn du die Linien unabhängig davon zeichnest, wie der Faden tatsächlich von Hand gezogen würde. Du brauchst ja nur die Punkte A und B mit Strecken zu verbinden.

from gpanel import *

makeGPanel(-10, 10, -10, 10)
pA = [0, 8]
pB = [0, -8]

for x in range(-9, 10, 1):
    pX = [x, 0]
    line(pA, pX)
    line(pB, pX)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Ein Algorithmus kann auf verschiedene Arten implementiert werden, die sich in der Länge des Codes und in der Laufzeit des Programms unterscheiden. Man spricht auch von eleganten und weniger eleganten Programmen. Merke dir, dass es nicht genügt, dass ein Programm ein richtiges Resultat hervorbringt, sondern dass es auch elegant geschrieben ist. Fasse darum Programmieren als eine Kunst auf.

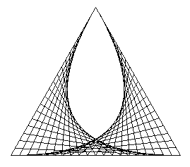
ELEGANTE FADENGRAFIK-ALGORITHMEN

Für Fadengrafiken benötigst du oft Teilungspunkte (dividing points) einer Strecke. Dazu gibt es in GPanel eine einfache Funktion getDividingPoint(pA, pB, r), der du die zwei Endpunkte pA und pB der Strecke und den Teilungsfaktor r übergibst. Sie liefert dir den Teilungspunkt als Liste zurück.

Du modellierst nun eine Fadengrafik mit Nägeln auf den Seiten AB und AC mit einem besonders eleganten Programm.

from gpanel import *

makeGPanel(0, 100, 0, 100)
     
pA = [10, 10]
pB = [90, 20]
pC = [30, 90]

line(pA, pB)
line(pA, pC)

r = 0
while r <= 1:
    pX1 = getDividingPoint(pA, pB, r)
    pX2 = getDividingPoint(pA, pC, 1 - r)
    line(pX1, pX2)
    r += 0.05
    delay(300)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Bibliotheksfunktionen, wie hier getDividingPoint(), können ein Programm stark vereinfachen. Für bestimmte wohldefinierte Teilaufgaben solltest du vorhandene Bibliotheksfunktionen verwenden, die du von deiner Programmiererfahrung her kennst, aus Dokumentationen entnimmst oder mit Web-Suchmaschinen findest.

Mathematisch betrachtet ist die entstehende Kurve eine quadratische Bézierkurve. Du kannst sie mit der Funktion quadraticBezier(pB, pA, pC) zeichnen (pB und pC sind die Endpunkte, pA der Kontrollpunkt der Kurve).

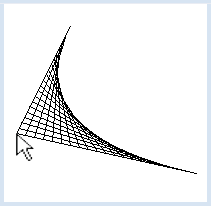
MAUSGESTEUERTE FADENGRAFIKEN

Das Modellieren von natürlichen Abläufen mit dem Computer ist nicht nur ein Spiel, sondern hat vielseitige Anwendungen. Mit dem Computer kannst du in viel kürzerer Zeit und mit viel weniger Aufwand verschiedene Situationen durchtesten, bis du eine gefunden hast, die du dann in die Praxis umsetzen willst. Dein Programm ist dann besonders attraktiv, wenn du mit der Maus Veränderungen vornehmen kannst, die sich sofort auswirken. Durch die Verwendung von Callbacks ist dies in Python mit wenig zusätzlichem Aufwand verbunden.

Du kannst in deinem Programm den Eckpunkt A mit einer Mausbewegung verschieben und die Fadengrafik wird unmittelbar neu erstellt.

Dazu verwendest du zum Erstellen der Grafik in die Funktion updateGraphics(), die von den Maus-Callbacks aufgerufen wird. Dabei löschst du jeweils das ganze Grafikfenster und erstellst es neu mit dem Punkt A an der aktuellen Lage des Mauscursors

from gpanel import *

def updateGraphics():
    clear()
    line(pA, pB)
    line(pA, pC)
    r = 0
    while r <= 1:
        pX1 = getDividingPoint(pA, pB, r)
        pX2 = getDividingPoint(pA, pC, 1 - r)
        line(pX1, pX2)
        r += 0.05

def myCallback(x, y):
    pA[0] = x
    pA[1] = y
    updateGraphics()

makeGPanel(0, 100, 0, 100, 
              mousePressed = myCallback,
              mouseDragged = myCallback)

pA = [10, 10]
pB = [90, 20]
pC = [30, 90]
updateGraphics()

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Du kannst auch zwei verschiedene Events, hier den Press-Event und den Drag-Event mit demselben Callback abhandeln.

AUFGABEN

Erstelle die nebenstehende Fadengrafik

Ergänze die Fadengrafik von Aufgabe 1 derart, dass du mit einem Maus-Drag die Dreiecksspitze ziehen kannst und die Grafik dabei immer wieder neu gezeichnet wird.

ZUSATZSTOFF

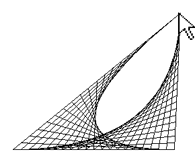
BÉZIER-KURVEN

Diese Kurven wurden in den sechziger Jahren des letzten Jahrhunderts von Pierre Bézier, damals Ingenieur beim Automobilkonzern Renault, erfunden, um ästhetisch wohlgeformte Kurven für den Design von Industrieprodukten zu erzeugen.

Du kannst eine kubische Bézier-Kurve mit dem Algorithmus von de Casteljau als Fadengrafik erzeugen.

Der Algorithmus lautet wie folgt:

	Du gibst dir 4 Punkte P0, P1, P2, P3 vor. (P0 und P3 werden die Endpunkte der Kurve sein, P1 und P2 nennt man die Kontrollpunkte).
	Verbinde P0P1, P1P2, P2P3
	Teile die Strecken P0P1, P1P2, P2P3 in äquidistante Teilungspunkte ein. Für ein bestimmtes Teilverhältnis gibt dies die Teilungspunkte Q1, Q2, Q3.
	Verbinde Q1Q2, Q2Q3
	Teile die Strecken Q1Q2, Q2Q3 im selben Teilverhältnis. Dies gibt dies die Teilungspunkte R2 und R3
	Verbinde R2R3

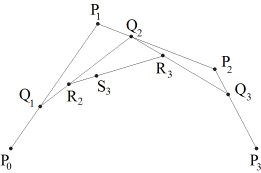
Du kannst den Algorithmus einfach in einem Programm implementieren, wenn du Punkte als Listen implementierst und die Funktion getDividingPoint() mehrmals aufrufst.

from gpanel import *

makeGPanel(0, 100, 0, 100)
     
pt1 = [10, 10]
pc1 = [20, 90]
pc2 = [70, 70]
pt2 = [90, 20]

setColor("green")

line(pt1, pc1)
line(pt2, pc2)
line(pc1, pc2)

r = 0
while r <= 1:
    q1 = getDividingPoint(pt1, pc1, r)
    q2 = getDividingPoint(pc1, pc2, r)
    q3 = getDividingPoint(pc2, pt2, r)
    line(q1, q2)
    line(q2, q3)
    r2 = getDividingPoint(q1, q2, r)
    r3 = getDividingPoint(q2, q3, r)
    line(r2, r3)
    r += 0.05

setColor("black")
#cubicBezier(pt1, pc1, pc2, pt2)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Eine kubische Bézier-Kurve ist durch 4 Punkte bestimmt. In GPanel kannst du sie mit der Funktion cubicBezier() zeichnen. Es werden die aktuelle Zeichnungsfarbe und Liniendicke verwendet.

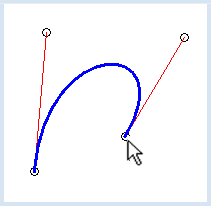
INTERAKTIVER KURVENDESIGN

Kombinierst du deine Kenntnisse, so kannst du bereits ein ziemlich professionelles Programm schreiben, mit dem du ein Bézierkurve erzeugen und durch Ziehen mit der Maus interaktiv verändern kannst. Das Programm merkt sogar, wenn du mit dem Mauscursor in der Nähe eines der 4 Punkte bist und färbt diesen. Mit einem Press-Event kannst du dann diesen Punkt packen und ziehen.

Die vier Punkte müssen im Programm mehrmals durchlaufen werden. Es ist darum zweckmässig, dass du sie auch in eine Liste mit dem Namen points steckst, die du dann mit einer for-Struktur bearbeiten kannst.

Wichtig ist auch, dass du weisst, welchen der Punkte du gerade gepackt hast. Diese Information speicherst du in einer Variable active : sie hat den Wert -1, falls keiner der Punkte gepackt ist, sonst entspricht ihr Wert dem Index des betreffenden Punkts.

from gpanel import *

def updateGraphics():
    # erase all
    clear()
 
    # draw points
    lineWidth(1)
    for i in range(4):
        move(points[i])
        if active == i:
            setColor("green")
            fillCircle(2)
        setColor("black")
        circle(2)

    # draw tangents
    setColor("red")
    line(points[0], points[1])
    line(points[3], points[2])

    # draw Bezier curve
    setColor("blue")
    lineWidth(3)
    cubicBezier(points[0], points[1], points[2], points[3])

def onMouseDragged(x, y):
    if active == -1:
        return
    points[active][0] = x
    points[active][1] = y
    updateGraphics()

def onMouseReleased(x, y):
    active = -1
    updateGraphics()

def onMouseMoved(x, y):
    global active
    active = near(x, y)
    updateGraphics()

def near(x, y):
    for i in range(4):
        rsquare = (x - points[i][0]) * (x - points[i][0]) + 
                     (y - points[i][1]) * (y - points[i][1])
        if rsquare < 4:
            return i
    return -1        

pt1 = [20, 20]
pc1 = [10, 80]
pc2 = [90, 80]
pt2 = [80, 20]
points = [pt1, pc1, pc2, pt2]
active = -1

makeGPanel(0, 100, 0, 100,
    mouseDragged = onMouseDragged,
    mouseReleased = onMouseReleased,
    mouseMoved = onMouseMoved)
updateGraphics()

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

MEMO

Es gibt auch kompliziertere Datenstrukturen, wie beispielsweise eine Liste, deren Elemente wieder Listen sind. Willst du beispielsweise die x-Koordinate von P1 ansprechen, so verwendest du points[1][0], also ein doppeltes Klammerpaar.

Heute sind die Bézierkurven ein wichtiges Designhilfsmittel im CAD-Bereich. [Lit.]

AUFGABEN

Das Herz besteht aus zwei kubischen Bézier-Kurven mit gleichen Anfangs- und Endpunkten sowie symmetrischen Kontrollpunkten. Skizziere auf einem Blatt Papier, wo diese Punkte etwa liegen könnten und erstelle dann die Grafik. Das Füllen erfolgt mit der Funktion fill(punkt, alte_farbe, neue_farbe), wo punkt ein innerer Punkt eines umrandeten Gebiets ist.