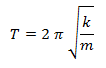Forum
3.13 WIDGETS
![]()
EINFÜHRUNG |
|
Dir bekannte Programme besitzen meist eine grafische Benutzeroberfläche, ein GUI (Graphics User Interface). Du erkennst gewöhnlich eine Menüleiste, Eingabefelder und Schaltflächen (Buttons). GUI-Komponenten, auch Widgets genannt, werden als Objekte aufgefasst, so wie du sie aus dem Kapitel Turtleobjekte bereits kennst. Willst du Programme mit einer modernen Benutzeroberfläche schreiben, so ist es darum unumgänglich, dass du die grundlegenden Konzepte der Objektorientierten Programmierung (OOP) kennst [mehr...Die Konzepte der OOP werden vertieft im Kapitel Spielprogrammierung behandelt]. Die Widgets werden in verschiedene Klassen gemäss folgende Liste eingeteilt:
So wie du eine Turtle mit dem Aufruf des Konstruktors der Klasse Turtle erzeugt hast, musst du eine GUI-Komponente durch den Aufruf des entsprechenden Klassenkonstruktors erzeugen. Oft besitzen die Konstruktoren Parameter, mit denen du bestimmte Eigenschaften des Widgets festlegen kannst. Beispielsweise erzeugst du ein Eingabefeld der Länge 10 Zeichen mit tf = JTextField(10). Beim Aufruf des Konstruktors wir auch eine Variable definiert, mit der du nachher auf das Objekts zugreifst. Beispielsweise liefert tf.getText() den Text, der im Textfeld steht. Um ein Widget in einem GPanel sichtbar zu machen, verwendest du die Funktion addComponent() und übergibst ihr die Objektvariable. Dabei werden die Widgets automatisch in der Reihenfolge der Aufrufe im oberen Teil des GPanel-Fensters plaziert [mehr...Für ein allgemeineres Layout müsste man einen Layout-Manager verwenden, was später behandelt wird]. |
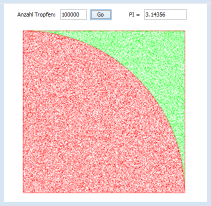
π MIT DER REGENTROPFEN-SIMULATION |
Das GUI besteht aus zwei Labels, zwei Textfeldern und einem Button. Nach ihrer Erzeugung fügst du sie mit addComponent() ins GPanel ein. Es versteht sich von selbst, dass das Klicken auf den OK-Button als Event aufgefasst wird. Der Callback wird über den benannten Parameter actionListener im Konstruktor von JButton registriert. Du hast sicher nicht vergessen, dass du in einem Callback keinen lang dauernden Code ausführen solltest. Darum rufst du im Callback lediglich wakeUp() auf, wodurch das mit putSleep() in der while-Schleife angehaltene Programm aufgeweckt wird und es die Simulation ausführt. from gpanel import * from random import random from javax.swing import * def actionCallback(e): wakeUp() def createGUI(): addComponent(lbl1) addComponent(tf1) addComponent(btn1) addComponent(lbl2) addComponent(tf2) validate() def init(): tf2.setText("") clear() move(0.5, 0.5) rectangle(1, 1) move(0, 0) arc(1, 0, 90) def doIt(n): hits = 0 for i in range(n): zx = random() zy = random() if zx * zx + zy * zy < 1: hits = hits + 1 setColor("red") else: setColor("green") point(zx, zy) return hits lbl1 = JLabel("Number of drops: ") lbl2 = JLabel(" PI = ") tf1 = JTextField(6) tf2 = JTextField(10) btn1 = JButton("OK", actionListener = actionCallback) makeGPanel("Monte Carlo Simulation", -0.1, 1.1, -0.1, 1.1) createGUI() tf1.setText("10000") init() while True: putSleep() init() n = int(tf1.getText()) k = doIt(n) pi = 4 * k / n tf2.setText(str(pi)) |
MEMO |
|
Widgets sind Objekte der Swing-Klassenbibliothek. Sie werden mit dem Konstruktor, der den Namen der Klasse hat, erzeugt. Beim Aufruf des Konstruktors wird eine Variable definiert, mit der du auf das Objekt zugreifen kannst. Um das Widget im GPanel anzuzeigen, rufst du die Funktion addComponent() auf und übergibst ihr die Widget-Variable. Nachdem du alle Widgets zum GPanel hinzugefügt hast, solltest du validate() aufrufen, damit das Fenster mit Sicherheit mit den eingefügten Widgets neu aufgebaut wird. Button-Callbacks kannst du mit dem benannten Parameter actionListener registrieren. Denke daran, dass ein Callback nie lange dauernden Code ausführen sollte. |
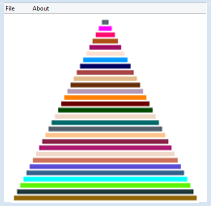
MENÜS (Nichts zum Essen) |
Viele Bildschirmfester besitzen eine Menüleiste mit mehreren Menüeinträgen (Items). Beim Klicken auf einen Menüeintrag, kann auch ein Untermenü geöffnet werden, das wiederum Menüeinträge enthält. Menüs und Menüobjekte werden ebenfalls als Objekte aufgefasst. Die Auswahl einer Menüoption löst einen Event aus, der über einen Callback behandelt wird.
from gpanel import * from javax.swing import * def actionCallback(e): if e.getSource() == goItem: wakeUp() if e.getSource() == exitItem: dispose() if e.getSource() == aboutItem: msgDlg("Pyramides Version 1.0") def doIt(): clear() for i in range(1, 30): setColor(getRandomX11Color()) fillRectangle(i/2, i - 0.35, 30 - i/2, i + 0.35) fileMenu = JMenu("File") goItem = JMenuItem("Go", actionPerformed = actionCallback) exitItem = JMenuItem("Exit", actionPerformed = actionCallback) fileMenu.add(goItem) fileMenu.add(exitItem) aboutItem = JMenuItem("About", actionPerformed = actionCallback) menuBar = JMenuBar() menuBar.add(fileMenu) menuBar.add(aboutItem) makeGPanel(menuBar, 0, 30, 0, 30) while not isDisposed(): putSleep() if not isDisposed(): doIt() |
MEMO |
|
Du hältst dich an die Regel, dass in Callbacks kein lange dauernder Code ausgeführt werden soll. Du führst das Zeichnen also im Hauptblock durch. Damit das Programm mit Sicherheit beendet wird, wenn du den Close-Button des Fensters oder die Exit-Option klickst, testest du mit isDisposed(), ob das Fenster geschlossen wurde [mehr...Beim Schiessen des Fensters bzw. beim Aufruf von dispose() wird automatisch putSleep() verlassen]. |
EIN SEPARATES DIALOGFENSTER BENUTZEN |
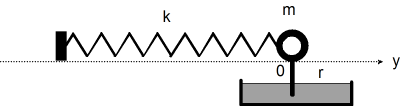
TigerJython stellt dir Werkzeuge zur Verfügung, mit denen sich eigenständige Dialogfenster ohne viel Aufwand realisieren lassen. Dabei werden die klassischen Bedienungselemente wie Textfelder, Schaltflächen (Buttons), Markierungsfelder (Checkboxen), Optionsfelder (Radiobuttons) und Schieberegler (Sliders) als Python-Objekte modelliert, die sich in Bereichen (Panes) eines Bildschirmfensters befinden, das während der Programmausführung ständig sichtbar bleibt. Ein solches Fenster nennt man auch einen nicht-modalen Dialog. Das Dialogfenster wird durch ein Objekt der Klasse EntryDialog() erzeugt, wo die einzelnen Bereiche als Objekte der Klasse EntryPane() in der Reihenfolge der Parameter untereinander eingefügt sind. Die EntryPanes enthalten die Bedienungselemente als Objekte der Klassen ButtonEntry, RadioEntry, CheckEntry, IntEntry, FloatEntry, LongEntry, StringEntry und SliderEntry. (Du kannst dich in der APLU-Dokumentation genauer orientieren.) Dein Programm simuliert die Bewegung einer Masse, die an einer Feder befestigt ist und eine geschwindigkeitsproportionale Reibung erfährt. Es könnte sich um die Aufhängung eines Autorads handeln, das mit einem Stossdämpfer versehen ist.
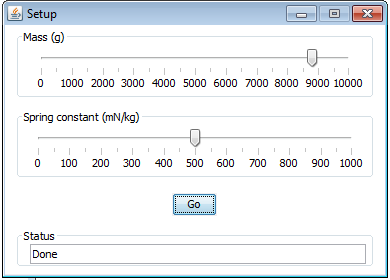
Gemäss dem Newtonschen Bewegungsgesetz berechnet sich die Beschleunigung aus a = F/m, wo F die Kraft und m die Masse sind. Das Feder- und das Reibungsgesetz liefern F = -k*x - r*v, wo k die Federkonstante und r der Reibungskoeffizient sind. Die Lösung erfolgt iterativ in kleinen Zeitschritten dt: Die neue Geschwindigkeit ist v = v + a*dt und die neue y-Koordinate y = y + v*dt. Du verwendest ein Dialogfenster mit einem Schieberegler für den Reibungskoeffizenten, einer Statuszeile, um Rückmeldungen an den Benutzer zu geben, und einem Start-Button, um die Simulation zu starten. Es werden drei Objekte friction, status und btn erzeugt, die du je in eine EntryPane pane1, pane2, pane3 fügst. Diese übergibst du dem EntryDialog, der sie in der Parameterreihenfolge darstellt.
from gpanel import * import math def doIt(): clear() drawGrid(0, 200, -100, 100, "seagreen") m = mass.getValue() / 1000 # Mass (kg) k = spring.getValue() / 1000 # Spring const (N/kg) t = 0; y = 50; v = 0 # Initial conditions r = 0.7 # Coefficient of friction (N/m/s) d = 200; dt = 0.01 status.setValue("m = %6.2f kg, k = %6.2f N/kg" % (m, k)) move(t, y) # Initial cursor position while t < d: draw(t, y) # Draw segment F = -k*y - r*v # Force a = F/m # Acceleration v = v + a*dt # New velocity y = y + v*dt # New position t = t + dt # New time T = 2 * math.pi * math.sqrt(m / k) status.setValue("Done") mass = SliderEntry(0, 10000, 10000, 1000, 500) pane1 = EntryPane("Mass (g)", mass) spring = SliderEntry(0, 1000, 500, 100, 50) pane2 = EntryPane("Spring constant (mN/kg)", spring) goBtn = ButtonEntry("Go") pane3 = EntryPane(goBtn) status = StringEntry("") pane4 = EntryPane("Status", status) dlg = EntryDialog(850, 150, pane1, pane2, pane3, pane4) makeGPanel() window(-20, 220, -110, 110) drawGrid(0, 200, -100, 100, "seagreen") title("Harmonic Oscillation") status.setValue("Press Go to start") while not dlg.isDisposed(): if isDisposed(): dlg.dispose() break if goBtn.isTouched(): doIt() dispose() |
MEMO |
Damit das Programm bei Klicken auf den Close-Button der Titelleiste beendet wird, verwendest du in einer while-Schleife die Bedingung isDisposed(), die wahr wird, sobald der Close-Button gedrückt wird. In doIt() frägst die den Zustand der Bedienungselemente mit getValue() ab. Mit isTouched() findest du heraus, ob du mit der Maus auf ein Bedienungselement geklickt hast, hier zum Beispiel auf den Start-Button. Durch einige Versuche findest du heraus, dass sich die Schwingungsdauer mit zunehmender Dämpfung wenig ändert und dass es einen Grenzfall gibt, wo keine Schwingung mehr auftritt. Dieser asymptotische Grenzfall wird bei Stossdämpfern von Autos angewendet, damit das Auto möglichst wenig schwingt. |
AUFGABEN |
|