Forum
3.10 ZUFALL
![]()
EINFÜHRUNG |
|
Im täglichen Leben spielen Zufälle eine grosse Rolle. Man versteht darunter Ereignisse, die nicht voraussehbar sind. Bittet man dich etwa, aus den Farben rot, grün und blau eine Farbe zu wählen, so kann niemand voraussagen, für welche du dich entscheidest, die Farbe ist also zufällig. Auch bei Games spielt der Zufall eine grosse Rolle: Wirft du einen Würfel, so ist die Augenzahl zwischen 1 und 6 zufällig. Obschon die Welt vom Zufall regiert wird [mehr...
Die Naturgesetze werden mit der Quantentheorie Für Zufallsexperimente ist der Computer hervorragend geeignet, da es sehr einfach ist, eine grosse Anzahl von Versuchen durchzuführen. Dazu muss der Computer eine Reihe von Zufallszahlen erzeugen, die möglichst voneinander unabhängig sind. Man verwendet meist Ganzzahlen in einem gewissen vorgegebenen Bereich, z.B. zwischen 1 und 6, oder Dezimalzahlen zwischen 0 und 1. Einen Algorithmus, der eine Reihe von Zufallszahlen berechnet, nennt man einen Zufallszahlengenerator. Es ist wichtig, dass die Zahlen mit gleicher Häufigkeit auftreten, wie man es von einem (nicht gezinkten) Würfel her gewohnt ist. Man nennt solche Zahlen gleichverteilt [mehr... Da ein Computer nach streng determinierten Regeln arbeitet, sind die Zahlen eigentlich vorhersehbar. Man spricht deswegen von Pseudozufallszahlen]. |
ZUFÄLLIGES MALEN |
from gpanel import * from random import randint, random def randomColor(): r = randint(0, 255) g = randint(0, 255) b = randint(0, 255) return makeColor(r, g, b) makeGPanel() bgColor(randomColor()) for i in range(20): setColor(randomColor()) move(random(), random()) a = random() / 2 b = random() / 2 fillEllipse(a, b) |
MEMO |
|
random() liefert gleichverteilte Zufallszahlen als Float zwischen 0 (eingeschlossen) und 1 (ausgeschlossen). Du musst das Modul random importieren, um darauf zugreifen zu können. Mit randint(start, end) erhält man eine ganzzahlige Zufallszahl zwischen start und end (beide eingeschlossen). Farben werden durch ihren Rot-, Grün- und Blauanteil (RGB) festgelegt. Die Werte sind Ganzahlen zwischen 0 und 255. Die Funktion makeColor() liefert aus den 3 Farbwerten für Rot, Grün und Blau ein Farbobjekt. |
HÄUFIGKEIT VON WÜRFELZAHLEN |
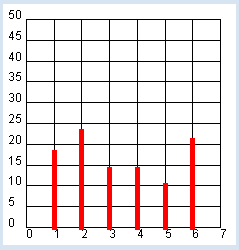
from gpanel import * from random import randint NB_ROLLS = 100 makeGPanel(-1, 8, -0.1 * NB_ROLLS / 2, 1.1 * NB_ROLLS / 2) title("# Rolls: " + str(NB_ROLLS)) drawGrid(0, 7, 0, NB_ROLLS // 2, 7, 10) setColor("red") histo = [0, 0, 0, 0, 0, 0, 0] # hist = [0] * 7 # short form for i in range(NB_ROLLS): pip = randint(1, 6) histo[pip] += 1 lineWidth(5) for n in range(1, 7): line(n, 0, n, histo[n]) |
MEMO |
|
Die Häufigkeit, mit der die einzelnen Augenzahlen (pip) vorkommen, müssen gespeichert werden. Du verwendest dazu die Liste histo, in der du die Vorkommnisse beim entsprechenden Index aufsummierst. Du benötigst eine Liste mit 7 Elementen, da der Index von 1 bis 6 läuft. Wie du durch einige Experimente feststellen kannst, sind die Häufigkeiten bei grösser werdenden Wurfzahlen NB_ROLLS immer besser ausgeglichen und erreichen immer genauer 1/6 der Wurfzahl. Diese Tatsache drückt man so aus: Die Wahrscheinlichkeit, beim Würfelwerfen eine der Augenzahlen zu erhalten, ist 1/6. Für das Koordinatengitter rufst du drawGrid(xmin, xmax, ymin, ymax, xticks, yticks) mit 6 Parametern auf. Die zwei letzten Parameter bestimmen die Anzahl der Unterteilungen. Ist xmax oder ymax ein Float so erfolgt die Achsenbeschriftung ebenfalls in Floats, sonst sind es Integer. |
MONTE-CARLO-SIMULATION |
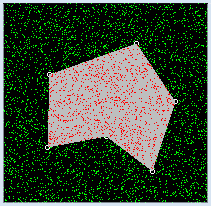
Das Fürstentum Monaco ist durch sein Casino im Stadtteil Monte-Carlo weltberühmt. Das Casino hat nicht nur seit 150 Jahren eine magische Anziehungskraft auf Berühmtheiten, sondern auch auf Mathematiker, die versuchen, die Spiele zu analysieren und Gewinnstrategien zu entwickeln. Zum Test der Strategien eignet sich der Computer besser als das reale Spiel, da man bei Computerexperimenten kein Geld verliert. Beim folgenden "Spiel" wirfst du Punkte auf eine quadratische Fläche, auf der ein Polygon liegt. Die Punkte kannst du anschaulich auch als Regentropfen auffassen. Wie dies beim Regen üblich ist, fallen in einer gewissen Zeit ungefähr immer gleich viel Tropen auf jede Flächeneinheit. Die Tropfen sind also gleichverteilt. Du lässt eine bestimmte totale Zahl von Regentropfen fallen und zählst, wie viele davon auf die Polygonfläche fallen. Es ist offensichtlich, dass diese Zahl mit zunehmendem Flächeninhalt des Polygons zunimmt und im Mittel proportional zum Flächeninhalt ist. Beispielsweise fallen auf ein Polygon mit einem Flächeninhalt von ¼ des Flächeninhalts des umgebenden Quadrats ja wohl (im Mittel) ¼ aller Regentropfen. Aus dieser Erkenntnis kannst du nun umgekehrt durch Zählen der Tropfen den Flächeninhalt herausfinden. Ist das nicht elegant?
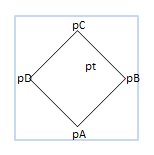
from gpanel import * from random import random NB_DROPS = 10000 def onMousePressed(x, y): if isLeftMouseButton(): pt = [x, y] move(pt) circle(0.5) corners.append(pt) if isRightMouseButton(): wakeUp() def go(): global nbHit setColor("gray") fillPolygon(corners) setStatusText("Working. Please wait...") for i in range(NB_DROPS): pt = [100 * random(), 100 * random()] color = getPixelColorStr(pt) if color == "black": setColor("green") point(pt) if color == "gray" or color == "red": nbHit += 1 setColor("red") point(pt) setStatusText("All done. #hits: " + str(nbHit) + " of " + str(NB_DROPS)) makeGPanel(0, 100, 0, 100, mousePressed = onMousePressed) addStatusBar(30) setStatusText("Select corners with left button. Start dropping with right button") bgColor("black") setColor("white") corners = [] nbHit = 0 putSleep() go() |
MEMO |
Beim Klicken der linken Maustaste speicherst du die Eckpunkte des Polygons in einer Liste corners und zeichnest als Markierung kleine Kreise. Die eigentliche Regensimulation wird in der Funktion go() durchgeführt. Sie beginnt beim Klicken der rechten Maustaste und dauerst eine gewisse Zeit. Dabei machst du mit verschieden farbigen Punkten die fallenden Regentropfen sichtbar. Rufst du, wie es eigentlich auf der Hand liegt, go() im pressCallback() direkt auf, so siehst du nichts, bis die Simulation zu Ende ist. Das System unterbindet nämlich aus systeminternen Gründen das Auffrischen der Grafik in einem Maus-Callback. Willst du also in einem Callback eine länger dauernde Aktion sichtbar machen, so muss dies in einem anderen Teil des Programms geschehen. Oft wird der Hauptblock des Programms dazu verwendet. Die Ausführung wird mit putSleep() vorübergehend angehalten. Der Press-Event weckt das schlafende Hauptprogramm mit wakeUp() auf und dieses führt nun die Simulation mit dem Aufruf von go() aus. Um Schwierigkeiten zu vermeiden, solltest du dich in Zukunft unbedingt an das folgende Prinzip halten: Callbacks müssen immer rasch zurückkehren. Es dürfen darin keine lange dauernde Aktionen ausgeführt werden. Um herauszufinden, ob ein Regentropfen auf die grau gefärbte Polygonfläche gefallen ist, wendest du folgenden Trick an: Du holt dir mit getPixelColorStr() die Farbe der Auftreffstelle. Ist die Farbe grau (oder rot, wenn bereits ein anderer Tropf dort hingefallen ist), so erhöhst du nbHit um 1 und färbst die Stelle rot. Du kannst das Verfahren testen, indem du einige einfache Polygone (z.B. Rechtecke, Dreiecke) erzeugst und mit dem Massstab den Bildschirm ausmisst. Du erkennst dann, dass es sehr viele Regentropfen braucht, um ein einigermassen exaktes Resultat zu erhalten [mehr...
Es gilt etwa: Für 1 Kommastelle bessere Genauigkeit (Faktor 10), |
CHAOS-SPIEL |
Es ist auf den ersten Blick erstaunlich, dass sich mit Zufallsexperimenten regelmässige Muster erzeugen lassen. Dies hängt damit zusammen, dass sich die statistischen Schwankungen bei grossen Zahlen ausgleichen. [mehr...
Obschon die zu Grund liegenden Naturgesetze auf der Quantentheorie basieren 1. Konstruiere ein gleichseitiges Dreieck mit den Ecken A, B, C
from gpanel import * from random import randint MAXITERATIONS = 100000 makeGPanel(0, 10, 0, 10) pA = [1, 1] pB = [9, 1] pC = [5, 8] triangle(pA, pB, pC) corners = [pA, pB, pC] pt = [2, 2] title("Working...") for iter in range(MAXITERATIONS): i = randint(0, 2) pRand = corners[i] pt = getDividingPoint(pRand, pt, 0.5) point(pt) title("Working...Done") |
MEMO |
Benötigst du ein zufälliges Objekt, so fügst du alle Objekte in eine Liste und holst mit einem zufälligen Index eines davon heraus. Es ist erstaunlich, dass du mit zufällig gewählten Punkten eine regelmässige Figur, nämlich ein Sierpinski-Fraktal, erzeugen kannst. |
AUFGABEN |
|