deutsch     english     français     Drucken

 

3.12 BILDER DRUCKEN

 

 

EINFÜHRUNG

 

Du hast bereits im Kapitel Turtlegrafik die Turtle auf einem Drucker hochauflösend zeichnen lassen. Gleichartig kannst du ein Bild von GPanel auf dem Drucker rendern. Du kannst auch einen virtuellen Drucker verwenden, der eine Grafik-Datei in einem hochauflösenden Format (z.B. Tiff oder EPS) erstellt [mehr...Unter Windows eignet sich beispielsweise ImagePrinter]. Dazu definierst du eine parameterlose Funktion mit irgend einem Namen, beispielsweise doIt(),  die alle Befehle zur Erstellung des Bildes enthält. Beim direkten Aufruf erscheint das Bild auf dem Bildschirm. Um es auszudrucken, rufst du printerPlot(doIt)  auf. Du kannst auch noch einen Skalierungsfaktor k angeben, also printerPlot(doIt, k) aufrufen. Für k < 1 ergibt sich eine Verkleinerung, für k > 1 eine Vergrösserung.

PROGRAMMIERKONZEPTE: Hochauflösende Grafik

 

 

ROSETTEN

 

Die rosenartigen Kurven gehen auf dem Mathematiker Guido Grandi aus dem 18. Jahrhundert zurück [mehr... Sie werden auch Rhodonea-Kurven genannt]
Die erzeugende Funktion lässt sich am einfachsten in Polarkoordinaten (ρ, φ) ausdrücken. Sie besitzt einen Parameter n
                  ρ = sin(nφ) 
Die kartesischen Koordinaten erhält man wie üblich aus

                  x =  ρ cos(φ)
                  y =  ρ sin(φ)

Eine hübsche Rosette erhältst du mit n = . Auf einem Drucker sieht sie aber noch viel schöner aus als auf dem Bildschirm.

  

 

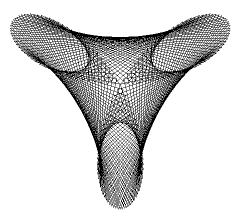
from gpanel import *
import math
  
def rho(phi):
    return math.sin(n * phi)

def doIt():
    phi = 0
    while phi < nbTurns * math.pi:
        r = rho(phi)
        x = r * math.cos(phi)    
        y = r * math.sin(phi)    
        if phi == 0:
          move(x, y)
        else:
          draw(x, y)
        phi += dphi

n = math.sqrt(2)
dphi = 0.01
nbTurns = 100
makeGPanel(-1.2, 1.2, -1.2, 1.2)
doIt()
printerPlot(doIt)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Je nach der Wahl des Parameters n kannst du ganz verschiedenartige Kurven erzeugen. Versuche es mit natürlichen Zahlen, mit rationalen Zahlen (Brüchen) und mit irrationalen Zahlen (π, e).

 

 

MAURER-ROSEN

 

Der Mathematiker Peter Maurer hat diese Kurven 1987 in seinem Artikel "A Rose is a Rose..." eingeführt. Sie verwenden die Rosetten als "Leitlinie". Auf dieser Leitlinie wählst immer nach einem bestimmten Drehwinkel d insgesamt 360 Punkte. Nachher verbindest du diese Punkt mit Geradenstücken.

Je nach Wahl von n und d ergeben sich ganz unterschiedliche Kurvengebilde. Ausgedruckt wirken diese noch viel schöner (hier für n = 3 und d = 47 Grad).

  

 

from gpanel import *
import math

def sin(x):
    return math.sin(math.radians(x))

def cos(x):
    return math.cos(math.radians(x))

def cartesian(polar):
    return [polar[0] * cos(polar[1]), polar[0] * sin(polar[1])]         

def rho(phi):
    return sin(n * phi)

def doIt():
    for i in range(361):
        k = i * d
        pt = [rho(k), k]
        corners.append(pt)    
        
    move(cartesian(corners[0]))    
    for pt in corners:
        draw(cartesian(pt))
  
corners = []
n = 3
d = 47
makeGPanel(-1.2, 1.2, -1.2, 1.2)
doIt()
printerPlot(doIt)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Im Programm verwendest du Grad- und nicht Bogenmass. Darum ist es günstig, deine eigenen Funktionen für Sinus und Cosinus zu definieren, die mit Grad rechnen. Dies vereinfacht auch die Schreibweise, da du nicht immer math. davor schreiben musst.

Ebenso ist es günstig, eine Umrechnung von Polar- auf kartesische Koordinaten in der Funktion cartesian() vorzunehmen, wo die Koordinatenpaare als Liste verpackt sind.
Die Polarkoordinaten der 361 Punkte, die du auf der Leitlinie auswählst, speicherst du in der Liste corners. Am Ende durchläufst du diese und ziehst mit draw() Linien von Punkt zu Punkt.

Bekannte andere Maurer-Rosen kannst du mit folgenden Parametern zeichnen:

n
d
2
39
2
31
6
71

 

 

AUFGABEN

 
1.

Zeichne mit der Funktion wave(center, wavelength) 50 konzentrische Kreise mit center als Mittelpunkt und wavelength als Radiusinkrement. Man kann das Bild als Wellenberge einer Kreiswelle auffassen. Zeichne die Welle mit wenig verschobenen Mittelpunkt und beobachte auf einem Ausdruck das entstehende Interferenzbild. Welche aus der Geometrie bekannte Kurve erkennst du?