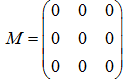Forum
8.9 GRUPPENDYNAMIK
![]()
EINFÜHRUNG |
Systeme mit vielen Partnern, die aufeinander einwirken, sind weit verbreitet. Computerprogramme können solche Systeme oft mit erstaunlich wenig Aufwand simulieren, da der Computer den Zustand von Tausenden, ja Millionen von Einzelindividuen speichern und zeitlich verfolgen kann. Handelt es sich aber um atomare Vielteilchensysteme mit einer Teilchenzahl in der Grössenordnung von 1023, so stösst auch der Computer an seine Grenzen. Zur Simulation solcher Systeme müssen vereinfachende Verfahren eingesetzt werden, etwa indem man das System in einzelne grössere Zellen einteilt. Beispiele dafür sind die Simulation der Erdatmosphäre für die Wetterprognose und die Voraussage der langfristigen Klimaentwicklung. |
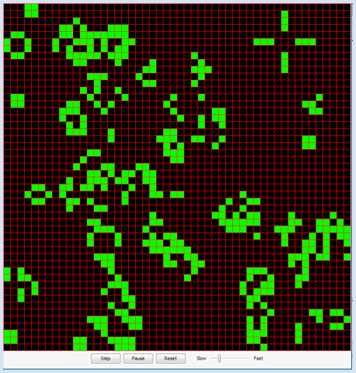
CONWAY'S GAME OF LIFE |
Beim Übergang zur nächsten Generation wird der aktuelle Zustand festgehalten und der Nachfolgezustand jeder Zelle auf Grund ihrer 8 nächsten Nachbarn mit folgenden vier Übergangsregeln bestimmt:
Die Zellenstruktur von GameGrid ist ideal, um das Spiel zu implementieren. Für die Population verwendest du eine zweidimensionale Liste a[x][y] mit den Werten 0 für eine tote und 1 für eine lebende Zelle. Der Simulationszyklus wird als Generationszyklus aufgefasst und im Callback onAct() die aktuelle Population von der Liste a in die neue Population b umkopiert, die am Schluss als die aktuelle Liste angesehen wird. Im Callback onReset(), der beim Klick auf den Reset-Button aufgerufen wird, wählst du 1000 zufällige lebende Zellen. Um die Callbacks zu aktivieren, musst du sie mit registerAct() bzw. registerNavigation() registrieren. from gamegrid import * def onReset(): for x in range(s): for y in range(s): a[x][y] = 0 # All cells dead for n in range(z): loc = getRandomEmptyLocation() a[loc.x][loc.y] = 1 showPopulation() def showPopulation(): for x in range(s): for y in range(s): loc = Location(x, y) if a[x][y] == 1: getBg().fillCell(loc, Color.green, False) else: getBg().fillCell(loc, Color.black, False) refresh() def getNumberOfNeighbours(x, y): nb = 0 for i in range(max(0, x - 1), min(s, x + 2)): for k in range(max(0, y - 1), min(s, y + 2)): if not (i == x and k == y): if a[i][k] == 1: nb = nb + 1 return nb def onAct(): global a # Don't use the current, but a new population b = [[0 for x in range(s)] for y in range(s)] for x in range(s): for y in range(s): nb = getNumberOfNeighbours(x, y) if a[x][y] == 1: # living cell if nb < 2: b[x][y] = 0 elif nb > 3: b[x][y] = 0 else: b[x][y] = 1 else: # dead cell if nb == 3: b[x][y] = 1 else: b[x][y] = 0 a = b # Use new population as current showPopulation() # =================== global section ================== s = 50 # Number of cells in each direction z = 1000 # Size of population at start a = [[0 for x in range(s)] for y in range(s)] makeGameGrid(s, s, 800 // s, Color.red) registerAct(onAct) registerNavigation(resetted = onReset) setTitle("Conway's Game Of Life") onReset() show() |
MEMO |
Das Game of Live ist ein Beispiel eines zellulären Automaten, der aus Gitterzellen besteht, die miteinander wechselwirken. Sie sind hervorragend geeignet, um das Verhalten komplexer natürlicher Systeme zu untersuchen. Beispiele:
Der Wissenschaftler und Chefentwickler von Mathematica Stefan Wolfram hat 2002 in seinem bekannten Buch "A New Kind of Science" darauf hingewiesen, dass solche Systeme mit einfachen Programmen untersucht werden können und wir mit der Computercomputersimulation am Anfang einer neuen Ära stehen, wissenschaftliche Erkenntnisse zu gewinnen. Bei der Initialisierung der zweidimensionalen Liste wird eine spezielle Python-Syntax mit der Bezeichnung List Comprehension verwendet (siehe Zusatzstoff). |
SCHWARMVERHALTEN |
Wie du aus dem täglichen Leben weisst, haben grosse Gruppen von Lebewesen oft die Tendenz, sich in Gruppen zusammenzuschliessen. Dies ist besonders gut bei Vögeln, Fischen und Insekten zu beobachten. Aber auch demonstrierende Menschen zeigen dieses "Schwarmverhalten". Für die Bildung eines Schwarms spielen einerseits äussere (globale) Einflüsse, aber auch die Wechselwirkung zwischen Partnern in der näheren Umgebung, also lokale Einflüsse, eine Rolle. Craig Reynolds hat 1986 gezeigt, dass folgende drei Regeln zu einer Schwarmbildung zwischen Individuen (er nannte sie Boids) führen:
Für die Implementierung verwendest du wieder GameGrid, um den Aufwand für die Animation klein zu halten. Es ist zweckmässig, ein Gitter mit Pixelgrösse zu verwenden und den Ort, die Geschwindigkeit und die Beschleunigung der Actors mit Float-Vektoren aus der Klasse GGVector anzugeben. In jeder Simulationsperiode bestimmst du zuerst mit setAcceleration() den neuen Beschleunigungsvektor gemäss der drei Regeln. Daraus ergeben sich der neue Geschwindigkeits- und Ortsvektor aus
Da die absolute Zeitskala unwesentlich ist, kannst du für den Zeitschritt dt = 1 setzen. Bei der Anwendung der Separationsregel führen nicht nur nahe fliegende Vögel zu einer Abstossung, sondern auch Hindernisse (hier die Bäume). Der Rand des Flugbereichs (die Wand) muss besonders behandelt werden. Dazu stehen verschiedene Möglichkeiten zur Auswahl. Es könnte eine torusartige Topologie verwendet werden, wo die auf der einen Seite aus dem Bereich hinausfliegenden Vögel auf der gegenüberliegenden Seite wieder hineinfliegen. Hier werden die Vögel gezwungen, am Rand umzukehren. from gamegrid import * import math from random import randint # =================== class Tree ======================= class Tree(Actor): def __init__(self): Actor.__init__(self, "sprites/tree1.png") # =================== class Bird ======================= class Bird(Actor): def __init__(self): Actor.__init__(self, True, "sprites/arrow1.png") self.r = GGVector(0, 0) # Position self.v = GGVector(0, 0) # Velocity self.a = GGVector(0, 0) # Acceleration # Called when actor is added to gamegrid def reset(self): self.r.x = self.getX() self.r.y = self.getY() self.v.x = startVelocity * math.cos(math.radians(self.getDirection())) self.v.y = startVelocity * math.sin(math.radians(self.getDirection())) # ----------- cohesion --------------- def cohesion(self, distance): return self.getCenterOfMass(distance).sub(self.r) # ----------- alignment -------------- def alignment(self, distance): align = self.getAverageVelocity(distance) align = align.sub(self.v) return align # ----------- separation ------------- def separation(self, distance): repulse = GGVector() # ------ from birds ------ for p in birdPositions: dist = p.sub(self.r) d = dist.magnitude() if d < distance and d != 0: repulse = repulse.add(dist.mult((d - distance) / d)) # ------ from trees ------ trees = self.gameGrid.getActors(Tree) for actor in trees: p = GGVector(actor.getX(), actor.getY()) dist = p.sub(self.r) d = dist.magnitude() if d < distance and d != 0: repulse = repulse.add(dist.mult((d - distance) / d)) return repulse # ----------- wall interaction ------- def wallInteraction(self): width = self.gameGrid.getWidth() height = self.gameGrid.getHeight() acc = GGVector() if self.r.x < wallDist: distFactor = (wallDist - self.r.x) / wallDist acc = GGVector(wallWeight * distFactor, 0) if width - self.r.x < wallDist: distFactor = ((width - self.r.x) - wallDist) / wallDist acc = GGVector(wallWeight * distFactor, 0) if self.r.y < wallDist: distFactor = (wallDist - self.r.y) / wallDist acc = GGVector(0, wallWeight * distFactor) if height - self.r.y < wallDist: distFactor = ((height - self.r.y) - wallDist) / wallDist acc = GGVector(0, wallWeight * distFactor) return acc def getPosition(self): return self.r def getVelocity(self): return self.v def getCenterOfMass(self, distance): center = GGVector() count = 0 for p in birdPositions: dist = p.sub(self.r) d = dist.magnitude() if d < distance: center = center.add(p) count += 1 if count != 0: return center.mult(1.0/count) else: return center def getAverageVelocity(self, distance): avg = GGVector() count = 0 for i in range(len(birdPositions)): p = birdPositions[i] if (self.r.x - p.x) * (self.r.x - p.x) + \ (self.r.y - p.y) * (self.r.y - p.y) < distance * distance: avg = avg.add(birdVelocities[i]); count += 1 return avg.mult(1.0/count) def limitSpeed(self): m = self.v.magnitude() if m < minSpeed: self.v = self.v.mult(minSpeed / m) if m > maxSpeed: self.v = self.v.mult(minSpeed / m) def setAcceleration(self): self.a = self.cohesion(cohesionDist).mult(cohesionWeight) self.a = self.a.add(self.separation(separationDist).mult(separationWeight)) self.a = self.a.add(self.alignment(alignmentDist).mult(alignmentWeight)) self.a = self.a.add(self.wallInteraction()) def act(self): self.setAcceleration() self.v = self.v.add(self.a) # new velocity self.limitSpeed() self.r = self.r.add(self.v) # new position self.setDirection(int(math.degrees(self.v.getDirection()))) self.setLocation(Location(int(self.r.x), int(self.r.y))) # =================== global section ================== def populateTrees(number): blockSize = 70 treesPerBlock = 10 for block in range(number // treesPerBlock): x = getRandomNumber(800 // blockSize) * blockSize y = getRandomNumber(600 // blockSize) * blockSize for t in range(treesPerBlock): dx = getRandomNumber(blockSize) dy = getRandomNumber(blockSize) addActor(Tree(), Location(x + dx, y + dy)) def generateBirds(number): for i in range(number): addActorNoRefresh(Bird(), getRandomLocation(), getRandomDirection()) onAct() # Initialize birdPositions, birdVelocities def onAct(): global birdPositions, birdVelocities # Update bird positions and velocities birdPositions = [] birdVelocities = [] for b in getActors(Bird): birdPositions.append(b.getPosition()) birdVelocities.append(b.getVelocity()) def getRandomNumber(limit): return randint(0, limit-1) # coupling constants cohesionDist = 100 cohesionWeight = 0.01 alignmentDist = 30 alignmentWeight = 1 separationDist = 30 separationWeight = 0.2 wallDist = 20 wallWeight = 2 maxSpeed = 20 minSpeed = 10 startVelocity = 10 numberTrees = 100 numberBirds = 50 birdPositions = [] birdVelocities = [] makeGameGrid(800, 600, 1, False) registerAct(onAct) setSimulationPeriod(10) setBgColor(makeColor(25, 121, 212)) setTitle("Swarm Simulation") show() populateTrees(numberTrees) generateBirds(numberBirds) doRun() |
MEMO |
Die Simulation ist von verschiedenen Kopplungskonstanten abhängig, welche die "Stärke" der Wechselwirkung bestimmen. Ihre Werte sind sehr sensibel und du musst sie eventuell an die Leistungsfähigkeit deines Computers anpassen. Wiederum wird der Callback onAct() mit registerAct() aktiviert, damit er automatisch in jedem Simulationszyklus aufgerufen wird. In der Methode act() der Klasse Bird werden die Vögel bewegt. |
AUFGABEN |
|
ZUSATZSTOFF |
LIST COMPREHENSION |
|
Im Python können Listen elegant mit einer speziellen Schreibweise erzeugt werden. Sie lehnt sich an die mathematische Notation aus der Mengenlehre an.
Verwende die Konsole, um die Python-Ausdrücke auszutesten. Du kannst sie aus der Tabelle kopieren und in die Konsole einfügen.
|