Forum
8.7 KOMPLEXE ZAHLEN & FRAKTALE
![]()
EINFÜHRUNG |
Komplexe Zahlen sind in der Mathematik von grosser Wichtigkeit, da sie die Menge der reellen Zahlen so erweitern, dass viele Sätze einfacher und allgemeiner formuliert werden können. Sie spielen darüber hinaus in Naturwissenschaften und Technik eine wichtige Rolle, insbesondere in der Physik und Elektrotechnik [mehr...
Die Quantentheorie spielt sich gänzlich in der Welt der komplexen Komplexe Zahlen können in der Gaussschen Zahlenebene als Zeiger oder als Punkte dargestellt werden. Damit sich auch ein Turtlefenster, ein GPanel und eine Pixelgitter von JGameGrid als Gausssche Zahlenebene auffassen lassen, stehen in den entsprechenden Bibliotheken alle Funktionen mit Koordinatenparametern (x, y) auch direkt für komplexe Zahlen zur Verfügung. |
GRUNDOPERATIONEN MIT KOMPLEXEN ZAHLEN |
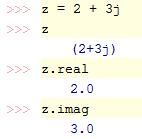
In Python verwendest du für die imaginäre Einheit an Stelle von i das in der Elektrotechnik übliche Symbol j. Du kannst die komplexe Zahl mit Realteil 2 und Imaginärteil 3 auf mehrere Arten definieren:
Verwende für die folgenden Beispiele die praktische TigerJython-Konsole.
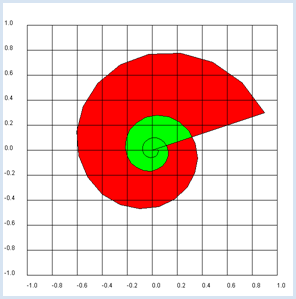
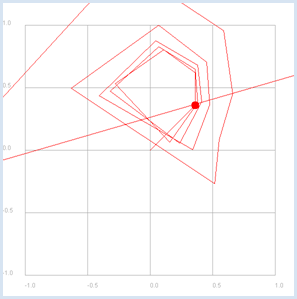
from gpanel import * makeGPanel(-1.2, 1.2, -1.2, 1.2) title("Complex plane") z = 0.9 + 0.3j for n in range(1, 60): y = z**n draw(y) fill(0.2, 0, "white", "red") fill(0.0, 0.2, "white", "green") drawGrid(-1.0, 1.0, -1.0, 1.0)
|
MEMO |
|
draw(z) bewirkt das gleiche wie draw(z.real, z.imag), ist aber einfacher. Du verwendest GPanel-Koordinaten, die auf allen Seiten 10% grösser als der verwendete Koordinatenbereich ist. In drawGrid() musst du die Koordinaten als Float angeben, damit das Gitter mit Floats angeschrieben wird. |
KONFORME ABBILDUNGEN |
Bei zweidimensionalen Abbildungen wird jedem Punkt P(x, y) ein Bildpunkt P'(x', y') zugeordnet.
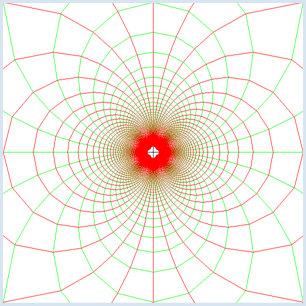
from gpanel import * # function f(z) = 1/z def f(z): if z == 0: return 0 return 1 / z min_value = -5.0 max_value = 5.0 step = 1 / 20 reStep = complex(step, 0) imStep = complex(0, step) makeGPanel(min_value, max_value, min_value, max_value) title("Conformal mapping for f(z) = 1 / z") line(min_value, 0, max_value, 0) # Real axis line(0, min_value, 0, max_value) # Imaginary axis # Transform horizontal line per line setColor("green") z = complex(min_value, min_value) while z.imag < max_value: z = complex(min_value, z.imag) # left move(f(z)) while z.real < max_value: # move along horz. line draw(f(z)) z = z + reStep z = z + imStep # Transform vertical line per line setColor("red") z = complex(min_value, min_value) while z.real < max_value: z = complex(z.real, min_value) # bottom move(f(z)) while z.imag < max_value: # move along vert. line draw(f(z)) z = z + imStep z = z + reStep
|
MEMO |
|
Wie du aus der Grafik entnimmst, schneiden sich die Bilder der Gitterlinien wieder rechtwinklig. Eine Abbildung, bei der der Winkel zwischen sich schneidenden Linien erhalten bleibt, nennt man winkeltreu und man spricht von einer konformen Abbildung [mehr... Man kann natürlich mathematisch exakt beweisen, dass die Inversion eine konforme Abbildung ist] . |
MANDELBROT-FRAKTALE |
Um Mandelbrot-Fraktale zu erstellen, betrachtest du zu der vorgegebenen komplexen Zahl c eine (rekursiv definierte) Folge von komplexen Zahlen nach dem Bildungsgesetz:
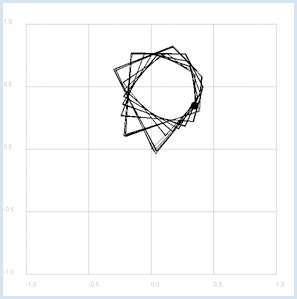
Falls der Betrag der Folgenglieder in einem beschränkten Bereich bleibt, also nicht über alle Grenzen wächst, gehört c zur Mandelbrot-Menge. Um dich mit dem Algorithmus vertraut zu machen, zeichnest du die Folgenglieder für zwei komplexe Zahlen c1 = 0.35 + 0.35j und c2 = 0.36 + 0.36j. Dabei siehst du sofort, dass c1 zur Mandelbrot-Menge gehört, c2 hingegen nicht.
from gpanel import * def f(z): return z * z + c makeGPanel(-1.2, 1.2, -1.2, 1.2) title("Mandelbrot iteration") drawGrid(-1, 1.0, -1, 1.0, 4, 4, "gray") isMandelbrot = askYesNo("c in Mandelbrot set?") if isMandelbrot: c = 0.35 + 0.35j setColor("black") else: c = 0.36+ 0.36j setColor("red") title("Mandelbrot iteration with c = " + str(c)) move(c) fillCircle(0.03) z = 0j while True: if z == 0: move(z) else: draw(z) z = f(z) delay(100)
from gpanel import * def isInSet(c): z = 0 for n in range(maxIterations): z = z*z + c if abs(z) > R: # diverging return False return True maxIterations = 50 R = 2 xmin = -2 xmax = 1 xstep = 0.03 ymin = -1.5 ymax = 1.5 ystep = 0.03 makeGPanel(xmin, xmax, ymin, ymax) line(xmin, 0, xmax, 0) # real axis line(0, ymin, 0, ymax) # imaginary axis title("Mandelbrot set") y = ymin while y <= ymax: x = xmin while x <= xmax: c = x + y*1j inSet = isInSet(c) if inSet: move(c) fillCircle(0.01) x += xstep y += ystep
from gpanel import * def getIterationColor(it): color = makeColor((30 * it) % 256, (4 * it) % 256, (255 - (30 * it)) % 256) return color def mandelbrot(c): z = 0 for it in range(maxIterations): z = z*z + c if abs(z) > R: # diverging return it return maxIterations maxIterations = 50 R = 2 xmin = -2 xmax = 1 xstep = 0.003 ymin = -1.5 ymax = 1.5 ystep = 0.003 makeGPanel(xmin, xmax, ymin, ymax) title("Mandelbrot set") enableRepaint(False) y = ymin while y <= ymax: x = xmin while x <= xmax: c = x + y*1j itCount = mandelbrot(c) if itCount == maxIterations: # inside Mandelbrot set setColor("black") else: # outside Mandelbrot set setColor(getIterationColor(itCount)) point(c) x += xstep y += ystep repaint() |
MEMO |
|
Um das Zeichnen etwas zu beschleunigen, wird enableRepaint(False) gesetzt und nur am Ende jeder Zeile mit repaint() neu gerendert. Das Mandelbrot-Fraktal besitzt die bemerkenswerte Eigenschaft, dass bei einer Vergrösserung eines Ausschnitts wieder eine ähnliche Struktur erscheint [mehr... Allerdings ist die Struktur nicht exakt gleich und damit ist das Fraktal nicht strikt selbstähnlich] . |
AUFGABEN |
|
ZUSATZSTOFF |
WECHSELSTROM UND IMPEDANZ |
Elektrische Schaltungen für sinusförmige Wechselspannungen und Wechselströmen, die aus passiven Bauelementen (Widerständen, Kondensatoren, Spulen) aufgebaut sind, können wie Gleichstromschaltungen behandelt werden, wenn du für Spannungen, Ströme und Widerstände komplexe Grössen verwendest. Ein allgemeiner komplexer Widerstand heisst auch Impedanz und wird oft mit Z und für rein imaginäre Widerstände mit X bezeichnet. Die Impedanz eines ohmschen Widerstands ist R, einer Spule XL = jωL (L: Induktivität) und eines Kondensators XC = 1 / jωC (C: Kapazität), wobei ω = 2πf (f: Frequenz) ist. Eine komplexe Wechselspannung u = u(t) läuft in der Gaussschen Zahlenebene gleichförmig auf einem Kreis. Wird sie an eine Impedanz Z angelegt, so fliesst der Strom i(t) und nach dem Ohmschen Gesetz gilt u = Z * i. Da bei der Multiplikation von komplexen Zahlen die Phasen addiert und die Beträgt multipliziert werden, läuft u um die Phase von Z phasenverschoben vor i
Also läuft i auch auf einem Kreis. Für die Beträge (Amplituden) gilt:
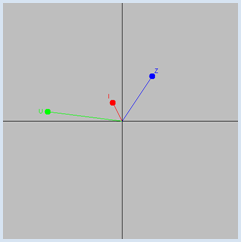
from gpanel import * import math def drawAxis(): line(min, 0, max, 0) # real axis line(0, min, 0, max) # imaginary axis def cdraw(z, color, label): oldColor = setColor(color) line(0j, z) fillCircle(0.2) z1 = z + 0.5 * z / abs(z) - (0.1 + 0.2j) text(z1, label) setColor(oldColor) min = -10 max = 10 dt = 0.001 makeGPanel(min, max, min, max) enableRepaint(False) bgColor("gray") title("Complex voltages and currents") f = 10 # Frequency omega = 2 * math.pi * f t = 0 uA = 5 Z = 2 + 3j while True: u = uA * (math.cos(omega * t) + 1j * math.sin(omega * t)) i = u / Z clear() drawAxis() cdraw(u, "green", "U") cdraw(i, "red", "I") cdraw(Z, "blue", "Z") repaint() t += dt delay(100)
|
MEMO |
|
Elektrische Schaltungen mit passiven Bauelementen lassen wie Gleichstromschaltungen behandeln, wenn man Spannung, Strom und Widerstand als komplexe Zahlen auffasst. |
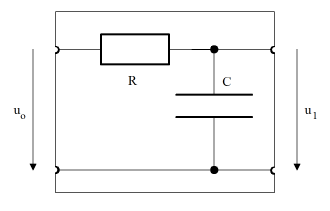
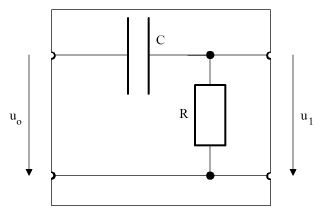
Die Berechnung ist einfach: Für die Serieschaltung von R und C ergibt sich die Impedanz Z = R + XC und damit der Strom i = uo / Z, also wiederum mit dem Ohmschen Gesetz die Ausgangspannung
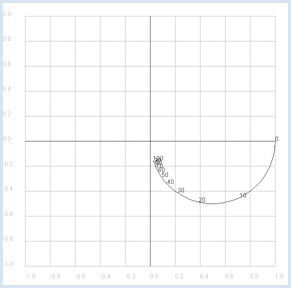
from gpanel import * from math import pi def drawAxis(): line(-1, 0, 1, 0) # Real axis line(0, -1, 0, 1) # Imaginary axis makeGPanel(-1.2, 1.2, -1.2, 1.2) drawGrid(-1.0, 1.0, -1.0, 1.0, "gray") setColor("black") drawAxis() title("Complex gain factor – low pass") R = 10 C = 0.001 def v(f): if f == 0: return 1 + 0j omega = 2 * pi * f XC = 1 / (1j * omega * C) return XC / (R + XC) f = 0 # Frequency while f <= 100: if f == 0: move(v(f)) else: draw(v(f)) if f % 10 == 0: text(str(f)) f += 1 delay(10) Im Bode-Plot wird der Verstärkungsfaktor nach Betrag und Phase aufgeteilt und in Funktion der Frequenz aufgetragen (üblich sind allerdings logarithmische Skalen).
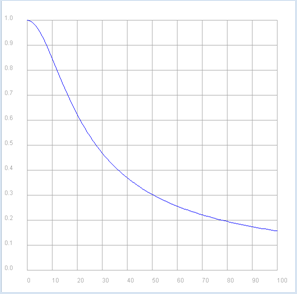
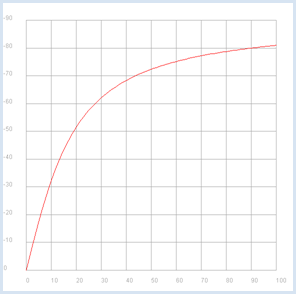
from gpanel import * import math import cmath R = 10 C = 0.001 def v(f): if f == 0: return 1 + 0j omega = 2 * math.pi * f XC = 1 / (1j * omega * C) return XC / (R + XC) p1 = GPanel(-10, 110, -0.1, 1.1) drawPanelGrid(p1, 0, 100, 0, 1.0, "gray") p1.title("Bode Plot - Low Pass, Gain") p1.setColor("blue") f = 0 while f <= 100: if f == 0: p1.move(f, abs(v(f))) else: p1.draw(f, abs(v(f))) f += 1 p2 = GPanel(-10, 110, 9, -99) drawPanelGrid(p2, 0, 100, 0, -90, 10, 9, "gray") p2.title("Bode Plot - Low Pass, Phase") p2.setColor("red") f = 0 while f <= 100: if f == 0: p2.move(f, math.degrees(cmath.phase(v(f)))) else: p2.draw(f, math.degrees(cmath.phase(v(f)))) f += 1 |
MEMO |
|
Im Bode-Plot wird nochmals besonders deutlich, dass die vorliegende Schaltung tiefe Frequenzen gut und hohe Frequenzen schlecht überträgt. Zwischen Eingang- und Ausgangssignal besteht zudem eine Phasenverschiebung im Bereich 0 bis -90 Grad. Man sagt, dass die Ausgangsspannung der Eingangsspannung "nachhinkt" bzw. dass die Eingangsspannung der Ausgangsspannung "vorausläuft". |
AUFGABEN |
|