deutsch     english     français     Drucken

 

8.6 KORRELATION, REGRESSION

 

 

EINFÜHRUNG

 

In den Naturwissenschaften, aber auch im täglichen Lebens spielt die Erfassung von Daten in Form von Messgrössen eine wichtige Rolle. Dabei braucht aber nicht immer ein Messinstrument  zum Einsatz zu kommen. Es kann sich beispielsweise auch um Umfragewerte im Zusammenhang mit einer statistischen Untersuchung handeln. Nach der Datenerfassung geht es meist darum, die Messwerte zu interpretieren. Es kann sich um qualitative Aussagen handeln, beispielsweise dass die Messwerte im Laufe der Zeit ansteigen oder absinken, aber auch um die experimentelle Überprüfung eines Naturgesetzes.

Ein grosses Problem besteht darin, dass Messungen fast immer Schwankungen ausgesetzt und nicht exakt reproduzierbar sind. Trotz dieses "Messfehlern" möchte man wissenschaftlich korrekte Aussagen machen können. Die Messfehler entstehen dabei nicht immer wegen mangelhaften Messgeräten, sondern können in der Natur des Experiments liegen. So liefert die "Messung" der Augenzahl eines geworfenen Würfels grundsätzlich streuende Werte zwischen 1 und 6. Bei jeder Art von Messung spielen darum statistische Überlegungen eine zentrale Rolle.

Oft werden in einer Messserie zwei Grössen x und y miteinander gemessen und man stellt sich die Frage, ob diese in einem Zusammenhang stehen und einer Gesetzmässigkeit unterworfen sind. Trägt man die (x, y)-Werte als Messpunkte in ein Koordinatensystem ein, so spricht man von Datenvisualisierung. Fast immer erkennt man bei blosser Betrachtung der Verteilung der Messwerte, ob die Daten in einer gegenseitigen Abhängigkeit stehen.

PROGRAMMIERKONZEPTE:
Datenvisualisierung, Messwertverteilung, Wolkendiagramm, Rauschen, Kovarianz, Korrelationskoeffizient, Regression, Bester Fit

 

 

UNABHÄNGIGE UND ABHÄNGIGE DATEN VISUALISIEREN

 


Du kannst leicht in einem x-y-Diagramm unabhängige Daten simulieren, indem du für x und y gleichverteilte Zufallszahlen verwendest. Obschon es hier nicht nötig ist, kopierst du die Messwerte in die Datenlisten xval und yval und stellst sie erst danach als Datenpunkte dar.

   


from random import random
from gpanel import *

z = 10000
    
makeGPanel(-1, 11, -1, 11)
title("Uuniformly distributed value pairs")
drawGrid(10, 10, "gray")

xval = [0] * z
yval = [0] * z

for i in range(z):
    xval[i] = 10 * random()
    yval[i] = 10 * random()
    move(xval[i], yval[i])
    fillCircle(0.03)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Galaxienähnliche Grafiken erhältst du, falls die x- und y-Werte zwar immer noch unabhängig voneinander sind, aber ihre Verteilung um einen Mittelwert normalverteilt ist. Hier wird als Mittelwert 5 und als Streuung 1 verwendet. Man spricht auch von einem Scatter Plot oder Wolkendiagramm.

Mit der Funktion random.gauss(mittelwert, streuung) kannst du sehr einfach normalverteilte Zufallszahlen erzeugen.

   

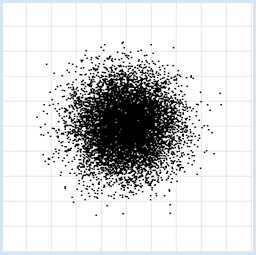
from random import gauss
from gpanel import *

z = 10000
    
makeGPanel(-1, 11, -1, 11)
title("Normally distributed value pairs")
drawGrid(10, 10, "gray")

xval = [0] * z
yval = [0] * z

for i in range(z):
    xval[i] = gauss(5, 1)
    yval[i] = gauss(5, 1)
    move(xval[i], yval[i])
    fillCircle(0.03)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Abhängigkeiten zwischen x- und y-Werten kannst du so simulieren, dass x in einem bestimmten Bereich in äquidistanten Schritten ansteigt und y eine Funktion von x ist, die aber statistischen Schwankungen unterworfen ist. Solche Schwankungen nennt man in der Physik auch Rauschen.

Du zeichnest das Wolkendiagramm für eine Parabel y = -x * (0.2 * x - 2) und normalverteiltem Rauschen im Bereich x = 0..10 mit einer Schrittweite von 0.01.

   

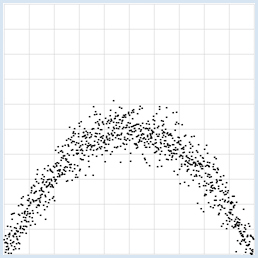
from random import gauss
from gpanel import *
import math

z = 1000
a = 0.2
b = 2

def f(x):
    y = -x * (a * x - b)
    return y

makeGPanel(-1, 11, -1, 11)
title("y = -x * (0.2 * x - 2) with normally distributed noise")
drawGrid(0, 10, 0, 10, "gray")

xval = [0] * z
yval = [0] * z

for i in range(z):
    x = i / 100
    xval[i] = x
    yval[i] = f(x) + gauss(0, 0.5)
    move(xval[i], yval[i])
    fillCircle(0.03)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Durch Datenvisualisierung erkennt man gegenseitige Abhängigkeiten von Messgrössen auf den ersten Blick [mehr... Dieses Beispiel ist dadurch berühmt, weil die unten eingeführte Korrelation die Abhängigkeit nicht erkennt].

Bei im Intervall [a, b] gleichverteilten Zufallszahlen kommen die Zahlen in jedem gleichlangen Teilintervall mit gleicher Häufigkeit vor. Normalverteilte Zahlen haben eine glöckenförmige Verteilung, wobei 68% der Zahlen im Intervall (Mittelwert - Streuung) und (Mittelwert + Streuung) liegen.

 

 

KOVARIANZ ALS MASSZAHL FÜR ABHÄNGIGKEITEN

 

Hier geht es darum, gegenseitige Abhängigkeiten nicht nur in einem Diagramm sichtbar zu machen, sondern auch durch eine Zahl auszudrücken. Wie schon oft, gehts du von einem konkreten Beispiel aus und betrachtest den Doppelwurf von Würfeln, wobei vorerst x die Augenzahl des ersten und y die Augenzahl des zweiten Würfels sind. Du führst das Wurfexperiment oftmals aus und zeichnest die Wertepaare als Wolkendiagramm. Da die beiden Messwerte x und y unabhängig sind, ergibt sich eine regelmässige Punktwolke. Berechnest du die Erwartungswerte von x und y, so ergibt sich bekanntlich 3.5.

  

Da x und y unabhängig, gilt für die Wahrscheinlichkeit pxy, beim Doppelwurf das Paar x, y zu erhalten pxy = px * py.

Die Vermutung liegt nahe, dass allgemein die folgende Produktregel gilt.

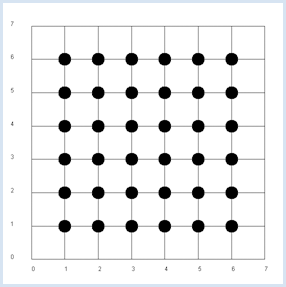
Sind x und y unabhängig, so ist der Erwartungswert von x*y gleich dem Produkt der Erwartungswerte von x und y [mehr... Der theoretische Beweis ist einfach:

] .

In der Simulation wird diese Vermutung bestätigt. 

from random import randint
from gpanel import *

z = 10000 # number of double rolls

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

makeGPanel(-1, 8, -1, 8)
title("Double rolls. Independent random variables")
addStatusBar(30)
drawGrid(0, 7, 0, 7, 7, 7, "gray")

xval =  [0] * z
yval =  [0] * z
xyval = [0] * z

for i in range(z):
    a = randint(1, 6)
    b = randint(1, 6)
    xval[i] = a
    yval[i] = b
    xyval[i] = xval[i] * yval[i]
    move(xval[i], yval[i])
    fillCircle(0.2)

xm = mean(xval)
ym = mean(yval)
xym = mean(xyval)
setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  E(x, y) = " + dec2(xym))
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 
 

MEMO

 

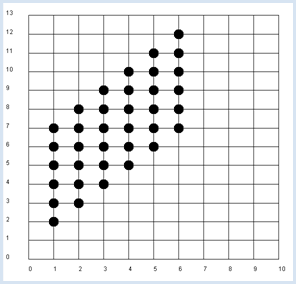
Es ist zweckmässig, eine Statusbar zu verwenden, um die Resultate auszuschreiben. Die Funktion dec2() rundet die Werte auf 2 Stellen und gibt sie als String ab.

Die Werte unterliegen natürlich einer statistischen Schwankung.

In der nächsten Simulation untersuchst du nicht mehr die geworfenen Augenpaare, sondern die Augenzahl x des ersten Würfels und die Summe y der beiden Augenzahlen. Es ist offensichtlich, dass nun y in einer Abhängigkeit von x ist, denn wenn beispielsweise x = 1 ist, so ist die Wahrscheinlichkeit für y = 4 nicht dieselbe wie wenn x = 2 ist.

 

Deine Simulation bestätigt, dass die Produktregel tatsächlich nicht mehr gilt, falls x und y voneinander abhängig sind. Es liegt daher nahe, die Abweichung von der Produktregel, also die Differenz

c = E(x*y) - E(x)*E(y)

Kovarianz genannt,  als Mass für die Abhängigkeit von x und y einzuführen. Gleichzeitig siehst du in deinem Programm, dass die Kovarianz auch als Summe der quadratischen Abweichungen vom Mittelwert berechnet werden kann.

   

from random import randint
from gpanel import *

z = 10000 # number of double rolls

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n
    
makeGPanel(-1, 11, -2, 14)
title("Double rolls. Independent random variables")
addStatusBar(30)
drawGrid(0, 10, 0, 13, 10, 13, "gray")

xval =  [0] * z
yval =  [0] * z
xyval = [0] * z

for i in range(z):
    a = randint(1, 6)
    b = randint(1, 6)
    xval[i] = a
    yval[i] = a + b
    xyval[i] = xval[i] * yval[i]
    move(xval[i], yval[i])
    fillCircle(0.2)

xm = mean(xval)
ym = mean(yval)
xym = mean(xyval)
c = xym - xm * ym
setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  E(x, y) = " + dec2(xym) + \
          ",  c = " + dec2(c) + \
          ",  covariance = " + dec2(covariance(xval, yval)))
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Du erhältst in der Simulation für die Kovarianz den Wert von ungefähr 2.9. Die Kovarianz eignet sich also sehr wohl als Mass für die Abhängigkeit von Zufallsvariablen.

 

 

DER KORRELATIONSKOEFFIZIENT

 

Die eben eingeführte Kovarianz hat noch einen Nachteil. Je nachdem wie die Messgrössen x und y skaliert sind, ergeben sich andere Werte, auch wenn die Werte offenbar gleichermassen voneinander abhängig sind. Du kannst dies leicht einsehen. Nimmst du beispielsweise zwei Würfel, die statt der Augenzahlen 1, 2,...,6 die Augenzahlen 10, 20,...,60 haben, so ändert sich die Kovarianz stark, obschon die Abhängigkeit dieselbe ist. Aus diesem Grund hat führt man eine normierte Kovarianz ein, die man Korrelationskoeffizient nennt, indem man die Kovarianz durch die Streuungen der x und y-Werte dividiert:

  Korrelationskoeffizient(x, y) = (         Kovarianz(x, y)        )/ Streuung(x) * Streuung(y)  

Der Korrelationskoeffizient bleibt immer im Bereich -1 bis 1. Ein Wert nahe bei 0 entspricht einer kleinen Abhängigkeit, ein Wert nahe bei 1 einer grossen Abhängigkeit, wobei zunehmende Werte von x zunehmenden Werte von y entsprechen, für  einen Wert nahe bei -1 entsprechen zunehmende Werte von x abnehmenden Werten von y.

Im Programm verwendest du wieder den Doppelwurf und untersuchst die Abhängigkeit der Summe der Augenzahlen von der Augenzahl des ersten Würfels.

 

from random import randint
from gpanel import *
import math

z = 10000 # number of double rolls
k = 10 # scalefactor

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval) / (deviation(xval) * deviation(yval))
    
makeGPanel(-1 * k, 11 * k, -2 * k, 14 * k)
title("Double rolls. Independent random variables.")
addStatusBar(30)
drawGrid(0, 10 * k, 0, 13 * k, 10, 13, "gray")

xval =  [0] * z
yval =  [0] * z
xyval = [0] * z

for i in range(z):
    a = k * randint(1, 6)
    b = k * randint(1, 6)
    xval[i] = a
    yval[i] = a + b
    xyval[i] = xval[i] * yval[i]
    move(xval[i], yval[i])
    fillCircle(0.2 * k)

xm = mean(xval)
ym = mean(yval)
xym = mean(xyval)
c = xym - xm * ym
setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  E(x, y) = " + dec2(xym) + \
          ",  covariance = " + dec2(covariance(xval, yval)) + \
          ",  correlation = " + dec2(correlation(xval, yval)))
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 
 

MEMO

 

Du kannst den Skalenfaktor k verändern und der Korrelationskoeffzient bleibt immer ungefähr 0.71, hingegen ändert sich die Kovarianz stark [mehr... Der Korrelationskoeffizient prüft eigentlich nur lineare Abhängigkeiten. Wendest du ihn beispielsweise
auf das oben genannte parabelförmige Wolkendiagramm an, so ergibt sich ein Wert
nahe bei 0, obschon die Werte offensichtlich zusammenhängen].

Statt Korrelationskoeffizient sagt man auch  nur kurz Korrelation.

 

 

MEDIZINWISSENSCHAFTLICHE PUBLIKATION

 

Mit deinen bisherigen Kenntnissen bist du bereits in der Lage, eine wissenschaftlichen Publikation, die im Jahr 2012 in der renommierten Zeitschrift "New England Journal of Medicine" erschienen ist, [mehr... F. H. Messerli, Chocolate Comsumption, Cognitive Function, and Nobel Laureates,
The New England Journal of Medicine 367;16 (Oct. 2012)] zu verstehen und zu beurteilen. Dabei wird der Zusammenhang zwischen dem Schokoladekonsum und der Zahl der Nobelpreisträger in verschiedenen Industriestaaten untersucht, oder anders gesagt, wird der Frage nachgegangen, ob es einen Zusammenhang zwischen Schokoladeessen und Intelligenz gibt. Im Artikel geht der Autor von folgenden Datenquellen aus, die du auch selbst im Internet findet:

  

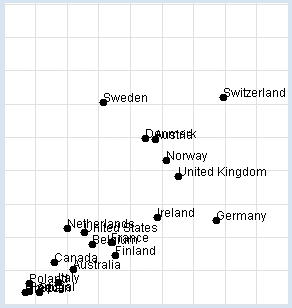
Nobelpreise:
http://en.wikipedia.org/wiki/List_of_countries_by_Nobel_laureates_per_capita

Schokoladekonsum:
http://www.chocosuisse.ch/web/chocosuisse/en/documentation/facts_figures.html
http://www.theobroma-cacao.de/wissen/wirtschaft/international/konsum

Du willst die Untersuchung selbst nachvollziehen. In deinem Programm verwendest du für den Ländernamen, den Schokoladekonsum in kg pro Jahr und Einwohner und die Zahl der Nobelpreisträger pro 10 Millionen Einwohner eine Liste data mit Teillisten aus drei Elementen. Im Programm stellst du die Daten grafisch dar und bestimmst den Korrelationskoeffizienten.

from gpanel import *
import math

data = [["Australia", 4.8, 5.141],
        ["Austria", 8.7, 24.720],
        ["Belgium", 5.7, 9.005],
        ["Canada", 3.9, 6.253],
        ["Denmark", 8.2, 24.915],
        ["Finland", 6.8, 7.371],
        ["France", 6.6, 9.177],
        ["Germany", 11.6, 12.572],
        ["Greece", 2.5, 1.797],
        ["Italy", 4.1, 3.279],
        ["Ireland", 8.8, 12.967],
        ["Netherlands", 4.5, 11.337],
        ["Norway", 9.2, 21.614],
        ["Poland", 2.7, 3.140],
        ["Portugal", 2.7, 1.885],
        ["Spain", 3.2, 1.705],
        ["Sweden", 6.2, 30.300],
        ["Switzerland", 11.9, 30.949],
        ["United Kingdom", 9.8, 19.165],
        ["United States", 5.3, 10.811]]

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval) / (deviation(xval) * deviation(yval))

makeGPanel(-2, 17, -5, 55)
drawGrid(0, 15, 0, 50, "lightgray")

xval = []
yval = []

for country in data:
    d = country[1]
    v = country[2]
    xval.append(d)
    yval.append(v)   
    move(d, v)
    fillCircle(0.2)
    text(country[0])

title("Chocolate-Brainpower-Correlation: " + dec2(correlation(xval, yval)))
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 
 

MEMO

 

Es ergibt sich eine hohe Korrelation von ungefähr 0.71, die man auf verschiedene Arten interpretieren kann. Richtig ist es zu sagen, dass es einen Zusammenhang zwischen den beiden Datenreihen gibt, allerdings lässt sich über den Grund nur spekulieren. Insbesondere ist damit ein kausaler Zusammenhang zwischen Schokoladekonsum und Intelligenz keineswegs nachgewiesen. Grundsätzlich gilt: Bei einer hohen Korrelation zwischen x und y kann die Grösse x die Ursache für das Verhalten von y sein. Ebenso kann die Grösse y die Ursache für das Verhalten von x sein, oder x und y mit anderen gemeinsamen, vielleicht sogar unbekannten Ursachen im Zusammenhang stehen.

Diskutiere Sinn und Zweck dieser Untersuchung auch mit Personen aus deinem Umfeld und frage sie nach ihrer Meinung.

 

 

MESSFEHLER UND RAUSCHEN

 

Selbst bei einem exakten Zusammenhang zwischen x und y können Messfehler oder andere Einflüsse zu schwankenden Messwerten führen. In dieser Simulation gehst du von einem linearen Zusammenhang zwischen x und y aus, wobei aber die Funktionswerte y normalverteilten Schwankungen unterworfen werden.

Du bestimmst den Korrelationskoeffizienten und zeichnest den Punkt mit den Koordinaten (xm, ym) ein, wo xm bzw. ym die Erwartungswerte von x und y sind.

 

   

from random import gauss
from gpanel import *
import math

z = 1000
a = 0.6
b = 2
sigma = 1

def f(x):
    y = a * x + b
    return y

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval) / (deviation(xval) * deviation(yval))
    
makeGPanel(-1, 11, -1, 11)
title("y = 0.6 * x + 2 normally distributed measurement errors")
addStatusBar(30)
drawGrid(0, 10, 0, 10, "gray")
setColor("blue")
lineWidth(3)
line(0, f(0), 10, f(10))

xval = [0] * z
yval = [0] * z

setColor("black")
for i in range(z):
    x = i / 100
    xval[i] = x
    yval[i] = f(x) + gauss(0, sigma)
    move(xval[i], yval[i])
    fillCircle(0.03)

xm = mean(xval)
ym = mean(yval)
move(xm, ym)
circle(0.5)

setStatusText("E(x) = " + dec2(xm) + \
          ",  E(y) = " + dec2(ym) + \
          ",  correlation = " + dec2(correlation(xval, yval)))
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Es ergibt sich erwartungsgemäss eine hohe Korrelation, die umso grösser wird, je kleiner die Streuung sigma der Messwerte gewählt wird. Für sigma = 0 ist die Korrelation exakt 1.
Es zeigt sich auch, dass der Punkt mit den Erwartungswerten P(0.5, 0.5) auf der Geraden liegt.

 

 

REGRESSIONSGERADE, BESTER FIT

 

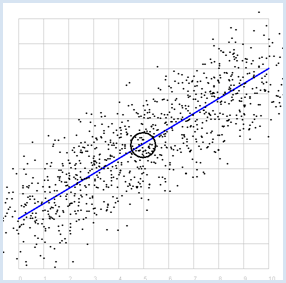
Vorher bist du von einer Geraden ausgegangen, die du "verrauscht" hast. Hier stellst du dir die umgekehrte Frage: Wie findest du die Gerade wieder heraus, wenn du nur die beiden Messreihen hast? Die gesuchte Gerade nennst du Regressionsgerade.

Immerhin weisst du schon, dass die Regressionsgerade durch den Punkt P mit den Erwartungswerten geht. Um sie zu finden, gehst du wie folgt vor:

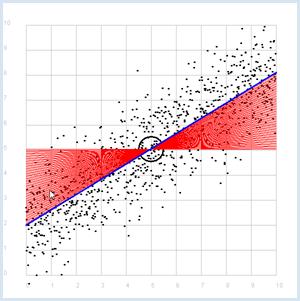
Du legst eine beliebige Gerade durch P und bestimmst für alle x die Quadrate der Abweichungen der Messwerte y von der Geraden (vertikaler Abstand). Für die Regressionsgerade müssen diese Abweichungen möglichst klein sein. Dazu bestimmst du eine Fehlersumme, indem du die einzelnen Abweichungen addierst.

Du findest in der Simulation die beste Gerade, indem du deine gelegte Gerade schrittweise um den Punkt P drehst und immer wieder die Fehlersumme bildest. Diese wird absinken. Kurz bevor die Fehlersumme wieder ansteigt, hast du den besten Fit gefunden.

 

   

from random import gauss
from gpanel import *
import math

z = 1000
a = 0.6
b = 2

def f(x):
    y = a * x + b
    return y

def dec2(x):
    return str(round(x, 2))

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

sigma = 1
    
makeGPanel(-1, 11, -1, 11)
title("Simulate data points. Press a key...")
addStatusBar(30)
drawGrid(0, 10, 0, 10, "gray")
setStatusText("Press any key")

xval = [0] * z
yval = [0] * z

for i in range(z):
    x = i / 100
    xval[i] = x 
    yval[i] = f(x) + gauss(0, sigma)
    move(xval[i], yval[i])
    fillCircle(0.03)

getKeyWait()
xm = mean(xval)
ym = mean(yval)
move(xm, ym)
lineWidth(3)
circle(0.5)

def g(x):
    y = m * (x - xm) + ym
    return y

def errorSum():
    count = 0
    for i in range(z):
        x = i / 100
        count += (yval[i] - g(x)) * (yval[i] - g(x))
    return count

m = 0
setColor("red")
lineWidth(1)
error_min = 0
while m < 5:
    line(0, g(0), 10, g(10))
    if m == 0:
        error_min = errorSum()
    else:
        if errorSum() < error_min:
            error_min = errorSum()
        else:
            break
    m += 0.01

title("Regression line found")
setColor("blue")
lineWidth(3)
line(0, g(0), 10, g(10))
setStatusText("Found slope: " +  dec2(m) + \
               ", Theory: " + dec2(covariance(xval, yval) 
              /(deviation(xval) * deviation(xval))))
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Statt den besten Fit mit einer Computersimulation zu finden, kannst du ihre Steigung auch mit

  m = (Kovarianz(x, y))/ Streuung(x)2  

berechnen. Da die Regressionsgerade durch den Punkt P mit den Erwartungswerten E(x) und E(y) geht, besitzt sie also die Geradengleichung:

y - E(y) = m * (x - E(x))

 

 

AUFGABEN

 

1.


Das bekannte Engelsche Gesetz aus der Wirtschaftswissenschaft besagt, dass in Haushalten mit steigendem Einkommen im Durchschnitt auch die Ausgaben für Nahrungsmittel zwar absolut wachsen, jedoch relativ abnehmen. Zeige mit dem Datenmaterial dessen Richtigkeit.

a. Visualisiere den Zusammenhang zwischen Einkommen und  absoluten Nahrungsmittelausgaben

b. Visualisiere den Zusammenhang zwischen Einkommen und  relativen  Nahrungsmittelausgaben

c. Bestimme die Korrelation zwischen Einkommen und absoluten Nahrungsmittelausgaben

d. Bestimmte die Regressionsgerade zwischen Einkommen und absoluten Nahrungsmittelausgaben

Daten:

Monatseinkommen
4000
4100
4200
4300
4400
4500
4600
4700
4800
4900
Ausgaben %
64
63.25
62.55
61.90
61.30
60.75
60.25
59.79
59.37
58.99

5000
5100
5200
5300
5400
5500
5600
5700
5800
5900
6000
58.65
58.35
58.08
57.84
57.63
57.45
57.30
57.17
57.06
56.97
56.90

 
2.

Die heute allgemein akzeptierte Entwicklungsgeschichte des Universums  geht davon aus, dass es vor langer Zeit einen Urknall (Big Bang) gegeben hat, und sich seitdem das Universum ausdehnt. Im Vordergrund steht die Frage, wie lange der Urknall zurückliegt, was man als Alter des Universums bezeichnet. Der Astronom Hubble hat 1929 seine weltberühmten Untersuchungen publiziert, in denen er feststellte, dass es einen linearen Zusammenhang zwischen der Distanz d der Galaxien und ihrer Fluchtgeschwindigkeit v gibt. Das Hubble-Gesetz lautet:

v = H * d

wo H die Hubble-Konstante genannt wird.

Du kannst die astrophysikalischen Überlegungen nachvollziehen, indem du von folgenden experimentellen Daten ausgehst, die vom Hubble-Weltraumteleskop stammen:

Galaxie

Distanz
 [Mpc)

Geschwindig-
keit [km/s]

NGC0300

2

133

NGC095

9.16

664

NGC1326A

16.14

1794

NGC1365

17.95

1594

NGC1425

21.88

1473

NGC2403

3.22

278

NGC2541

11.22

714

NGC2090

11.75

882

NGC3031

3.63

80

NGC3198

13.8

772

NGC3351

10

642

NGC3368

10.52

768

NGC3621

6.64

609

NGC4321

15.21

1433

NGC4414

17.7

619

NGC4496A

14.86

1424

NGC4548

16.22

1384

NGC4535

15.78

1444

NGC4536

14.93

1423

NGC4639

21.98

1403

NGC4725

12.36

1103

IC4182

4.49

318

NGC5253

3.15

232

NGC7331

14.72

999

1 Megaparsec (Mpc) = 3.09 * 1019km

a) Zeichne die Daten in einem Scatterplot auf. Kopiere sie dazu die Datenliste in dein Programm.

data = [
["NGC0300", 2.00, 133],
["NGC095", 9.16, 664],
["NGC1326A", 16.14, 1794],
["NGC1365", 17.95, 1594],
["NGC1425", 21.88, 1473],
["NGC2403", 3.22, 278],
["NGC2541", 11.22, 714],
["NGC2090", 11.75, 882],
["NGC3031", 3.63, 80],
["NGC3198", 13.80, 772],
["NGC3351", 10.0, 642],
["NGC3368", 10.52, 768],
["NGC3621", 6.64, 609],
["NGC4321", 15.21, 1433],
["NGC4414", 17.70, 619],
["NGC4496A", 14.86, 1424],
["NGC4548", 16.22, 1384],
["NGC4535", 15.78, 1444],
["NGC4536", 14.93, 1423],
["NGC4639", 21.98, 1403],
["NGC4725", 12.36, 1103],
["IC4182", 4.49, 318],
["NGC5253", 3.15, 232],
["NGC7331", 14.72, 999]]

# from Freedman et al, The Astrophysical Journal, 553 (2001)

b) Zeige, dass die Werte gut korrelieren und bestimme die Steigung H der Regressionsgeraden

c) Gehst du davon aus, dass die Geschwindigkeit v einer bestimmten Galaxie konstant geblieben ist, so ist ihre Distanz d  = v * T, wo T das Alter des Universums ist. Mit dem Hubble-Gesetz v = H * d folgt daraus T = 1 / H. Bestimme T.

 

 

 

ZUSATZSTOFF


 

MIT AUTOKORRELATION VERSTECKTE INFORMATION FINDEN

 

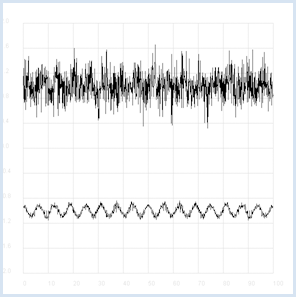
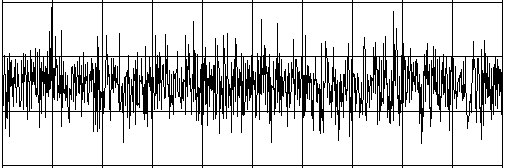
Intelligente Wesen auf einem weit entfernten Planeten möchten Kontakt mit anderen Lebewesen aufnehmen. Sie senden dazu Radiosignale aus, die eine bestimmte Regelmässigkeit aufweisen (du kannst dir darunter eine Art Morsesignale vorstellen).  Auf dem langen Übertragungsweg wird das Signal immer schwächer und immer mehr von statistisch schwankendem Rauschen überdeckt. Empfangen wir dieses Signal auf der Erde mit einem Radioteleskop, so hören wir vorerst nur das Rauschen.

Die Statistik und ein Computerprogramm kann uns aber helfen, das ursprünglich Radiosignal wieder herauszuholen. Wenn du nämlich den Korrelationskoeffizienten des Signals mit seinem eigenen zeitverschobenen Signal berechnest, so verringern sich die statistischen Rauschanteile. (Eine Korrelation mit sich selbst nennt man Autokorrelation).

Du kannst diese für die Signalanalyse bedeutsame Eigenschaft mit einem Python-Programm simulieren. Das ursprüngliche Nutzsignal ist ein Sinuston und du überlagerst ihm das Rauschen, indem du jedem Abtastwert eine Zufallszahl (mit einer Normalverteilung) addierst. Das so verrauschte Signal zeigst du im oberen Teil der Grafik und wartest auf einen Tastendruck. Das Nutzsignal ist nicht mehr erkennbar.

Nachfolgend bildest du die Autokorrelation des Signals und zeichnest den Verlauf des Korrelationskoeffizienten im unteren Teil der Grafik auf. Das Nutzsignal ist nun wieder klar erkennbar.

  


from random import gauss
from gpanel import *
import math

def mean(xval):
    n = len(xval)
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, yval):
    n = len(xval)
    xm = mean(xval)
    ym = mean(yval)
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (yval[i] - ym)
    return cxy / n

def deviation(xval):
    n = len(xval)
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

def correlation(xval, yval):
    return covariance(xval, yval)/(deviation(xval)*deviation(yval))
def shift(offset):
    signal1 = [0] * 1000
    for i in range(1000):
       signal1[i] = signal[(i + offset) % 1000]
    return signal1

makeGPanel(-10, 110, -2.4, 2.4)
title("Noisy signal. Press a key...")
drawGrid(0, 100, -2, 2.0, "lightgray")

t = 0
dt = 0.1
signal = [0] * 1000
while t < 100:
    y = 0.1 * math.sin(t) # Pure signal
#    noise = 0
    noise = gauss(0, 0.2)
    z = y + noise
    if t == 0:
        move(t, z + 1)
    else:
        draw(t, z + 1)
    signal[int(10 * t)] = z
    t += dt

getKeyWait()
title("Signal after autocorrelation")
for di in range(1, 1000):
    y = correlation(signal, shift(di))
    if di == 1:
        move(di / 10, y - 1)
    else:
        draw(di / 10, y - 1)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Noch erlebnisreicher ist es, zuerst das verrauschte Signal und dann das daraus extrahierte Nutzsignal anzuhören. Dazu verwendest du dein Wissen aus dem Kapitel Sound.

 

from soundsystem import *
import math
from random import gauss
from gpanel import *

n = 5000

def mean(xval):
    count = 0
    for i in range(n):
        count += xval[i]
    return count / n

def covariance(xval, k):
    cxy = 0
    for i in range(n):
       cxy += (xval[i] - xm) * (xval[(i + k) % n] - xm)
    return cxy / n

def deviation(xval):
    xm = mean(xval)
    sx = 0
    for i in range(n):
        sx += (xval[i] - xm) * (xval[i] - xm)
    sx = math.sqrt(sx / n)
    return sx

makeGPanel(-100, 1100, -11000, 11000)
drawGrid(0, 1000, -10000, 10000)
title("Press <SPACE> to repeat. Any other key to continue.")

signal = []
for i in range(5000):
    value = int(200 *  (math.sin(6.28 / 20 * i) + gauss(0, 4)))
    signal.append(value)
    if i == 0:
        move(i, value + 5000)
    elif i <= 1000:
        draw(i, value + 5000)

ch = 32
while ch == 32:
    openMonoPlayer(signal, 5000)
    play()
    ch = getKeyCodeWait()

title("Autocorrelation running. Please wait...")
signal1 = []
xm = mean(signal)
sigma = deviation(signal)
q = 20000 / (sigma * sigma)
for di in range(1, 5000):
    value = int(q *  covariance(signal, di))
    signal1.append(value)
title("Autocorrelation Done. Press any key to repeat.")
for i in range(1, 1000):
    if i == 1:
        move(i, signal1[i] - 5000)
    else:
        draw(i, signal1[i] - 5000)

while True:
    openMonoPlayer(signal1, 5000)
    play()
    getKeyCodeWait()

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 
 

MEMO

 

Statt das Programm auszuführen, kannst du die beiden Signale auch als WAV-Datei anhören: 

Rauschsignal (hier klicken)

Nutzsignal (hier klicken)