deutsch     english     français     Drucken

 

8.2 POPULATIONEN

 

 

EINFÜHRUNG

 

Computersimulationen werden oft dafür verwendet, um ausgehend von einer Zeitaufnahme oder einer gewissen Zeitspanne in der nahen Vergangenheit  Voraussagen über das Verhalten eines Systems in der Zukunft zu machen. Solche Prognosen können von grosser strategischer Bedeutung sein und uns beispielsweise in einem Szenario, das zu einer Katastrophe führt, zu rechtzeitigem Umdenken veranlassen. Heute  besonders aktuelle Themen sind  die Voraussage des Weltklimas und das Bevölkerungswachstum.

Unter einer Population versteht man ein System von Individuen, deren Zahl sich auf Grund von inneren Mechanismen,  Wechselwirkungen und äusseren Einflüssen in Laufe der Zeit ändert. Sieht man von äusseren Einflüssen ab, so spricht man von einem abgeschlossenen System.  Für viele Populationen ist die Veränderung der Populationsgrösse proportional zur aktuellen Grösse der Population. Aus der Zuwachsrate berechnet sich die Veränderung des aktuellen Werts mit:

   Neuer Wert - alter Wert = alter Wert * Zuwachsrate * Zeitintervall

Weil links die Differenz des neuen Werts vom alten Wert steht, nennt man diese Beziehung eine Differenzengleichung. Die Zuwachsrate kann man auch als Zunahmewahrscheinlichkeit pro Individuum und Zeiteinheit auffassen. Ist sie negativ, so nimmt die Grösse der Population ab. Die Zuwachsrate kann sich durchaus im Laufe der Zeit ändern.

PROGRAMMIERKONZEPTE:
Differenzengleichung, Zuwachsrate, Exponentielles/Begrenztes Wachstum, Sterbetafeln, Alterspyramide, Räuber-Beute-System

 

 

EXPONENTIELLES WACHSTUM

 

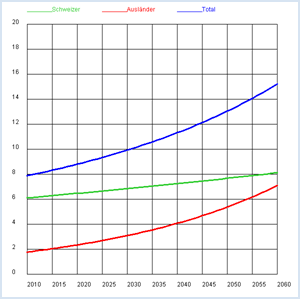
Bevölkerungsprognosen sind von grossem Interesse und können politische Entscheidungsprozesse massiv beeinflussen. Jüngstes Beispiel ist die Auseinandersetzung um die Regulierung des Ausländeranteils in der Wohnbevölkerung.

Du erhältst vom Bundesamt für Statistik (Quelle: http://www.bfs.admin.ch, Stichwort: STAT-TAB) die Einwohnerzahlen der Schweiz je für das Jahresende 2010 und 2011:

2010: Total z0 = 7 870 134, davon Schweizer s0 =  6 103 857
2011: Total z1 = 7 954 662, davon Schweizer s1 = 6 138 668

Kannst du daraus eine Prognose des Ausländeranteils für die nächsten 50 Jahre erstellen? Mit den Zahlen errechnest du zuerst die Zahl der Ausländer a0 = z0 - s0 bzw. a1 = z1 - s1 und damit die jährliche Zuwachsrate zwischen 2010 und 2011 für Schweizer und Ausländer

  rs =  (s1 - s0)/   s0 = 0.57%
bzw.
 ra =  (a1 - a0)/   a0 = 2.81%

Es ist nun für dich leicht, unter der Voraussetzung, dass diese Zuwachsraten gleich gross bleiben, die Bevölkerungszusammensetzung für die nächsten 50 Jahre zu untersuchen. Du kannst dies mit dem Taschenrechner, mit einem Tabellenkalkulationsprogramm oder mit Python machen. In einer grafischen Darstellung visualisierst du die errechneten Werte.

   


from gpanel import *

# source: Swiss Federal Statistical Office, STAT-TAB
z2010 = 7870134 # Total 2010
z2011 = 7954662 # Total 2011
s2010 = 6103857 # Swiss 2010
s2011 = 6138668 # Swiss 2011

def drawGrid():
    # Horizontal
    for i in range(11):
        y = 2000000 * i
        line(0, y, 50, y)
        text(-3, y, str(2 * i))
    # Vertical
    for k in range(11):
        x = 5 * k
        line(x, 0, x, 20000000)
        text(x, -1000000, str(int(x + 2010)))

def drawLegend():
    setColor("lime green")
    y = 21000000
    move(0, y)
    draw(5, y)
    text("Swiss")
    setColor("red")
    move(15, y)
    draw(20, y)
    text("foreigner")
    setColor("blue")
    move(30, y)
    draw(35, y)
    text("Total")
    
makeGPanel(-5, 55, -2000000, 22000000)
title("Population growth extended")
drawGrid()
drawLegend()

a2010 = z2010 - s2010 # foreigners 2010
a2011 = z2011 - s2011 # foreigners 2011

lineWidth(3)
setColor("blue")
line(0, z2010, 1, z2011)
setColor("lime green")
line(0, s2010, 1, s2011)
setColor("red")
line(0, a2010, 1, a2011)

rs = (s2011 - s2010) / s2010  # Swiss growth rate
ra = (a2011 - a2010) / a2010  # foreigners growth rate

# iteration
s = s2011
a = a2011
z = s + a
sOld = s
aOld = a
zOld = z
for i in range(0, 49):
    s = s + rs * s  # model assumptions
    a = a + ra * a  # model assumptions
    z = s + a
    setColor("blue")
    line(i + 1, zOld, i + 2, z)
    setColor("lime green")
    line(i + 1, sOld, i + 2, s)
    setColor("red")
    line(i + 1, aOld, i + 2, a)
    zOld = z
    sOld = s
    aOld = a
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Wie du aus den Zahlen entnehmen kannst, steigt der Ausländeranteil von 2010 bis 2035, also innert 25 Jahren, auf das Doppelte und in weiteren 25 Jahren auf das Vierfache. Die Populationsgrösse nimmt offenbar bei konstanter Zuwachsrate weit überproportional zu. Bezeichnest du mit T die Verdoppelungszeit, so gilt offenbar mit der Anfangsgrösse A für die Populationsgrösse y nach der Zeit t

y = A * 21/T

Da die Zeit im Exponent steht, nennt man diese rasante Zunahme ein exponentielles Wachstum.

 

 

BEGRENZTES WACHSTUM

 


Viele Populationen befinden sich in einer Umgebung  mit beschränkten Ressourcen. Dem rasanten exponentiellen Anstieg mit einer konstanten Zuwachsrate r sind daher Grenzen gesetzt. Bereits vor rund 100 Jahren hat der Biologe Carlson für eine Hefebakterien-Kultur folgende Mengen (mg) nach je einer Stunde experimentell bestimmt:

 

  


1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
9.6 18.3 29.0 47.2 71.1 119.1 174.6 257.3 350.7 441.0 513.3 559.7 594.8 629.4 640.8 651.1 655.9 659.8 661.8

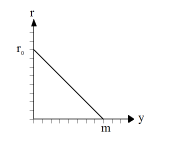
Den experimentellen Verlauf kannst du mit einem Modell verstehen, in dem das vorerst exponentielle Wachstum eine Sättigung erfährt. Dabei lässt du die Zuwachsrate mit zunehmender Populationsgrösse y linear abnehmen, bis sie bei einem bestimmten Sättigungswert m Null wird.

 

Wie du leicht durch Einsetzen von y = 0 und y = m nachprüfen kannst, gilt:

r = r0 * (1 - (y)/ m ) = (r0)/ m * ( m - y)  

Unter dieser Voraussetzung kannst du den zeitlichen Verlauf mit einem kurzen Programm grafisch darstellen, wo du auch die experimentellen Werte einzeichnest. Dazu iterierst du die Differenzengleichung, die du mit

dy: neuer Wert - alter Wert
y: alter Wert
dt: Zeitschritt
λ: Zuwachsrate

so schreiben kannst:

  dy = y * r * dt = y * r0 * (1 - (r0)/ m ) * dt  
 


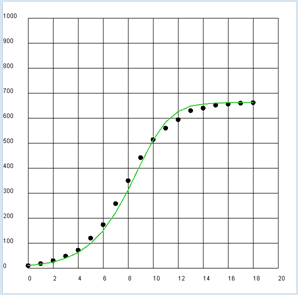
Mit dem Anfangswert y0 = 9.6 mg, der Sättigungsmenge m = 662 mg und der anfänglichen Zuwachsrate r0 = 0.62 /h ergibt sich eine gute Übereinstimmung zwischen Theorie und Experiment.

from gpanel import *

z = [9.6, 18.3, 29.0, 47.2, 71.1, 119.1, 174.6, 257.3, 350.7, 441.0, 513.3, 
559.7, 594.8, 629.4, 640.8, 651.1, 655.9, 659.6, 661.8]

def r(y):
    return r0 * (1 - y / m)

r0 = 0.62
y = 9.6
m = 662

makeGPanel(-2, 22, -100, 1100)
title("Bacterial growth")
drawGrid(0, 20, 0, 1000)
lineWidth(2)
for n in range(0, 19):
    move(n, z[n])
    setColor("black")
    fillCircle(0.2)
    if n > 0:
        dy = y * r(y)
        yNew = y + dy
        setColor("lime green")
        line(n - 1, y, n, yNew)
        y = yNew
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Geht man von einer linearen Abnahme der Zuwachsrate aus, so ergibt sich für die Populationsgrösse eine typische S-kurvenartige Sättigungskurve (auch logistisches Wachstum oder Sigmoide genannt).

 

 

STERBETAFELN

  Ein Mass für die Gesundheit einer Population ist die Wahrscheinlichkeit ein bestimmtes Altersjahr zu überleben bzw. in einem hohen Alter zu sterben. Willst du die Altersverteilung für die Schweizer Bevölkerung untersuchen, so verwendest du wieder aktuelle Daten vom Bundesamt für Statistik und zwar die sogenannten Sterbetafeln (Quelle: http://www.bfs.admin.ch, Stichwort: STAT-TAB) [mehr... Braucht nichts Makabres zu sein, denn Sterben gehört zum Leben]. 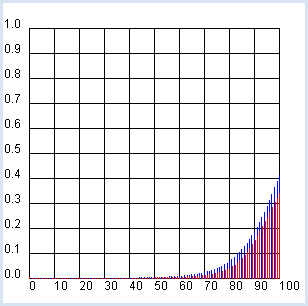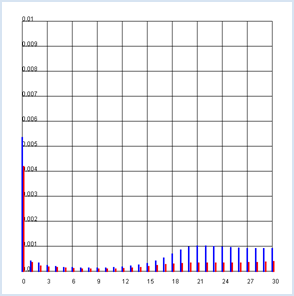Diese enthalten tabellarisch getrennt nach Männern und Frauen die beobachteten Wahrscheinlichkeiten qx und qy, in einem bestimmten Alter zu sterben. Ihre Bestimmung ist grundsätzlich einfach: Man betrachtet am Ende eines Jahres getrennt nach Männern und Frauen alle Todesfälle im vergangenen Jahr und bildet die Häufigkeit der 0-jährigen (gestorben zwischen Geburt und einem Altersjahr), der 1-jährigen, usw. Diese Zahlen teilt man nachher durch die Zahl in dieser Altersgruppe am Anfang des Jahres.


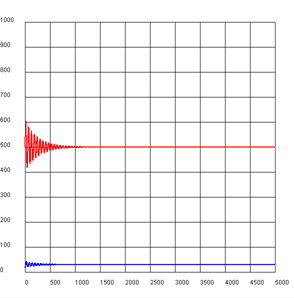
(Du kannst bei STAT-TAB eine Excel-Tabelle erstellen lassen und die Spalten für qx und qy in eine Textdatei qx.dat bzw. qy.dat kopieren oder die Dateien von hier herunterladen. Kopiere sie in das Verzeichnis, in dem sich dein Programm befindet.) Im Programm liest du die Daten in eine Liste qx bzw. qy ein. Da die Zahlen zur besseren Lesbarkeit manchmal noch Leerzeichen und Apostroph enthalten, musst du diese entfernen. Zuerst erstellst du lediglich eine grafische Darstellung der eingelesenen Daten.

 

   


import exceptions
from gpanel import *

def readData(filename):
    table = []
    fData = open(filename)

    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

makeGPanel(-10, 110, -0.1, 1.1)
title("Mortality probability (blue -> male, red  -> female)")
drawGrid(0, 100, 0, 1.0)
qx = readData("qx.dat")
qy = readData("qy.dat")
for t in range(101):
    setColor("blue")
    p = qx[t]
    line(t, 0, t, p)
    setColor("red")
    q = qy[t]
    line(t + 0.2, 0, t + 0.2, q)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 


Der Verlauf zeigt deutlich, dass Frauen im Mittel älter als Männer werden. Interessant ist auch der Verlauf in den ersten 30 Lebensjahren.

So sterben im ersten Lebensjahr deutlich mehr Knaben als Mädchen, ebenfalls in der Altersgruppe der 15 bis 30-jährigen. Mache dir darüber deine eigenen Gedanken.

  

 

 

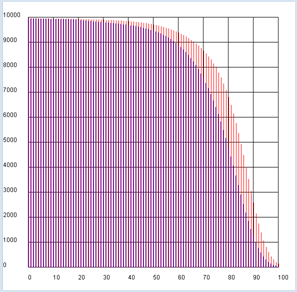
ZEITLICHE ENTWICKLUNG EINER POPULATION

 


Mit Hilfe der Sterbetafel und einem Computerprogramm kannst du viele interessante demographische Fragestellungen wissenschaftlich korrekt anpacken. Hier gehst du von 10000 Neugeborenen aus  und untersuchst, wie sich diese Population in den nächsten 100 Jahren entwickelt. Du verwendest dabei die Werte qx und qy als negative Zuwachsraten

 

   


import exceptions
from gpanel import *

n = 10000 # size of the population

def readData(filename):
    table = []
    fData = open(filename)

    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

makeGPanel(-10, 110, -1000, 11000)
title("Population behavior/predictions  (blue -> male, red -> female)")
drawGrid(0, 100, 0, 10000)
qx = readData("qx.dat")
qy = readData("qy.dat")
x = n # males
y = n # females
for t in range(101):
    setColor("blue")
    rx = qx[t]
    x = x - x * rx
    line(t, 0, t, x)
    setColor("red")
    ry = qy[t]
    y = y - y * ry
    line(t + 0.2, 0, t + 0.2, y)
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

LEBENSERWARTUNG VON FRAUEN UND MÄNNERN

 

In der vorhergehenden Untersuchung wurde nochmals deutlich, dass Frauen länger als Männer leben. Du kannst den Unterschied auch  mit einer einzigen Grösse ausdrücken, die man Lebenserwartung nennt. Es handelt sich dabei um den Mittelwert des erreichten Alters.
Rufe dir kurz in Erinnerung, wie ein Mittelwert, beispielsweise der Notendurchschnitt für eine Schulklasse, definiert ist: Du bildest die Summe s der Noten aller Schüler und dividierst sie durch die Anzahl n der Schüler. Wenn du der Einfachheit davon ausgehst, dass nur die ganzzahligen Noten von 1 bis 6 vorkommen, so könntest du s auch so berechnen:

s = Schülerzahl mit Note 1 * 1 + Schülerzahl mit Note 2 * 2 + ... Schülerzahl mit Note 6 * 6

oder allgemeiner:

Mittelwert = Summe von (Häufigkeit des Werts * Wert) dividiert durch Totalzahl

Wenn du die Häufigkeiten aus einer Häufigkeitsverteilung h der Werte x (hier der Noten 1 bis 6) entnimmst, so nennt man den Mittelwert auch Erwartungswert und du kannst dafür

  E = (x1 * h1 + x2 * h2+ ... + xn * hn)/         h1 + h2 + ... + hn

schreiben. Wie du siehst, werden in der Summe die Häufigkeiten hi mit ihrem Wert xi gewichtet.

Die Lebenserwartung ist nichts anderes als der Erwartungswert für das Alter, in dem Frauen bzw. Männer sterben. Um sie mit einer Computersimulation zu berechnen, gehst du von einer bestimmten Grösse von je n = 10000 Männern und Frauen aus und bestimmst die Zahl hx der Männer bzw. hy der Frauen, die im Alter zwischen t und t + 1 sterben. Offenbar lassen sich diese Zahlen aus der Grösse der Populationen x und y zur Zeit t, die du im vorhergehenden Programm berechnet hast, und den Sterberaten rx bzw. ry so ausdrücken:

hx = x * rx  bzw. hy = y * ry

 

n = 10000 # size of the population

def readData(filename):
    table = []
    fData = open(filename)

    while True:
        line = fData.readline().replace(" ", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

qx = readData("qx.dat")
qy = readData("qy.dat")
x = n
y = n
xSum = 0
ySum = 0
for t in range(101):
    rx = qx[t]
    x = x - x * rx
    mx = x * rx # male deaths
    xSum = xSum + mx * t # male sum
    ry = qy[t]
    y = y - y * ry
    my = y * ry # female deaths
    ySum = ySum + my * t # female sum

print "Male life expectancy:", xSum / 10000
print "Female life expectancy:", ySum / 10000
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Mit den Daten der Schweizer Bevölkerung ergeben sich für die Lebenserwartung des Mannes rund 76 Jahre und für diejenige der Frau rund 81 Jahre.

 

 

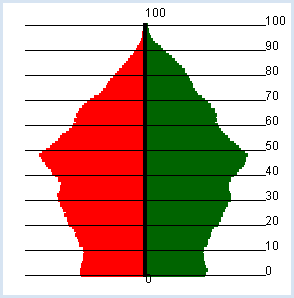
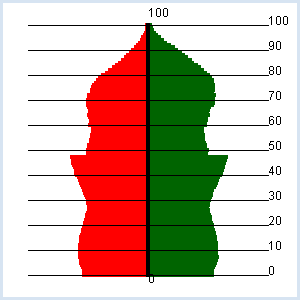
ALTERSPYRAMIDE

 

Für demografische Untersuchungen wird die Bevölkerung oft in Jahresgruppen eingeteilt und daraus ein Häufigkeitsdiagramm erstellt. Hat man zwei Gruppen, die man vergleichen möchte, so kannst du die Häufigkeiten der einen Gruppe nach links und der anderen Gruppe nach rechts auftragen. Wendest du dieses Verfahren für Männer und Frauen an, so entsteht eine hübsche pyramidenartige Grafik.

Die aktuellen Daten (31. Dezember 2012) entnimmst du wieder einer Tabelle, die du vom Bundesamt für Statistik beziehst und aus der Excel-Tabelle in die Testdateien zx.dat und zy.dat kopierst (Quelle: http://www.bfs.admin.ch, Stichwort: STAT-TAB). Du kannst sie auch von hier herunterladen.

 

   

import exceptions
from gpanel import *

def readData(filename):
    table = []
    fData = open(filename)
    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

def drawAxis():
    text(0, -3, "0")
    line(0, 0, 0, 100)
    text(0, 103, "100")

makeGPanel(-100000, 100000, -10, 110)
title("Population pyramid (green -> male, red ->  female)")
lineWidth(4)
zx = readData("zx.dat")
zy = readData("zy.dat")
for t in range(101):
    setColor("red")
    x = zx[t]
    line(0, t, -x, t)
    setColor("darkgreen")
    y = zy[t]
    line(0, t, y, t)
setColor("black")
drawAxis()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Es ist deutlich der Babyboom in den Jahren 1955 - 1965 (47 - 57 Jährige) zu erkennen.

 

 

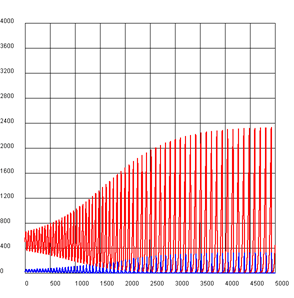
VERÄNDERUNG DER ALTERSSTRUKTUR

 

Eine Untersuchung der Veränderung der Altersstruktur über Jahrzehnte gibt wichtige Hinweise, wie sich eine Gesellschaft verändert. Du kannst die aktuelle Altersstruktur unter folgenden Voraussetzungen für die nächsten 100 Jahre simulieren:

  • Es gibt keine Zu- und Abwanderungen von Aussen (geschlossene Gesellschaft)
  • Die Todesfälle werden gemäss der Sterbetafeln berücksichtigt
  • Jede Frau im geburtsfähigen Alter von 20 bis und mit 39 bringt eine bestimmte Anzahl k Kindern zur Welt (Knaben und Mädchen gleichwahrscheinlich).  Gehe vorerst von k = 2 aus.
  

Mit einem Tastendruck kannst du immer um ein Jahr vorwärts schalten.

import exceptions
from gpanel import *

k = 2.0

def readData(filename): 
    table = []
    fData = open(filename)
    while True:
        line = fData.readline().replace(" ", "").replace("'", "")
        if line == "":
            break
        line = line[:-1] # remove trailing \n
        try:
            q = float(line)
        except exceptions.ValueError:
           break
        table.append(q)
    fData.close()
    return table

def drawAxis():
    text(0, -3, "0")
    line(0, 0, 0, 100)
    text(0, 103, "100")
    lineWidth(1)
    for y in range(11):
        line(-80000, 10* y, 80000, 10 * y)
        text(str(10 * y))

def drawPyramid():
    clear()
    title("Number of children: " + str(k) + ", year: " + str(year) + 
          ", total population: " + str(getTotal()))
    lineWidth(4)
    for t in range(101):
        setColor("red")
        x = zx[t]
        line(0, t, -x, t)
        setColor("darkgreen")
        y = zy[t]
        line(0, t, y, t)
    setColor("black")
    drawAxis()
    repaint()

def getTotal():
    total = 0
    for t in range(101):
        total += zx[t] + zy[t]
    return int(total)

def updatePop():
    global zx, zy
    zxnew = [0] * 110
    zynew = [0] * 110
    # getting older and dying
    for t in range(101):
        zxnew[t + 1] = zx[t] - zx[t] * qx[t]    
        zynew[t + 1] = zy[t] - zy[t] * qy[t]
    # making a baby
    r = k / 20
    nbMother = 0
    for t in range(20, 40):
        nbMother += zy[t]
    zxnew[0] = r / 2 * nbMother
    zynew[0] = zxnew[0]
    zx = zxnew
    zy = zynew    

makeGPanel(-100000, 100000, -10, 110)
zx = readData("zx.dat")
zy = readData("zy.dat")
qx = readData("qx.dat")
qy = readData("qy.dat")
year = 2012
enableRepaint(False)
while True:
    drawPyramid()
    getKeyWait()
    year += 1
    updatePop()
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Es zeigt sich, dass die Zukunft der Population sehr sensibel von der Zahl k abhängt. Sogar bei k = 2 nimmt sie langfristig ab.

Um bei Drücken einer Taste das Bildschirmflackern zu vermeiden, solltest du mit enableRepaint(False) das automatische Rendern abschalten. Die Grafik wird dann in drawPyramid() mit clear() nur im Hintergrundspeicher (offscreen buffer) gelöscht und erst nach der Neuberechnung mit repaint() neu auf dem Bildschirm gerendert.

 

 

AUFGABEN

 

1.


Eine Population besteht zur Zeit 0 aus 2 Individuen. Jedes Jahr nimmt sie mit der Geburtenrate 10% zu (Anzahl Geburten pro Jahr und Individuum). Simuliere sie in den ersten 100 Jahren (grafische Darstellung als Balkendiagramm).
2a.

Bei einer nicht alternden Population bleibt die Sterbewahrscheinlichkeit unabhängig vom Alter immer gleich gross. Für Lebewesen gibt es keine solchen Populationen, hingegen verhalten sich radioaktive Atome (Radionuklide) genau so. Statt von Sterbewahrscheinlichkeit spricht man hier von Zerfallswahrscheinlichkeit. Simuliere eine Population mit 10000 Radionukliden, deren Zerfallswahrscheinlichkeit 0.1 beträgt für die ersten 100 Jahre (grafische Darstellung als Balkendiagramm).

2b.

Trage im Diagramm als vertikale Linien die Zeiten ein, bei denen die Population  ungefähr auf 1/2 , auf 1/4, auf 1/8 und auf 1/16 der Anfangsgrösse geschrumpft ist. Welche Vermutung hast du?

2c*

Der radioaktive Zerfall erfolgt nach dem Gesetz

N = N0 * e -λt

No: Anzahl Radionuklide zur Zeit t = 0
N: Anzahl Radionuklide zur Zeit t
λ: Zerfallswahrscheinlichkeit pro Zeiteinheit (Zerfallskonstante)

Trage den möglichst gut angepassten Kurvenverlauf mit roter Farbe in der Grafik unter 2a ein.
3.

Die Lebenserwartung kann auch durch eine statistische Computersimulation berechnet werden. Dazu simulierst du das Leben eines einzelnen Individuums von Jahr zu Jahr. Du lässt dazu den Computer eine Zufallszahl zwischen 0 und 1 ziehen und lässt das Individuum sterben, falls diese Zahl kleiner als die Sterbewahrscheinlichkeit q ist. Die dabei erreichte Lebensdauer summierst du auf. Nachdem du die Simulation für 10000 Individuen durchgeführt hast, teilst du die erreichte Summe durch 10000. Bestimme mit diesem Verfahren mit den Werten von qy.dat die Lebenserwartung einer Frau.

 

 

 

ZUSATZSTOFF


 

RÄUBER-BEUTE-SYSTEME

 

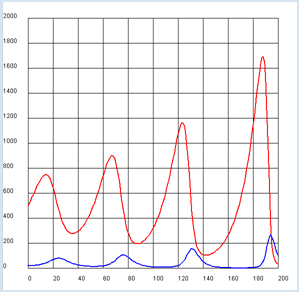
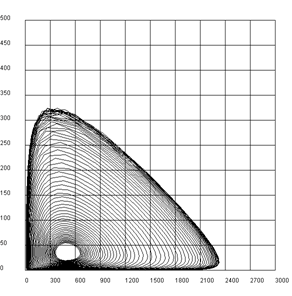
Sehr interessant ist das Verhalten von zwei Populationen, die sich in einem bestimmten Ökosystem befinden und sich gegenseitig beeinflussen. Du gehst von folgendem Szenario aus:

In einem geschlossenen Gebiet halten sich Hasen und Füchse auf. Die Hasen vermehren sich mit konstanter Zuwachsrate rx. Trifft ein Fuchs auf einen Hasen, so wird er mit der einer bestimmten Wahrscheinlichkeit vom Fuchs gerissen. Die Füchse ihrerseits sterben mit der Sterbewahrscheinlichkeit ry. Ihre Zuwachsrate ist durch den Verzerr von Hasen bestimmt.

Wenn man annimmt, dass die Wahrscheinlichkeit, dass sich Füchse und Hasen treffen gleich dem Produkt der Zahl der Hasen x  und der Füchse y ist, so ergeben sich zwei Differenzengleichungen für x und y [mehr... Bei diesen Gleichungen handelt es sich um die mathematische Formulierung der Lotka-Volterra-Regeln].

xNeu - x = rx * x - gx * x * y
yNeu - y = -ry * y + gy * x * y

Du gehst von folgenden Werten aus:

rx = 0.08
ry = 0.2
gx = 0.002
gy = 0.0004

und verwendest Anfangspopulationen von x = 500 Hasen und y = 20 Füchsen. Die Simulation führst du vorerst für 200 Generationen durch.

   


from gpanel import *

rx = 0.08
ry = 0.2
gx = 0.002
gy = 0.0004

def dx():
    return rx * x - gx * x * y

def dy():
    return -ry * y + gy * x * y
    
x = 500
y = 20

makeGPanel(-20, 220, -200, 2200)
title("Predator-Prey system (red: bunnies, blue: foxes)")
drawGrid(0, 200, 0, 2000)
lineWidth(2)
for n in range(200):
    xNew = x + dx()
    yNew = y + dy()
    setColor("red")
    line(n, x, n + 1, xNew)
    setColor("blue")
    line(n, y, n + 1, yNew)
    x = xNew
    y = yNew
Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Die Zahl der Hasen und Füchse schwankt auf und ab. Qualitativ ist dies wie folgt zu verstehen: Da sich die Füchse von den Hasen ernähren, vermehren sich die Füchse dann besonders stark, wenn es viele Hasen gibt. Da dadurch die Population der Hasen dezimiert wird, geht auch die Vermehrung der Füchse zurück. Immerhin steigt trotzdem die Zahl der Hasen (sogar über alle Grenzen).

 

 

AUFGABEN

 

1.


Führe mit sonst gleichen Werten wie oben für die Hasen eine Begrenzung des Lebensraumes gemäss dem logistischen Wachstum mit einer Zuwachsrate rx' = rx(1 - x/m) ein. Zeige, dass für m = 2000 die Schwingung mit der Zeit abklingt, hingegen für m = 3500 regelmässig wird.

 
m = 2000, Schwingung klingt ab
  

m = 3500, Schwingung wird stabil

2.

Eine Grafik, in der die Grössen der Population gegeneinander aufgetragen werden, nennt man ein Phasendiagramm. Schreibe ein Programm. dass das Phasendiagramm für die zwei Fälle von Aufgabe 1 zeichnet. Verstehst du das Verhalten?