Forum
8.5 FOLGEN, KONVERGENZ
![]()
EINFÜHRUNG |
Aneinandergereihte Zahlen faszinieren die Menschen seit langer Zeit. Bereits in der Antike um 200 v. Chr. hat Achimedes die Zahl Pi durch eine Zahlenfolge angenähert, indem er den Umfang der in den Kreis eingezeichneten regelmässigen Vielecke mit zunehmender Eckenzahl betrachtete. Bereits für ihn war offenbar klar, dass der Kreis als Grenzfall eines regelmässigen Vielecks mit immer grösser werdender Eckenzahl aufgefasst werden kann und damit auch der Umfang der Vielecke gegen den Umfang des Kreises streben musste. Eine Zahlenfolge besteht aus den Zahlen a0, a1, a2, usw., also aus den Gliedern an mit dem Index n = 0, 1, 2, usw. (Manchmal beginnt man auch mit n = 1.) Ein Bildungsgesetz bestimmt eindeutig, wie gross jede der Zahlen ist. Ist ak für alle noch so grossen natürlichen Zahlen definiert, so spricht man von einer unendlichen Zahlenfolge. Das Gesetz kann als expliziter Ausdruck von n angegeben sein. Ein Glied kann sich aber auch aus vorhergehenden Gliedern berechnen lassen (rekursives Gesetz). In diesem Fall müssen auch noch Startwerte bekannt sein. Eine konvergente Zahlenfolge hat eine sehr anschauliche Eigenschaft: Es gibt für sie eine eindeutige Zahl g, genannt Grenzwert, an die sich die Glieder immer mehr annähern, was so zu verstehen ist, dass du ein beliebig kleines Umgebungsintervall von g wählen kannst und alle Glieder von einem gewissen n nicht mehr aus diesem Intervall herausfallen. Die Umgebung kannst du dir wie ein Haus um den Grenzwert vorstellen: Die Folge kann vorerst eventuell wilde Sprünge machen, aber von einem bestimmten n an befinden sich alle Glieder im noch so kleinen Haus. 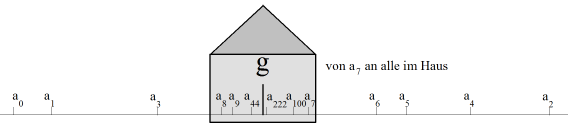 Zahlenfolgen können mit dem Computer experimentell untersucht werden. Zur Veranschaulichung verwendest du verschiedene grafische Darstellungen: Du kannst beispielsweise wie im oberen Bild auf einer Achse die Glieder als Striche oder Punkte eintragen und untersuchen, ob sich ein Häufungspunkt ergibt. Du kannst aber auch in einem x-y-Diagramm die n auf der x-Achse und an auf der y-Achse als Punkte eintragen und untersuchen, wie sich der Graf für grosse Werte von n verhält |
DER JÄGER UND SEIN HUND |
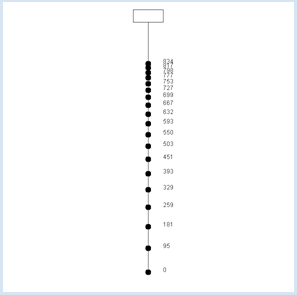
Ein Jäger spaziert mit der Geschwindigkeit u = 1 m/s mit seinem Hund zur d = 1000 m entfernten Jagdhütte. Weil der Jäger für den Hund allerdings deutlich zu langsam läuft, verfährt der Hund wie folgt: Er läuft allein mit der Geschwindigkeit u = 20 m/s bis zur Jagdhütte, kehrt dort unverzüglich um und läuft seinem Herrn entgegen. Sobald er diesen erreicht, dreht er wieder um, läuft bis zur Jagdhütte und so weiter.
woraus du mit wenig Algebra die folgende Beziehung nachweisen kannst:
Wie zu erwarten ist, häufen sich die Zahlen an gegen die Grenzzahl 1000. from gpanel import * u = 1 # m/s v = 20 # m/s d = 1000 # m a = 0 # hunter h = 0 # dog c = 2 * u / (u + v) it = 0 makeGPanel(-50, 50, -100, 1100) title("Hunter-Dog problem") line(0, 0, 0, 1000) line(-5, 1000, 5, 1000) line(-5, 1050, 5, 1050) line(-5, 1000, -5, 1050) line(5, 1000, 5, 1050) while not isDisposed(): move(0, a) fillCircle(1) text(5, a, str(int(a))) getKeyWait() da = c * (d - a) dh = 2 * (d - a) - da h += dh a += da it += 1 title("it = " + str(it) + "; hunter = " + str(a) + " m; dog = " + str(h) + " m")
|
MEMO |
|
Man sagt, dass die Folge der Zahlen an konvergiert und dass ihr Grenzwert 1000 ist. Überlege dir, warum diese Problemstellung theoretischer Natur ist. Sie entspricht aber der antiken Anekdote, wonach Achilles zum Wettlauf mit einer Schildkröte aufgefordert wurde. Da er (immerhin) zehnmal so schnell war wie die Schildkröte, sollte diese allerdings zehn Meter Vorsprung erhalten. Achilles weigerte sich anzutreten mit der Begründung, er habe keine Chance, die Schildkröte einzuholen. Er argumentierte so: In der Zeit, die er für die ersten 10 m benötige, sei die Schildkröte schon wieder 1m voraus. In der Zeit, die er für diesen Meter benötige, sei sie schon wieder 10 cm weiter. In der Zeit, die er für diese 10 cm benötige, wäre sie wieder 1cm voraus und so weiter. Was meinst du dazu? |
DAS FEIGENBAUM-DIAGRAMM |
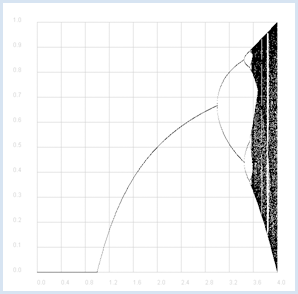
Im Zusammenhang mit der Populationsdynamik hast du das logistische Wachstum kennengelernt. Dabei wird die Populationsgrösse xnew in der nächsten Generation aus der aktuellen Grösse x aus einer quadratischen Beziehung berechnet. Im Folgenden wird der Zusammenhang vereinfacht: wo r ein frei wählbarer Parameter ist. Du stellst dir die interessante Frage, ob die daraus entstehende rekursiv definierte Folge
from gpanel import * def f(x, r): return r * x * (1 - x) makeGPanel(-0.6, 4.4, -0.1, 1.1) title("Tree Diagram") drawGrid(0, 4.0, 0, 1.0, "gray") for z in range(1001): r = 4 * z / 1000 a = 0.5 for i in range(1001): a = f(a, r) if i > 500: point(r, a)
|
MEMO |
|
Im Experiment erkennst du für ein bestimmtes r die Häufungspunkte der Folge. Du kannst auf Grund der Computersimulation folgende Vermutungen aufstellen: Für r < 1 gibt es einen Häufungspunkt bei 0, die Folge konvergiert also gehen 0. Im Bereich zwischen 1 und 3 konvergiert die Folge ebenfalls. Für noch grössere r gibt es vorerst zwei und später mehr Häufungspunkte, die Folge konvergiert also nicht mehr. Für noch grössere Werte von r springt die Folge chaotisch hin und her. |
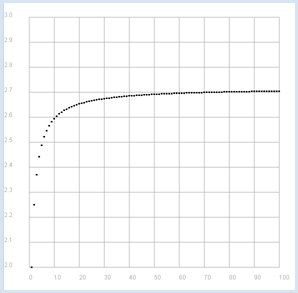
DIE EULERSCHE ZAHL |
from gpanel import * def a(n): return (1 + 1/n)**n makeGPanel(-10, 110, 1.9, 3.1) title("Euler Number") drawGrid(0, 100, 2.0, 3.0, "gray") for n in range(1, 101): move(n, a(n)) fillCircle(0.5)
|
MEMO |
Es handelt sich um die Eulersche Zahl e, die wohl berühmteste Zahl überhaupt. |
SCHNELL KONVERGIERENDE FOLGEN ZUR BERECHNUNG VON PI |
Die Berechnung von π auf möglichst viele Stellen stellt seit dem Altertum eine Herausforderung dar. Erst 1995 entdeckten die Mathematiker Bailey, Borwein und Plouffe eine Summenformel, die BBP-Formel. Sie bewiesen, dass man π exakt als Grenzwert einer Folge erhält, deren n-tes Glied die Summe von
Dein Programm verwendet das Python-Modul decimal, die Dezimalzahlen mit hoher Genauigkeit zur Verfügung stellt. Aus einem Integer oder Float erzeugt der Konstruktor eine solche Zahl, wobei die üblichen mathematischen Operationszeichen direkt verwendbar sind. Mit getcontext().prec legt man die Genauigkeit fest. Diese entspricht ungefähr der Stellenzahl der verwendeten Dezimalzahlen. Dein Programm berechnet bei jedem Tastendruck das nächste Folgeglied und stellt den Wert in einem EntryDialog dar.
from entrydialog import * from decimal import * getcontext().prec = 50 def a(k): return 1/16**Decimal(k) * (4 / (8 * Decimal(k) + 1) - 2 / (8 * Decimal(k) + 4) - 1 / (8 * Decimal(k) + 5) - 1 / (8 * Decimal(k) + 6)) inp = IntEntry("n", 0) out = StringEntry("Pi") pane0 = EntryPane(inp, out) btn = ButtonEntry("Next") pane1 = EntryPane(btn) dlg = EntryDialog(pane0, pane1) dlg.setTitle("BBP Series - Click Next") n = 0 s = a(0) out.setValue(str(s)) while not dlg.isDisposed(): if btn.isTouched(): n = inp.getValue() if n == None: out.setValue("Illegal entry") else: n += 1 s += a(n) inp.setValue(n) out.setValue(str(s))
|
MEMO |
|
Bereits mit 40 Iterationen verändert sich die angezeigte Zahl für π nicht mehr. Das Programm endet beim Schliessen des Anzeigefensters da isDisposed() True ist. |
AUFGABEN |
|
ZUSATZSTOFF |
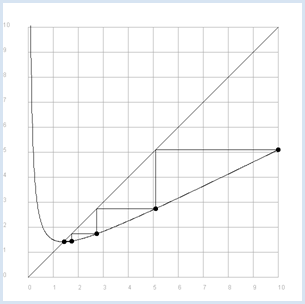
ITERATIVE LÖSUNG EINER GLEICHUNG |
from gpanel import * def f(x): return 1 / 2 * (x + 2 / x) makeGPanel(-1, 11, -1, 11) title("Iterative square root begins at x = 10. Press a key...") drawGrid(0, 10, 0, 10, "gray") for i in range(10, 1001): x = 10 / 1000 * i if i == 10: move(x, f(x)) else: draw(x, f(x)) line(0, 0, 10, 10) x = 10 move(x, f(x)) fillCircle(0.1) it = 0 while not isDisposed(): getKeyWait() it += 1 xnew = f(x) line(x, f(x), xnew, f(x)) line(xnew, f(x), xnew, f(xnew)) x = xnew move(x, f(x)) fillCircle(0.1) title("Iteration " + str(it) + ": x = " + str(x))
|
MEMO |
Du siehst deutlich, dass sich die Punkte bei jedem Tastendruck sehr schnell zum Schnittpunkt hin bewegen. Bereits mit wenigen Iterationen ergibt sich eine Lösung mit 10-stelliger Genauigkeit. |