Forum
8.8 SPEKTRALANALYSE
![]()
EINFÜHRUNG |
Fällt Licht auf dein Auge oder hörst du einen Ton, so entsteht ein Signal, das man als eine Funktion der Zeit y(t) auffassen kann. Für eine einzige Spektralfarbe oder einen reinen Ton handelt es sich um eine sinusförmige Schwingung mit der Amplitude A und Frequenz f, mathematisch ausgedrückt [mehr... Beginnt man mit der Zeitzählung nicht am Anfang der Sinusschwingung, so muss man noch eine Phasenverschiebung berücksichtigen.]:
|
SPEKTRUM EINES KLANGS, OBERTÖNE |
Für den typischen Klangcharakter einer Stimme oder eines Musikinstruments sind die sinusförmigen Frequenzanteile wichtig, die darin enthalten sind. Für einen exakt periodischen Klang bestehen diese aus dem Grundton und den Obertönen, deren Frequenz ein ganzzahliges Vielfaches der Frequenz des Grundtons ist. Trägst du die Amplituden der Frequenzanteile in einer Grafik auf, so erhältst du das Spektrum des Klangs. Ein Gerät, mit dem du das Spektrum bestimmen kannst, nennt man einen Spektralanalysator. TigerJython kann das Spektrum auf Grund eines Algorithmus bestimmen, der sehr berühmt ist und Fast Fourier Transform (FFT) heisst. Um die FFT durchzuführen, übergibst du der Funktion fft(samples, n) eine Liste samples mit den zeitlich äquidistanten Abtastwerten und der Angabe n, wieviele davon vom Anfang der Liste an für die FFT zu verwenden sind. Diese n/2 Rückgabewerte im Abstand r "bevölkern" das Frequenzgebiet von 0 bis n/2*r = fs/2, oder kurz gesagt: Bei einer Abtastrate von fs liefert die FFT das Spektrum von 0 bis fs/2. Für eine Musik-CD mit der typischen Abtastrate fs = 44100 Hz entspricht dies einem Spektrum bis 22050 Hz, das den ganzen vom Menschen hörbaren Bereich umfasst.
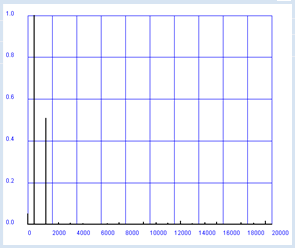
from soundsystem import * from gpanel import * def showSpectrum(text): makeGPanel(-2000, 22000, -0.2, 1.2) drawGrid(0, 20000, 0, 1.0, 10, 5, "blue") title(text) lineWidth(2) r = fs / n # Resolution f = 0 for i in range(n // 2): line(f, 0, f, a[i]) f += r fs = 40000 # Sampling frequency n = 10000 # Number of samples samples = getWavMono("wav/doublesine.wav") openMonoPlayer(samples, fs) play() a = fft(samples, n) showSpectrum("Audio Spectrum") |
MEMO |
Wie du vermutest (und hörst), handelt es sich um die Frequenzen 500 Hz und 1.5 kHz mit einem Amplitudenverhältnis von 1 : 1/2. Zusätzlich gibt es noch einige Störungsanteile. Die Frequenz 0 entspricht einem konstanten Signalanteil (offset). Du hast jetzt mit TigerJython einen feudalen Spektrumanalysator vor dir, mit dem du die Grund- und Obertöne von Musikinstrumenten und menschlichen oder tierischen Lauten untersuchen kannst. In der Distribution findest du bereits den Ton einer Flöte ("wav/flute.wav") und einer Oboe ("wav/oboe.wav"), deren Klangcharakteristik sehr unterschiedlich sind. |
|
SPEKTRUM FÜR SELBSTDEFINIERTE FUNKTIONEN |
Gemäss dem Satz von Fourier ist jede periodische Funktion mit der Frequenz f als Überlagerung von Sinusfunktionen mit den Frequenzen f, 2*f, 3*f, usw. darstellbar (Fourierreihe).
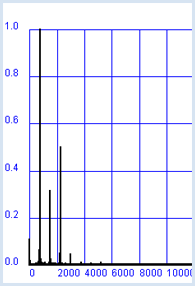
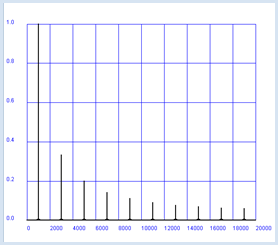
from soundsystem import * from gpanel import * def showSpectrum(text): makeGPanel(-2000, 22000, -0.2, 1.2) drawGrid(0, 20000, 0, 1.0, 10, 5, "blue") title(text) lineWidth(2) r = fs / n # Resolution f = 0 for i in range(n // 2): line(f, 0, f, a[i]) f += r n = 10000 fs = 40000 # Sampling frequency f = 1000 # Signal frequency samples = [0] * 120000 # sampled data for 3 s t = 0 dt = 1 / fs # sampling period for i in range(120000): samples[i] = square(1000, f, t) t += dt openMonoPlayer(samples, 40000) play() a = fft(samples, n) showSpectrum("Spectrum Square Wave") |
MEMO |
Das Experiment betätigt die Theorie, wonach das Spektrum einer Rechteckfunktion aus den ungeraden Vielfachen der Grundfrequenz besteht und sich die Amplituden der Spektralanteile wie 1, 1/3, 1/5, 1/7, usw. verhalten. Du kannst aber nie experimentell herausfinden, dass die spektralen Anteile theoretisch bis ins Unendliche reichen. |
SONOGRAMME |
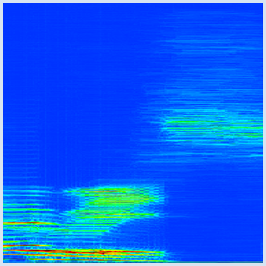
Die FFT ist ein perfektes Tool, um den spektralen Verlauf eines sich zeitlich ändernden Lauts aufzuzeichnen, beispielsweise eines gesprochenen Worts. Das Signal ist in diesem Fall natürlich nicht mehr periodisch, man kann aber davon ausgehen, dass es wenigstens stückweise einigermassen periodisch ist. Darum wendet man die FFT für kurze Signalblöcke an, beispielsweise für eine Blocklänge von 100 ms und wiederholt dies alle 2.5 ms. Damit ergibt sich alle 2.5 ms ein neues Spektrum, das man in einem Sonogramm als kolorierte vertikale Linie darstellen kann.
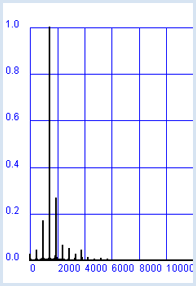
from soundsystem import * from gpanel import * def toColor(z): w = int(450 + 300 * z) c = X11Color.wavelengthToColor(w) return c def drawSonogram(): makeGPanel(0, 190, 0, 1000) title("Sonogramm of 'Harris'") lineWidth(4) # Analyse blocks every 50 samples for k in range(191): a = fft(samples[k * 50:], n) for i in range(n // 2): setColor(toColor(a[i])) point(k, i) fs = 20000 # Sampling freq->spectrum 0..10 kHz n = 2000 # Size of block for analyser samples = getWavMono("wav/harris.wav") openMonoPlayer(samples, fs) play() drawSonogram() |
MEMO |
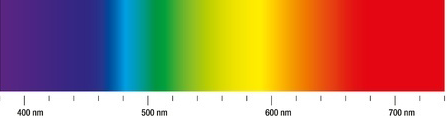
Das Sonogramm zeigt vertikal Frequenzen im Bereich 0..10 kHz, horizontal den zeitlichen Verlauf von 0 bis 190 * 50 / 20000 = 0.475 s. Für die Umsetzung von Zahlen in Farben ist es zweckmässig, die Funktion X11Color.wavelengthToColor() zu verwenden, die Wellenlängen des Farbspektrums im Bereich 380...780 nm in Farben umsetzt. Deutlich sichtbar sind die hohen Spektralanteile beim Zischlaut "s", bei dem die Grundtöne gänzlich fehlen. |
LICHTSPEKTREN |
Auch Licht kann spektral zerlegt werden, um die darin enthaltenen Wellenlängenanteile zu bestimmen. Das sichtbare Spektrum liegt im Wellenlängenbereich von ungefähr 380 nm bis 780 nm
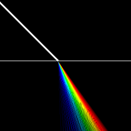
Als Spektrumanalysator für Licht kennst du sicher das Prisma, bei dem das Licht für verschiedenen Wellenlängen gemäss dem Brechungsgesetz verschieden stark abgelenkt (gebrochen) wird.
In deinem Programm simulierst du den Übergang eines weissen Lichtstrahls in Glas und zeigst in einer Vergrösserung den Lichtweg für verschiedene Farben. from gpanel import * # K5 glass B = 1.5220 C = 4590 # nanometer^2 # Cauchy equation for refracting index def n(wavelength): return B + C / (wavelength * wavelength) makeGPanel(-1, 1, -1, 1) title("Refracting at the K5 glass") bgColor("black") setColor("white") line(-1, 0, 1, 0) lineWidth(4) line(-1, 1, 0, 0) lineWidth(1) sineAlpha = 0.707 for i in range(51): wavelength = 380 + 8 * i setColor(X11Color.wavelengthToColor(wavelength)) sineBeta = sineAlpha / n(wavelength) x = (sineBeta - 0.45) * 100 - 0.5 # magnification line(0, 0, x, -1) |
MEMO |
Um eine schöne Grafik zu erhalten, spaltest du die Farben mehr auf, als dies in Wirklichkeit der Fall ist. |
AUFGABEN |
|