Forum
8.4 MITTLERE WARTEZEITEN
![]()
EINFÜHRUNG |
|
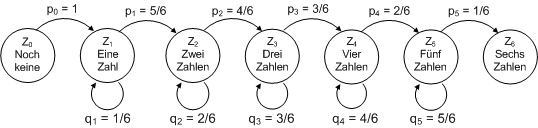
Es gibt viele Systeme, deren zeitliches Verhalten du als Übergang von einem Systemzustand zu einem nächsten beschreiben kannst. Dabei ist der Übergang vom aktuellen Systemzustand Zi zum Nachfolgezustand Zk durch Wahrscheinlichkeiten pikbestimmt. Im Folgenden würfelst du mit einem Würfel und betrachtest die bereits geworfenen Augenzahlen als Zustandsgrösse: Z0 : noch keine Augenzahl geworfen Du kannst den Übergang der Zustände im folgenden Schema veranschaulichen (sogenannte Markoff-Kette):
Die Wahrscheinlichkeiten erklären sich wie folgt: Hast du bereits n Augenzahlen geworfen, so ist die Wahscheinlichkeit, wieder eine dieser Zahlen zu erhalten n/6 und die Wahrscheinlichkeit, eine noch nicht nicht vorhandene zu erhalten (6 - n)/6. Du stellst dir die interessante Frage, wie oft du im Mittel den Würfel werfen musst, um alle sechs Zahlen zu erwürfeln.
|
MITTLERE WARTEZEITEN |
Wenn du in gleichen Zeitschritten würfelst, so kannst du dich auch fragen, wie lange im Mittel der Prozess dauert. Diese Zeit nennst du die mittlere Wartezeit. Du erhältst sie aus folgender Überlegung: Die totale Zeit, um von Z0 zu Z6 zu gelangen, ist die Summe der Wartezeiten für alle Übergänge. Wie gross sind aber die einzelnen Wartezeiten? In deinem ersten Programm findest du experimentell die wichtigste Eigenschaft von Wartezeitproblemen heraus.: Ist p die Wahrscheinlichkeit um von Z1 nach Z2 zu gelangen, so beträgt die Wartezeit (in einer geeigneten Einheit) u = 1/p.
from gpanel import * from random import randint n = 10000 p = 1/6 def sim(): k = 1 r = randint(1, 6) while r != 6: r = randint(1, 6) k += 1 return k makeGPanel(-5, 55, -200, 2200) drawGrid(0, 50, 0, 2000) title("Waiting on a 6") h = [0] * 51 lineWidth(5) count = 0 repeat n: k = sim() count += k if k <= 50: h[k] += 1 line(k, 0, k, h[k]) mean_exp = count / n lineWidth(1) setColor("red") count = 0 for k in range(1, 1000): pk = (1 - p)**(k - 1) * p nk = n * pk count += nk * k if k <=50: line(k, 0, k, nk) mean_theory = count / n title("Experiment: " + str(mean_exp) + "Theory: " + str(mean_theory)) |
MEMO |
|
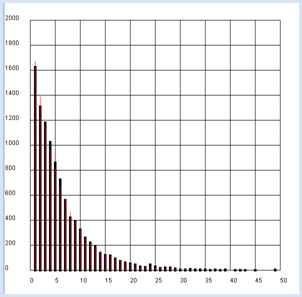
Das Resultat ist intuitiv einleuchtend: Da die Wahrscheinlichkeit, eine bestimmte Augenzahl zu würfeln p= 1/6 ist, benötigst du im Mittel u = 1 / p = 6 Würfe um diese Augenzahl zu erhalten. Es ist auch instruktiv, die theoretischen Werte der Häufigkeiten als rote Linie einzutragen. Dazu überlegst du dir, dass für die Wahrscheinlichkeiten eine 6 zu werfen, gilt:
Für die theoretischen Häufigkeiten multiplizierst du diese Wahrscheinlichkeiten mit der Anzahl n der Versuche [mehr...
Mit ein wenig Algebra kann man beweisen, dass der Erwartungswert der |
PROGRAMMIEREN STATT VIEL RECHNEN |
Um nun die oben formulierte Aufgabe zu lösen, die mittlere Wartezeit zu berechnen, bis du alle Augenzahlen mindestens einmal geworfen hast, kannst du einerseits den theoretischen Weg einschlagen. Du fasst den Prozess als Markoff-Kette auf und addierst die Wartezeiten für die einzelnen Übergänge: u = 1 + 6/5 + 6/4 + 6/3 + 6/2 + 6 = 14.7 Andererseits kannst du ein einfaches Programm schreiben, um diese Zahl in einer Simulation zu bestimmen. Dazu gehst du immer gleich vor: Du schreibst eine Funktion sim(), in welcher der Computer mit Zufallszahlen eine einzelne Lösung sucht und gibst die benötigte Anzahl Schritte als Returnwert zurückgibt. Dann wiederholst du diese Tätigkeit sehr oft, sagen wir einige tausend Mal, und bestimmst den Mittelwert. Es ist elegant, in sim() eine Liste z zu verwenden, in die du die geworfenen Zahlen einfügst, falls sie sich nicht bereits darin befinden. Wenn die Liste 6 Elemente hat, hast du alle Augenzahlen geworfen. from random import randint n = 10000 def sim(): z = [] i = 0 while True: r = randint(1, 6) i += 1 if not r in z: z.append(r) if len(z) == 6: return i count = 0 repeat n: count += sim() print("Mean waiting time:", count / n) |
MEMO |
Du erhältst in der Computersimulation den leicht schwankenden Wert von 14.68, was der theoretischen Voraussage entspricht. Der Computer kann also auch dazu dienen, schnell zu überprüfen, ob ein theoretisch errechneter Wert überhaupt stimmen kann.
Die theoretische Bestimmung von Wartezeiten kann aber bereits bei einfachen Problemen sehr aufwendig sein. Fragst du etwa nach der mittleren Wartezeit, bis du durch aufeinanderfolgendes Würfeln eine bestimmte Augensumme erreichst, so ist das Problem mit einer Computersimulation extrem einfach zu lösen. from random import randint n = 10000 s = 7 # rolled count of the die numbers def sim(): i = 0 total = 0 while True: i += 1 r = randint(1, 6) total += r if total >= s: break return i count = 0 repeat n: count += sim() print("Mean waiting time:", count / n) |
MEMO |
Du erhältst für die Augensumme 7 eine mittlere Wartezeit von etwa 2.52. Dieses Resultat ist insofern erstaunlich, als dass der Erwartungswert für die Augenzahlen ja 3.5 ist und man deswegen annehmen könnte, dass man für die Augensumme 7 im Mittel 2x würfeln muss. Die theoretische Berechnung, für die du mit einem Zeitaufwand von mehreren Stunden rechnen musst, ergibt 117 577 / 46 656 = 2.5008. Sogar Mathematiker verwenden darum den Computer, um theoretische Resultate einem schnellen Test zu unterziehen und Vermutungen zu überprüfen. |
AUSBREITUNG EINER KRANKHEIT |
Du gehst von der folgenden Geschichte aus, die zwar erfunden ist, aber durchaus gewisse Parallelen zu aktuellen Lebensgemeinschaften hat.
Es ist elegant, die Population durch eine Liste mit booleschen Werten zu modellieren, wobei gesund mit False und krank mit True codiert sind. Der Vorteil dieser Datenstruktur besteht darin, dass sich die Wechselwirkung beim Zusammentreffen von zwei Personen in der Funktion pair() mit einer logischen OR-Verknüpfung ausdrücken lässt:
from gpanel import * from random import randint def pair(): # Select two distinct inhabitants a = randint(0, 99) b = a while b == a: b = randint(0, 99) z[a] = z[a] or z[b] z[b] = z[a] def nbInfected(): count = 0 for i in range(100): if z[i]: count += 1 return count makeGPanel(-50, 550, -10, 110) title("The spread of an illness") drawGrid(0, 500, 0, 100) lineWidth(2) setColor("blue") z = [False] * 100 tmax = 500 t = 0 a = randint(0, 99) z[a] = True # random infected inhabitant move(t, 1) while t <= tmax: pair() infects = nbInfected() t += 1 draw(t, infects) |
MEMO |
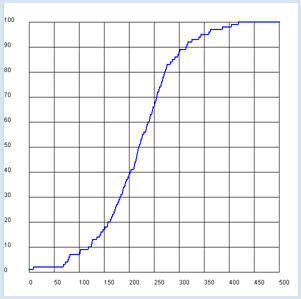
Du findest ein zeitliches Verhalten, bei dem die Zunahme zuerst langsam, dann rasant und dann wieder langsam ist. Qualitativ ist dir dieses Verhalten sicher plausibel, denn zuerst ist die Wahrscheinlichkeit gering, dass sich ein Kranker mit einem Gesunden trifft, da sich vor allem Gesunde untereinander treffen. Am Schluss ist die Wahrscheinlichkeit wiederum gering, dass ein übrig gebliebener Gesunder einem Kranken begegnet, da sich vor allem Kranke untereinander treffen [mehr... Der Verlauf entspricht tendenziell dem logistischen Wachstum]. |
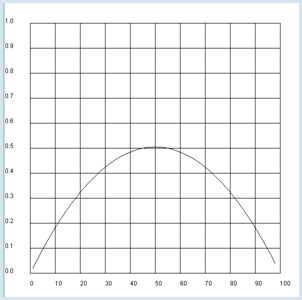
from random import randint n = 1000 # number experiment def pair(): # Select two distinct inhabitants a = randint(0, 99) b = a while b == a: b = randint(0, 99) z[a] = z[a] or z[b] z[b] = z[a] def nbInfected(): count = 0 for i in range(100): if z[i]: count += 1 return count def sim(): global z z = [False] * 100 t = 0 a = randint(0, 99) z[a] = True # random infected inhabitant while True: pair() t += 1 if nbInfected() == 100: return t count = 0 for i in range(n): u = sim() print("Experiment #", i + 1, "Waiting time:", u) count += u print( "Mean waiting time:", count / n) Du kannst die Ausbreitung der Krankheit aber auch als Markoff-Kette auffassen. Ein bestimmter Zustand ist durch die Zahl der Infizierten charakterisiert. Für eine Population mit 100 Personen ist die Wartezeit, bis alle krank sind, die Summe der Wartezeiten für die Übergänge von k Kranken zu k+1 Kranken für k von 1 bis 99. Dazu benötigst du die Wahrscheinlichkeit pk für diesen Übergang. Es gilt:
from gpanel import * n = 100 def p(k): return 2 * k * (n - k) / n / (n - 1) makeGPanel(-10, 110, -0.1, 1.1) drawGrid(0, 100, 0, 1.0) count = 0 for k in range(1, n - 1): if k == 1: move(k, p(k)) else: draw(k, p(k)) count += 1 / p(k) title("Time until everyone is ill: " + str(count)) |
MEMO |
Mit der Theorie der Markoff-Ketten ergibt sich eine mittlere Wartezeit von 463 Stunden, also rund 20 Tage. |
PROGRAMM FÜR PARTNERSUCHE |
Für die Praxis interessant ist die Frage nach einer optimalen Strategie bei der Wahl eines Lebenspartners. Dabei gehst du von folgender Modellannahme aus: 100 mögliche Partner besitzen aufsteigende Qualifikationswerte. Sie werden dir in zufällig durchmischter Reihenfolge vorgestellt und du kannst sie in dieser "Lernphase" durch deine bisher erreichte Lebenserfahrung in der Reihenfolge ihrer Qualifikationswerte richtig einordnen. Du weist allerdings nicht, welches der maximale Qualifikationsgrad ist. Bei jeder Vorstellung musst du dich für den Partner entscheiden oder du weist ihn zurück. Wie musst du vorgehen, damit du mit hoher Wahrscheinlichkeit den Partner mit der besten Qualifikation wählst? Für die Simulation erstellst du in der Funktion sim(x) eine Liste t mit den 100 Qualifikationswerten 0..99 in beliebiger Reihenfolge. Es handelt sich um eine Zufallspermutation der Zahlen 0..99, die du in Python elegant mit shuffle() erzeugen kannst.
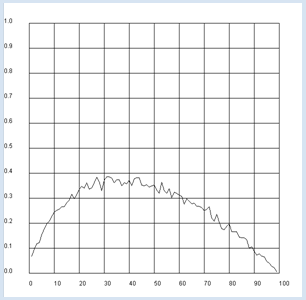
from random import shuffle from gpanel import * n = 1000 # Number of simulations a = 100 # Number of partners def sim(x): # Random permutation [0..99] t = [0] * 100 for i in range(0, 100): t[i] = i shuffle(t) best = max(t[0:x]) for i in range(x, 100): if t[i] > best: return [i, t[i]] return [99, t[99]] makeGPanel(-10, 110, -0.1, 1.1) title("The probability of finding the best partner from 100") drawGrid(0, 100, 0, 1.0) for x in range(1, 100): count = 0 repeat n: z = sim(x) if z[1] == 99: # best score count += 1 p = count / n if x == 1: move(x, p) else: draw(x, p)
|
MEMO |
Es zeigt sich, dass du bei einer Länge der Lernphase von etwas 37 die grösste Wahrscheinlichkeit hast, den Partner mit der besten Qualifikation zu finden [mehr... Der theoretische Wert beträgt 100 / e]. |
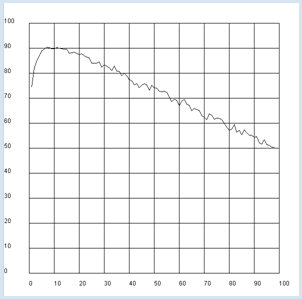
from random import shuffle from gpanel import * n = 1000 # Number of simulations def sim(x): # Random permutation [0..99] t = [0] * 100 for i in range(0, 100): t[i] = i shuffle(t) best = max(t[0:x]) for i in range(x, 100): if t[i] > best: return [i, t[i]] return [99, t[99]] makeGPanel(-10, 110, -10, 110) title("Mean qualification after waiting for a partner") drawGrid(0, 100, 0, 100) for x in range(1, 99): count = 0 repeat n: u = sim(x) count += u[1] y = count / n if x == 1: move(x, y) else: draw(x, y) |
MEMO |
Es zeigt sich ein völlig anders Bild: Du solltest dich nach dem Kriterium einer möglichst grossen mittleren Qualifikation bereits nach einer Lernphase von ungefähr 10 für den nächst besser bewerteten Partner entscheiden. Du kannst die Simulation auf für eine realistischere Zahl von Partnern durchführen und bemerkst, dass die optimale Lernphase kurz ist. |
WARTEZEITPARADOXON |
Da sie auch dann noch im Mittel alle 6 Minuten vorbei kommen, nimmst du vielleicht an, dass sich an der mittleren Wartezeit von 3 Minuten nichts ändert. Die erstaunliche, und darum paradoxe Antwort ist, dass die mittlere Wartezeit nun grösser als 3 Minuten wird. In einer animierten Simulation sollst du herausfinden, wie gross die Wartezeit unter der Annahme ist, dass die Busse gleichverteilt im Bereich 2 und 10 Minuten (in der Simulation sind es Sekunden) hintereinander fahren. Dabei verwendest du mit Vorteil die Game-Library JGameGrid ein, da sich die beteiligten Objekte, wie Busse und Fahrgäste als Sprite-Objekte modellieren lassen.
Der Programmcode erfordert einige Erklärungen: Da es sich beim Bus und den Fahrgästen offensichtlich um Objekte handelt, werden diese in den Klassen Bus bzw. Passenger modelliert. Du Busse werden am Ende des Hauptteil des Programms in einer Endlosschleife gemäss der statistischen Vorgaben erzeugt Schliesst man das Grafikfenster, so bricht die Endlosschleife wegen isDisposed() = False ab und das Programm endet. Die Fahrgäste müssen periodisch erzeugt und in der Wartereihe angezeigt werden. Dazu schreibst du am besten eine Klasse PassengerFactory die von Actor abgeleitet wird. Diese besitzt zwar keine Spritebild, ihr act() kann aber dazu verwendet werden, die Fahrgäste zu erzeugen und ins GameGrid einzufügen. Mit dem Zykluszähler nbCycles kannst du die Periode wählen, mit der die Objekte erzeugt werden (der Simulationszyklus ist auf 50 ms eingestellt). Im act() der Klasse Bus bewegst du den Bus vorwärts und prüfst mit der x-Koordinate, ob er bei der Haltestelle angekommen ist. Du rufst in diesem Moment die Methode board() der Klasse PassengerFactory auf, wodurch die wartenden Fahrgäste aus der Wartereihe entfernt werden. Gleichzeitig änderst du mit show(1) das Spritebild des Busses und zeigst die neue Wartezeit zum nachfolgenden Bus auf der Anzeigetafel an. Damit diese Aktionen nur einmal aufgerufen werden, verwendest du die boolesche Variable isBoarded. Die Anzeigetafel als Instanz der Klasse InformationPanel ist ein zusätzliches Gadget, um den Fahrgästen und Zuschauern des Programms die Distanz zum nächst folgenden Bus anzuzeigen. Die Anzeige wird wieder in der Methode act() verändert, indem mit show() eines der 10 Spritebilder digit_0.png bis digit_9.png ausgewählt wird. from gamegrid import * from random import random, randint import time min_value = 2 max_value = 10 def random_t(): return min_value + (max_value - min_value) * random() # ---------------- class PassengerFactory ---------- class PassengerFactory(Actor): def __init__(self): self.nbPassenger = 0 def board(self): for passenger in getActors(Passenger): passenger.removeSelf() passenger.board() self.nbPassenger = 0 def act(self): if self.nbCycles % 10 == 0: passenger = Passenger( randint(0, 1)) addActor(passenger, Location(400, 120 + 27 * self.nbPassenger)) self.nbPassenger += 1 # ---------------- class Passenger ----------------- class Passenger(Actor): totalTime = 0 totalNumber = 0 def __init__(self, i): Actor.__init__(self, "sprites/pupil_" + str(i) + ".png") self.createTime = time.clock() def board(self): self.waitTime = time.clock() - self.createTime Passenger.totalTime += self.waitTime Passenger.totalNumber += 1 mean = Passenger.totalTime / Passenger.totalNumber setStatusText("Mean waiting time: " + str(round(mean, 2)) + " s") # ---------------- class Car ----------------------- class Bus(Actor): def __init__(self, lag): Actor.__init__(self, "sprites/car1.gif") self.lag = lag self.isBoarded = False def act(self): self.move() if self.getX() > 320 and not self.isBoarded: passengerFactory.board() self.isBoarded = True infoPanel.setWaitingTime(self.lag) if self.getX() > 1650: self.removeSelf() # ---------------- class InformationPanel ---------- class InformationPanel(Actor): def __init__(self, waitingTime): Actor.__init__(self, "sprites/digit.png", 10) self.waitingTime = waitingTime def setWaitingTime(self, waitingTime): self.waitingTime = waitingTime def act(self): self.show(int(self.waitingTime + 0.5)) if self.waitingTime > 0: self.waitingTime -= 0.1 periodic = askYesNo("Departures every 6 s?") makeGameGrid(800, 600, 1, None, None, False) addStatusBar(20) setStatusText("Acquiring data...") setBgColor(Color.white) setSimulationPeriod(50) show() doRun() if periodic: setTitle("Warting Time Paradoxon - Departure every 6 s") else: setTitle("Waiting Time Paradoxon - Departure between 2 s and 10 s") passengerFactory = PassengerFactory() addActor(passengerFactory, Location(0, 0)) addActor(Actor("sprites/panel.png"), Location(500, 120)) addActor(TextActor("Next Bus"), Location(460, 110)) addActor(TextActor("s"), Location(540, 110)) infoPanel = InformationPanel(4) infoPanel.setSlowDown(2) addActor(infoPanel, Location(525, 110)) while not isDisposed(): if periodic: lag = 6 else: lag = random_t() bus = Bus(lag) addActor(bus, Location(-100, 40)) a = time.clock() while time.clock() - a < lag and not isDisposed(): delay(10)
|
MEMO |
Die Simulation zeigt, dass die mittlere Wartezeit mit rund 3.5 Minuten deutlich länger als die vermuteten 3 Minuten ist. Du kannst dir diese Verlängerung wie folgt erklären: Kommen die Busse gleichverteilt einmal mit 2 Minuten und mit 10 Minuten Abstand, so ist es viel wahrscheinlicher, dass deine Ankunft in das Warteintervall von 2 bis 10 Minuten fällt als in das Warteintervall von 0 bis 2 Minuten. Daher wartest du sicher länger als 3 Minuten. |
AUFGABEN |
|