deutsch     english     français     Drucken

 

11.1 VERGNÜGLICHE DENKSPIELE

 

 

EINFÜHRUNG

 

Denkspiele mit mathematischem Hintergrund sind sehr beliebt und weit verbreitet. Es geht in diesem Kapitel nicht darum, dir die Freude am eigenständigen Lösen solcher Rätsel "von Hand", also mit Papier und Schreibstift zu verderben. Vielmehr sollst du erleben, dass der Computer durch systematisches Lösen mit Backtracking die Lösung zwar auch finden kann, allerdings mit zwei wichtigen Unterschieden: Falls im Lösungsprozess nicht weitere Einschränkungen und Strategien eingebaut werden, kann zur Lösung trotz eines schnellen Computers enorm viel Zeit benötigt werden, im Gegenzug kann aber der Computer im Prinzip alle Lösungen finden, was von Hand meist sehr schwierig ist. Dadurch ist es möglich, mit dem Computer den Beweis zu liefern, dass eine bestimmte Lösung die einfachste (kürzeste) ist.

 

 

SUDOKU

 

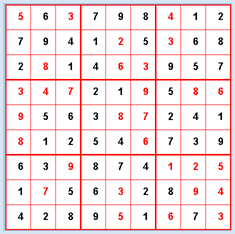
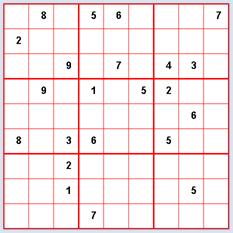
Das Spiel hat sich seit 1980 boomartig verbreitet und ist heute sehr populär. Du findest Spielvorgaben in der Rätselecke von vielen Tages- und Wochenzeitungen. Es handelt sich um ein typisches Zahlenrätsel mit einfachen Spielregeln. In der Standardvariante müssen in einem 9x9 Gitter die Zahlen 1 bis 9  derart in die Felder gesetzt werden, dass in jeder Zeile und jeder Spalte alle Zahlen genau einmal vorkommen. Zudem wird das Gitter in 9 Untergitter mit 3x3 Feldern aufgeteilt, wobei auch in diesen die Zahlen genau einmal auftreten müssen. Zu Beginn des Spiels ist bereits eine bestimmte Anzahl der Zellen besetzt. Bei idealer Spielvorgabe sollte es genau eine Lösung geben.

Je nach Spielvorgabe ist das Rätsel leichter oder schwieriger zu lösen. Der geübte Sudoku-Spieler geht mit gewissen allgemein bekannten oder auch persönlichen Lösungsstrategien vor. Beim Backtracking mit dem Computer werden systematisch die offenen Felder der Reihe nach mit Zahlen von 1 bis 9 so gefüllt, dass sich kein Widerspruch zu den Spielregeln ergibt. Ist dies nicht möglich, so wird der letzte Zug zurückgenommen.

Der Computer verwendet im Folgenden den Backtracking-Algorithmus. Für die grafische Darstellung eignet sich ein GameGrid hervorragend, da das Spiel eine Gitterstruktur aufweist. Die Vorgabezahlen zeichnest du als TextActor schwarz ein, die eingesetzten Zahlen sind rot.

Wie du aus dem Kapitel 10.3. über Backtracking weisst, musst du zuerst eine günstige Datenstruktur für die Spielzustände finden. Da es sich hier um ein 9x9-Gitter handelt, wählst du eine Liste mit den 9 Zeilenlisten. Die Zahl 0 kennzeichnet ein leeres Feld. Das hier gezeigte Spiel hat also zu Spielbeginn folgenden Zustand:

  

startState = [ \
[0, 6, 0, 7, 9, 8, 0, 1, 2],
[7, 9, 4, 1, 0, 5, 0, 6, 8],
[2, 0, 1, 4, 0, 0, 9, 5, 7],
[0, 0, 0, 2, 1, 0, 5, 0, 0],
[0, 5, 6, 3, 0, 0, 2, 4, 1],
[0, 1, 2, 5, 4, 0, 7, 3, 9],
[6, 3, 0, 8, 7, 4, 0, 0, 0],
[1, 0, 5, 6, 0, 2, 8, 0, 0],
[4, 2, 8, 9, 0, 1, 0, 7, 0]]

Wie gewohnt wirst du das Programm schrittweise entwickeln. Deine erste Aufgabe besteht darin, den Spielzustand im GameGrid darzustellen und dem Benutzer die Möglichkeit zu geben, mit einem Mausklicks die leeren Zellen zu belegen. Dies ist zwar für die automatische Lösungssuche überflüssig, erlaubt dir aber, interaktiv auf das Spiel einzuwirken, was besonders in der Testphase hilfreich ist. Zudem kannst du so das Rätsel am Bildschirm statt auf Papier lösen.

from gamegrid import *

def pressEvent(e):
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in fixedLocations:
        setStatusText("Location fixed")
        return
    x = loc.x
    y = loc.y
    value = startState[y][x]
    value = (value + 1)  % 10
    startState[y][x] = value
    showState(startState)
    
def showState(state):
    removeAllActors()
    for y in range(9):
        for x in range(9):
            loc = Location(x, y)
            value = state[y][x]
            if  value != 0:
                if loc in fixedLocations:
                    c = Color.black
                else:
                    c = Color.red
                digit = TextActor(str(value), c, Color.white, 
                        Font("Arial", Font.BOLD, 20))
                addActorNoRefresh(digit, loc)
    refresh()
    
makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent)
show()
setTitle("Sudoku")
setBgColor(Color.white)
getBg().setLineWidth(3)
getBg().setPaintColor(Color.red)
for x in range(4):
    getBg().drawLine(150 * x, 0, 150 * x, 450) 
for y in range(4):
    getBg().drawLine(0, 150 * y, 450, 150 * y) 

startState = [ 
[0, 6, 0, 7, 9, 8, 0, 1, 2],
[7, 9, 4, 1, 0, 5, 0, 6, 8],
[2, 0, 1, 4, 0, 0, 9, 5, 7],
[0, 0, 0, 2, 1, 0, 5, 0, 0],
[0, 5, 6, 3, 0, 0, 2, 4, 1],
[0, 1, 2, 5, 4, 0, 7, 3, 9],
[6, 3, 0, 8, 7, 4, 0, 0, 0],
[1, 0, 5, 6, 0, 2, 8, 0, 0],
[4, 2, 8, 9, 0, 1, 0, 7, 0]]
     
fixedLocations = [] 
for x in range(9):
    for y in range(9):
        if startState[y][x] != 0:
            fixedLocations.append(Location(x, y))

showState(startState)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)


Als nächstes baust du eine Funktion isValid(state) ein, die überprüft, ob ein bestimmter Spielzustand state die Spielregeln befolgt. Dies ist eine reine Knochenarbeit,  da du einfach die 9 Zeilen und 9 Spalten, sowie die 9 quadratischen Blöcke überprüfen musst. Das Resultat schreibst du in der Statusbar aus.

   

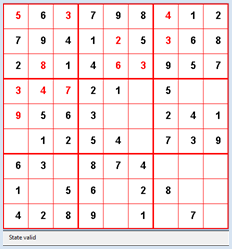
from gamegrid import *

def pressEvent(e):
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in fixedLocations:
        setStatusText("Location fixed")
        return
    xs = loc.x // 3
    ys = loc.y // 3
    x = loc.x % 3
    y = loc.y % 3
    value = startState[ys][xs][y][x]
    value = (value + 1)  % 10
    startState[ys][xs][y][x] = value
    showState(startState)
    if isValid(startState):
        setStatusText("State valid")
    else:
        setStatusText("Invalid state")

def showState(state):
    removeAllActors()
    for ys in range(3):
        for xs in range(3):
            for y in range(3):
                for x in range(3):
                    loc = Location(x + 3 * xs, y + 3 * ys)
                    value = state[ys][xs][y][x]
                    if  value != 0:
                        if loc in fixedLocations:
                            c = Color.black
                        else:
                            c = Color.red
                        digit = TextActor(str(value), c, Color.white, 
                                Font("Arial", Font.BOLD, 20))
                        addActorNoRefresh(digit, loc)
    refresh()

def isValid(state):
    # Check lines
    for ys in range(3):
        for y in range(3):
            line = []
            for xs in range(3):
                for x in range(3):
                    value = state[ys][xs][y][x]
                    if value > 0 and value in line:
                        return False
                    else:
                        line.append(value)    
    # Check rows
    for xs in range(3):
        for x in range(3):
            row = []
            for ys in range(3):
                for y in range(3):
                    value = state[ys][xs][y][x]
                    if value > 0 and value in row:
                        return False
                    else:
                        row.append(value)    

    # Check subgrids
    for ys in range(3):
        for xs in range(3):
            subgrid = state[ys][xs]
            square = []
            for y in range(3):
                for x in range(3):
                    value = subgrid[y][x]
                    if value > 0 and value in square:
                        return False
                    else:
                        square.append(value)
    return True

makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent)
show()
setTitle("Sudoku")
addStatusBar(30)
visited = []
setBgColor(Color.white)
getBg().setLineWidth(3)
getBg().setPaintColor(Color.red)
for x in range(4):
    getBg().drawLine(150 * x, 0, 150 * x, 450) 
for y in range(4):
    getBg().drawLine(0, 150 * y, 450, 150 * y) 

stateWiki = [[[[0, 3, 0], [0, 0, 0], [0, 0, 8]],
              [[0, 0, 0], [1, 9, 5], [0, 0, 0]],  
              [[0, 0, 0], [0, 0, 0], [0, 6, 0]]], 
             [[[8, 0, 0], [4, 0, 0], [0, 0, 0]],
              [[0, 6, 0], [8, 0, 0], [0, 2, 0]],
              [[0, 0, 0], [0, 0, 1], [0, 0, 0]]],
             [[[0, 6, 0], [0, 0, 0], [0, 0, 0]],
              [[0, 0, 0], [4, 1, 9], [0, 0, 0]],
              [[2, 8, 0], [0, 0, 5], [0, 7, 0]]]]   
startState = stateWiki

fixedLocations = [] 
for xs in range(3):
    for ys in range(3):
        for x in range(3):
            for y in range(3):
                if startState[ys][xs][y][x] != 0:
                    fixedLocations.append(Location(x + 3 * xs, y + 3 * ys))

showState(startState)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

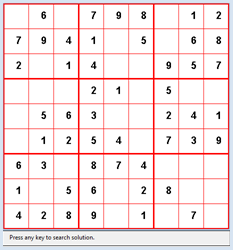
Für das Backtracking musst mit der Funktion getNeighbours(state) die Nachfolgeknoten eines Zustands bestimmen. Dabei wählst du mit getEmptyCell() eine leere Zelle aus und setzt dort der Reihe nach alle Zahlen ein, die zu einem legalen Spielzustand gehören. Mindestens eine davon wir sicher die richtige sein.

In getNeighbours(state) kopierst du zuerst die gegebene Zustandsliste in einen Clone, da du den übergegebenen Zustand nicht verändern darfst. Nachher füllst du die leere Zelle nacheinander mit den Zahlen 1 bis 9 und fügst Kopien der erlaubten Zustände in die Nachbarliste, die du zuletzt zurückgibst [mehr... Im Modul copy gibt es die Funktion deepcopy(), welche einen Clone erstellt.]

Die rekursive definierte Funktion search(), die das eigentliche Backtracking durchführt, kannst praktisch unverändert von anderen Backtracking-Problemen übernehmen. Du suchst hier nur nach einer einzigen Lösung und beendest mit dem Flag found den rekursiven Aufruf.



   

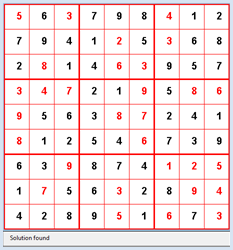
from gamegrid import *

def pressEvent(e):
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in fixedLocations:
        setStatusText("Location fixed")
        return
    x = loc.x
    y = loc.y
    value = startState[y][x]
    value = (value + 1)  % 10
    startState[y][x] = value
    showState(startState)
    if isValid(startState):
        setStatusText("State valid")
    else:
        setStatusText("Invalid state")

def getBlockValues(state, x, y):
    return [state[y][x], state[y][x + 1], state[y][x + 2], 
            state[y + 1][x], state[y + 1][x + 1], state[y + 1][x + 2],
            state[y + 2][x], state[y + 2][x + 1], state[ y + 2][x + 2]]
           
def showState(state):
    removeAllActors()
    for y in range(9):
        for x in range(9):
            loc = Location(x, y)
            value = state[y][x]
            if  value != 0:
                if loc in fixedLocations:
                    c = Color.black
                else:
                    c = Color.red
                digit = TextActor(str(value), c, Color.white, 
                        Font("Arial", Font.BOLD, 20))
                addActorNoRefresh(digit, loc)
    refresh()

def isValid(state):
    # Check lines
    for y in range(9):
        values = []
        for x in range(9):
            value = state[y][x]
            if value > 0 and value in values:
                return False
            else:
                values.append(value)    
    # Check rows
    for x in range(9):
        values = []
        for y in range(9):
            value = state[y][x]
            if value > 0 and value in values:
                return False
            else:
                values.append(value)    

    # Check blocks
    for yblock in range(3):
        for xblock in range(3):
            values = []
            li = getBlockValues(state, 3 * xblock, 3 * yblock)
            for value in li:
                if value > 0 and value in values:
                    return False
                else:
                    values.append(value)
    return True

def getEmptyCell(state):
    emptyCells = []
    for y in range(9):
        for x in range(9):
            if state[y][x] == 0:
                return [x, y]
    return []

def cloneState(state):
    li = []
    for y in range(9):
        line = []
        for x in range(9):
           line.append(state[y][x])
        li.append(line)
    return li
    
def getNeighbours(state):
    clone = cloneState(state)
    cell = getEmptyCell(state)
    validStates = []
    for value in range(1, 10):
        clone[cell[1]][cell[0]] = value
        if isValid(clone):
            validStates.append(cloneState(clone))
    return validStates

def search(state):
    global found, solution 
    if found:
        return
    visited.append(state)  # state marked as visited

    # Check for solution
    if getEmptyCell(state) == []:
        solution = state
        found = True
        return
        
    for neighbour in getNeighbours(state):
        if neighbour not in visited: # Check if already visited
            search(neighbour) # recursive call
    visited.pop() 
    
makeGameGrid(9, 9, 50, Color.red, False, mousePressed = pressEvent)
show()
setTitle("Sudoku")
addStatusBar(30)
visited = []
setBgColor(Color.white)
getBg().setLineWidth(3)
getBg().setPaintColor(Color.red)
for x in range(4):
    getBg().drawLine(150 * x, 0, 150 * x, 450) 
for y in range(4):
    getBg().drawLine(0, 150 * y, 450, 150 * y) 

startState = [ 
[0, 6, 0, 7, 9, 8, 0, 1, 2],
[7, 9, 4, 1, 0, 5, 0, 6, 8],
[2, 0, 1, 4, 0, 0, 9, 5, 7],
[0, 0, 0, 2, 1, 0, 5, 0, 0],
[0, 5, 6, 3, 0, 0, 2, 4, 1],
[0, 1, 2, 5, 4, 0, 7, 3, 9],
[6, 3, 0, 8, 7, 4, 0, 0, 0],
[1, 0, 5, 6, 0, 2, 8, 0, 0],
[4, 2, 8, 9, 0, 1, 0, 7, 0]]

fixedLocations = [] 
for x in range(9):
    for y in range(9):
        if startState[y][x] != 0:
            fixedLocations.append(Location(x, y))

showState(startState)
setStatusText("Press any key to search solution.")
getKeyCodeWait(True)
setStatusText("Searching. Please wait...")
found = False
solution = None
search(startState)
if solution != None:
    showState(solution)
    setStatusText("Solution found")
else:
    setStatusText("No solution")

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Du kannst auch Sudoku-Vorgaben verwenden, die du im Internet oder in einer Rätselecke gefunden hast. Wenn du genügend Geduld hast, so sollte dein Programm immer eine Lösung finden.

Man kann die Rechenzeit drastisch senken, falls man Lösungsstrategien in das Programm einbeziehst, die man auch bei der Lösung von Hand anwendet. Es bleibt dir überlassen, den Algorithmus mit solchen heuristischen Verfahren zu verbessern.

Das Lösungsverfahren lässt sich auch auf Sudoku-Vorgaben anwenden, die nicht-quadratische Blöcke aufweisen. Du musst dazu lediglich die Funktion getBlockValues() entsprechend anpassen.

 

 

DIE EIFERSÜCHTIGEN EHEMÄNNER

 

Bereits um 1613. hat der Mathematiker C. G. Bachet, Sieur de Méziriac eine Untersuchung mit dem Titel Problèmes plaisants et détectables qui se font par les nombres veröffentlicht, in dem er das Rätsel Les vilains maris jaloux wie folgt beschreibt:

"Trois maris jaloux se trouvent le soir avec leurs femmes au passage d'une rivière, et rencontrent un bateau sans batelier; le bateau est si petit, qu'il ne peut porter plus de deux personnes à la fois. On demande comment ces six personnes passeront de tel sorte qu'aucune femme ne demeure en la compagnie d'un ou de deux hommes, si son mari n'est présent, soit sur l'une des deux rives, soit sur le bateau." (Lit. Édouard Lucas, L'arithmétique amusante" 1885, reprint 2006)

  

Claude Gaspard Bachet de Méziriac (1581-1638) (© Wiki)

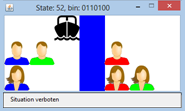
"Drei eifersüchtige Ehemänner befinden sich am Abend zusammen mit ihren Ehefrauen an einem Flussübergang, wo sie ein Boot ohne Bootsführer vorfinden. Das Boot ist so klein, dass darin nur zwei Personen Platz haben. Es stellt sich die Frage, wie die 6 Personen den Fluss überqueren können, ohne dass sich jemals eine der Frauen in Anwesenheit eines oder zwei Männer befindet, ohne dass ihr eigener Ehemann dabei ist, sei es auf der einen oder anderen Seite des Flusses, sei es im Boot."

Das Problem löst du wieder schrittweise und erstellst als erstes die Benutzeroberfläche, wobei sich ein GameGrid gut eignet, da man die Personen leicht durch Spritebilder veranschaulichen kann. Du fügst die GameGrid-Actors in ein unsichtbares Gitter der Grösse 7x3, damit du im Mittelstreifen den Fluss einzeichnen kannst. Da es nur wesentlich ist, ob sich eine Person links oder rechts vom Fluss befindet, ist als Datenstruktur eine Dualzahl geeignet, bei der jedes Bit zu einer bestimmten Person gehört. Der Bitwert 0 sagt, dass sich die Person links, der Wert 1, dass sie sich rechts vom Fluss befindet. Für das Boot verwendest du das Bit mit der höchsten Wertigkeit.

In der Simulation gibt es ein blaues, grünes und rotes Ehepaar, die du folgenden Stellen der Dualzahl zuordnest:

b6
b5
b4
b3
b2
b1
b0
boat
man_red
female_red
man_green
female_green
man_blue
female_blue

b0 ist das Bit mit der kleinsten Wertigkeit. Interpretierst du den Zustand im Dezimalsystem, so kommen also alle Zahlen zwischen 0 und 127 vor, d.h. es gibt 128 verschiedene Zustände.  

Es ist sehr zu empfehlen, dass du auch hier einen kleinen Umweg nimmst, damit du in einem Testprogramm die Kodierung der Zustände ausprobieren kannst. Mit einem Mausklick auf eine Person oder auf das Boot springt das Bild von der einen Seite auf die andere Seite des Flusses und der Zustand wird dezimal und binär in der Titelzeile ausgeschrieben.

  

Bereits hier baust du mit isStateAllowed(state) einen Test ein, ob die aktuelle Situation gemäss den Vorgaben legal ist. (Du könntest auch zuerst eine Vorversion ohne diesen Test erstellen.)

from gamegrid import *

def pressEvent(e):
    global state
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in left_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    if loc in right_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    state = 0
    for i in range(7):
        loc = right_locations[i]
        actor = getOneActorAt(loc)
        if actor != None:
            state += 2**(6 - i)
    showState(state)

def stateToString(state):
    return str(bin(state)[2:]).zfill(7)

def showState(state):
    sbin = stateToString(state)
    for i in range(7):
        if sbin[i] == "0":
           actors[i].setLocation(left_locations[i])
        else:
           actors[i].setLocation(right_locations[i])
    setTitle("State: " + str(state) + ", bin: " + stateToString(state)) 
    if isStateAllowed(state):
        setStatusText("Situation allowed")
    else:
        setStatusText("Situation not allowed")
    refresh()

def isStateAllowed(state):
    print(state)
    stateStr = stateToString(state)
    mred = stateStr[1] == "1"
    fred = stateStr[2] == "1"
    mgreen = stateStr[3] == "1"
    fgreen = stateStr[4] == "1"
    mblue = stateStr[5] == "1"
    fblue = stateStr[6] == "1"

    if mred and not fred or not mred and fred: # mred/fred not together
        if not fred and (not mgreen or not mblue) or fred and (mgreen or mblue):
            return False
    if mgreen and not fgreen or not mgreen and fgreen:#mgreen/fgreen not together
        if not fgreen and (not mred or not mblue) or fgreen and (mred or mblue):
            return False
    if mblue and not fblue or not mblue and fblue:  # mblue/fblue not together
        if not fblue and (not mred or not mgreen) or fblue and (mred or mgreen):
            return False
    return True   

makeGameGrid(7, 3, 50, None, False, mousePressed = pressEvent)
setBgColor(Color.white)
addStatusBar(30)        
show()
actors = [Actor("sprites/boat.png"), 
   Actor("sprites/man_0.png"), Actor("sprites/woman_0.png"),
   Actor("sprites/man_1.png"), Actor("sprites/woman_1.png"),
   Actor("sprites/man_2.png"), Actor("sprites/woman_2.png")]

left_locations =  [Location(2, 0), 
                   Location(2, 1), Location(2, 2), 
                   Location(1, 1), Location(1, 2), 
                   Location(0, 1), Location(0, 2)] 
right_locations = [Location(4, 0), 
                   Location(4, 1), Location(4, 2), 
                   Location(5, 1), Location(5, 2), 
                   Location(6, 1), Location(6, 2)] 

for i in range(7):
    addActorNoRefresh(actors[i], left_locations[i])
for i in range(3):    
   getBg().fillCell(Location(3, i), Color.blue)   
refresh()

startState = 0
showState(startState)

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

Als nächstes implementierst du wieder den Backtracking-Algorithmus, wie du ihn aus Kapitel 10.3. bestens kennst. Dabei muss du als erstes in getNeighbours(state) zu einem bestimmen Zustand alle möglichen Folgezustände bestimmen. Dabei gehst du so vor: Zuerst unterscheidest du, ob sich das Boot links (state < 64) oder rechts (state >=64) befindet. Dann bestimmst du in den Listen li_one und li_two alle Personen, die für einen Transfer als Einzelperson oder im Zweierteam in Frage kommen. Dabei musst du noch mit removeForbiddenTransfers() berücksichtigen, dass eine Frau wirklich nie mit einem fremden Mann im Boot sitzt.

In search() implementierst du das Backtracking in bekannter Form. Die Lösungen kopierst du in eine Liste solutions, auf die du nach Ende des Suchvorgangs zugreifen kannst, um die Lösungen zu untersuchen. Dabei schreibst du zuerst die Anzahl gefundener Lösungen aus und wählst dann die kürzeste aus, die du mit Tastenbetätigungen durchlaufen kannst.

from gamegrid import *
import itertools

def pressEvent(e): 
    global state
    loc = toLocationInGrid(e.getX(), e.getY())
    if loc in left_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    if loc in right_locations:
        actor = getOneActorAt(loc)
        if actor != None:
            x = 6 - actor.getX()
            y = actor.getY()
            actor.setLocation(Location(x, y))
    state = 0
    for i in range(7):
        loc = right_locations[i]
        actor = getOneActorAt(loc)
        if actor != None:
            state += 2**(6 - i)
    setTitle("State: " + str(state) + ", bin: " + stateToString(state)) 
    if isStateAllowed(state):
        setStatusText("Situation allowed")
    else:
        setStatusText("Situation not allowed")
    refresh()

def stateToString(state):
    return str(bin(state)[2:]).zfill(7)

def showState(state):
    sbin = stateToString(state)
    for i in range(7):
        if sbin[i] == "0":
           actors[i].setLocation(left_locations[i])
        else:
           actors[i].setLocation(right_locations[i])
    refresh()

def getTransferInfo(state1, state2):
    state1 = state1 & 63
    state2 = state2 & 63
    mod = state1 ^ state2
    passList = []
    for n in range(6):
        if mod % 2 == 1:
            if n // 2 == 0:
                couple = "blue"
            elif n // 2 == 1:
                couple = "green"
            elif n // 2 == 2:
                couple = "red"
            if n % 2 == 0:
               passList.append("f" + couple)
            else:
               passList.append("m" + couple)
        mod = mod // 2
    return passList

def getTransferSequence(solution):
    transferSequence = []
    oldState = solution[0]
    for state in solution[1:]:
        transferSequence.append(getTransferInfo(oldState, state))
        oldState = state
    return transferSequence

def isStateAllowed(state):
    stateStr = stateToString(state)
    mred = stateStr[1] == "1"
    fred = stateStr[2] == "1"
    mgreen = stateStr[3] == "1"
    fgreen = stateStr[4] == "1"
    mblue = stateStr[5] == "1"
    fblue = stateStr[6] == "1"

    if mred and not fred or not mred and fred:  # mred/fred not together
        if not fred and (not mgreen or not mblue) or fred and (mgreen or mblue):
            return False
    if mgreen and not fgreen or not mgreen and fgreen:#mgreen/fgreen not together
        if not fgreen and (not mred or not mblue) or fgreen and (mred or mblue):
            return False
    if mblue and not fblue or not mblue and fblue:  # mblue/fblue not together
        if not fblue and (not mred or not mgreen) or fblue and (mred or mgreen):
            return False
    return True

def removeForbiddenTransfers(li):
    forbiddenPairs = [(0, 3), (0, 5), (1, 2), (2, 5), (1, 4), (3, 4)]
    allowedPairs = []
    for pair in li:
        if pair not in forbiddenPairs:
            allowedPairs.append(pair)
    return allowedPairs  
        
def getNeighbours(state):
    neighbours = []
    li_one = []  # one person in boat
    bin = stateToString(state)
    if state < 64:  # boat at left
        for i in range(6):
            if bin[6 - i] == "0":
                li_one.append(i)
        li_two = list(itertools.combinations(li_one, 2)) #two persons in boat
        li_two = removeForbiddenTransfers(li_two)
    else: # boat at right
        for i in range(6):
            if bin[6 - i] == "1":
                li_one.append(i)
        li_two = list(itertools.combinations(li_one, 2))
        li_two = removeForbiddenTransfers(li_two)

    li_values = []
    if state < 64:  # boat at left, restrict to two persons transfer
        for li in li_two:
            li_values.append(2**li[0] + 2**li[1] + 64) 
    else:  # boat at right, one or two persons transfer
        for i in li_one:
            li_values.append(2**i + 64)
        for li in li_two:
            li_values.append(2**li[0] + 2**li[1] + 64) 
   
    for value in li_values:
        v = state ^ value
        if isStateAllowed(v):  # restrict to allowed states
            neighbours.append(v)
    return neighbours

def search(state):
    visited.append(state)  # state marked as visited

    # Check for solution
    if state == targetState:
        solutions.append(visited[:])
        
    for neighbour in getNeighbours(state):
        if neighbour not in visited: # Check if already visited
            search(neighbour) # recursive call
    visited.pop() 

nbSolution = 0             
makeGameGrid(7, 3, 50, None, False, mousePressed = pressEvent)
addStatusBar(30)
setBgColor(Color.white)
setTitle("Searching...")
show()
visited = []
actors = [Actor("sprites/boat.png"), 
   Actor("sprites/man_0.png"), Actor("sprites/woman_0.png"),
   Actor("sprites/man_1.png"), Actor("sprites/woman_1.png"),
   Actor("sprites/man_2.png"), Actor("sprites/woman_2.png")]

left_locations =  [Location(2, 0), 
                   Location(2, 1), Location(2, 2), 
                   Location(1, 1), Location(1, 2), 
                   Location(0, 1), Location(0, 2)] 
right_locations = [Location(4, 0), 
                   Location(4, 1), Location(4, 2), 
                   Location(5, 1), Location(5, 2), 
                   Location(6, 1), Location(6, 2)] 

for i in range(7):
    addActorNoRefresh(actors[i], left_locations[i])
for i in range(3):    
   getBg().fillCell(Location(3, i), Color.blue)   
refresh()

startState = 0
targetState = 127 
solutions = []
search(startState)

maxLength = 0
maxSolution = None
minLength = 100
minSolution = None
for solution in solutions:
    if len(solution) > maxLength:
        maxLength = len(solution)
        maxSolution = solution
    if len(solution) < minLength:
        minLength = len(solution)
        minSolution = solution
setStatusText("#Solutions: " + str(len(solutions)) + ", Min Length: " 
             + str(minLength) + ", Max Length: " + str(maxLength))

setTitle("Press key to cycle")
oldState = startState
for state in minSolution[1:]:
    getKeyCodeWait(True)
    showState(state)
    info = getTransferInfo(oldState, state)
    setTitle("#Transferred: " + str(info))
    oldState = state
setTitle("Done. #Boat Transfers: " + str((len(minSolution) - 1)))

Programmcode markieren (Ctrl+C kopieren, Ctrl+V einfügen)

 

 

MEMO

 

Rätsel dieser Art haben die Eigenschaft, dass man zum vornherein nicht weisst, ob sie keine, genau eine oder mehrere Lösungen haben. Dabei zeigt sich, dass es für uns Menschen viel einfacher ist, eine Lösung zu finden, als zu beweisen, dass es keine Lösung gibt. Für den Computer, der mit der Erschöpfenden Suche systematisch nach allen Lösungen sucht, ist das Aufsuchen aller Lösungen grundsätzlich kein Problem, ausser dass der Lösungsprozess sehr lange dauern kann. Dies ist wegen der kombinatorischen Explosion leider schon bei relativ einfachen Spielanlagen der Fall, sodass wir auch hier wieder an Grenzen des Computereinsatzes stossen.
 
Es ist interessant, dass bereits Bachet die Minimallösung mit 11 Überfahrten publizierte, die auch dein Computerprogramm findet. Dabei hat er von Überfahrt zu Überfahrt so geschickt argumentiert, dass der Lösungsgang evident erscheint. Ob er die Lösung allerdings zuerst doch nach der Methode von "Versuch und Irrtum" gefunden und erst nachträglich die Argumente dazu aufgeschrieben hat, bleibe dahingestellt.

 

 

AUFGABEN

 

1.


Suche ein Lösung für das folgende X-Sudoku, bei dem auch auf den beiden Hauptdiagonalen die 9 Zahlen genau einmal vorkommen müssen.
2.

Zeige, dass es keine Lösung des Problems der "Eifersüchtigen Ehemänner" gibt, falls man nur Einpersonentransfers vom rechten zum linken Ufer zulässt.